வீடு→வீட்டு உபயோகப் பொருட்கள்→ஒரு முக்கோணவியல் ஃபோரியர் தொடராக காலச் சார்பின் விரிவாக்கம். ஃபோரியர் தொடர்: அறிவியலின் வளர்ச்சியில் கணித பொறிமுறையின் வரலாறு மற்றும் தாக்கம்

ஒரு முக்கோணவியல் ஃபோரியர் தொடராக காலச் சார்பின் விரிவாக்கம். ஃபோரியர் தொடர்: அறிவியலின் வளர்ச்சியில் கணித பொறிமுறையின் வரலாறு மற்றும் தாக்கம்

ஃபோரியர் தொடர்கள் என்பது ஒரு தொடர் வடிவத்தில் ஒரு குறிப்பிட்ட காலப்பகுதியுடன் தன்னிச்சையான செயல்பாட்டின் பிரதிநிதித்துவம் ஆகும். IN பொதுவான பார்வை இந்த முடிவுஆர்த்தோகனல் அடிப்படையில் ஒரு தனிமத்தின் சிதைவு என்று அழைக்கப்படுகிறது. ஃபோரியர் தொடரில் செயல்பாடுகளை விரிவுபடுத்துவது, ஒருங்கிணைப்பு, வேறுபாடு மற்றும் வாதம் மற்றும் மாற்றத்தின் மூலம் வெளிப்பாடுகளை மாற்றும் போது இந்த மாற்றத்தின் பண்புகள் காரணமாக பல்வேறு சிக்கல்களைத் தீர்ப்பதற்கான மிகவும் சக்திவாய்ந்த கருவியாகும்.

உயர் கணிதம் மற்றும் பிரெஞ்சு விஞ்ஞானி ஃபோரியரின் படைப்புகள் பற்றி அறிந்திராத ஒரு நபர், இந்த "தொடர்கள்" என்ன, அவை என்ன தேவை என்பதை பெரும்பாலும் புரிந்து கொள்ள மாட்டார். இதற்கிடையில், இந்த மாற்றம் நம் வாழ்வில் மிகவும் ஒருங்கிணைக்கப்பட்டுள்ளது. இது கணிதவியலாளர்களால் மட்டுமல்ல, இயற்பியலாளர்கள், வேதியியலாளர்கள், மருத்துவர்கள், வானியலாளர்கள், நிலநடுக்கவியலாளர்கள், கடல் ஆய்வாளர்கள் மற்றும் பலரால் பயன்படுத்தப்படுகிறது. அதன் காலத்திற்கு முந்திய ஒரு கண்டுபிடிப்பைச் செய்த சிறந்த பிரெஞ்சு விஞ்ஞானியின் படைப்புகளையும் நாம் கூர்ந்து கவனிப்போம்.

மனிதன் மற்றும் ஃபோரியர் மாற்றம்

ஃபோரியர் தொடர் முறைகளில் ஒன்றாகும் (பகுப்பாய்வு மற்றும் பிறவற்றுடன்) இந்த செயல்முறை ஒரு நபர் ஒலியைக் கேட்கும் ஒவ்வொரு முறையும் நிகழ்கிறது. நமது காது தானாகவே ஒரு மீள் ஊடகத்தில் உள்ள அடிப்படைத் துகள்களை வெவ்வேறு உயரங்களின் டோன்களுக்கான தொடர்ச்சியான தொகுதி அளவுகளின் வரிசைகளாக (ஸ்பெக்ட்ரம் சேர்த்து) மாற்றுகிறது. அடுத்து, மூளை இந்தத் தரவை நமக்கு நன்கு தெரிந்த ஒலிகளாக மாற்றுகிறது. இவை அனைத்தும் நம் ஆசை அல்லது நனவுக்கு வெளியே நிகழ்கின்றன, ஆனால் இந்த செயல்முறைகளைப் புரிந்து கொள்ள, உயர் கணிதத்தைப் படிக்க பல ஆண்டுகள் ஆகும்.

ஃபோரியர் மாற்றம் பற்றி மேலும்

ஃபோரியர் மாற்றத்தை பகுப்பாய்வு, எண் மற்றும் பிற முறைகளைப் பயன்படுத்தி மேற்கொள்ளலாம். ஃபோரியர் தொடர் என்பது கடல் அலைகள் மற்றும் ஒளி அலைகள் முதல் சூரிய (மற்றும் பிற வானியல் பொருள்கள்) செயல்பாட்டின் சுழற்சிகள் வரை எந்த ஊசலாட்ட செயல்முறைகளையும் சிதைக்கும் எண்ணியல் முறையைக் குறிக்கிறது. இந்த கணித நுட்பங்களைப் பயன்படுத்தி, நீங்கள் செயல்பாடுகளை பகுப்பாய்வு செய்யலாம், எந்த ஊசலாட்ட செயல்முறைகளையும் சைனூசாய்டல் கூறுகளின் வரிசையாகக் குறிக்கும், அவை குறைந்தபட்சம் முதல் அதிகபட்சம் மற்றும் பின்னோக்கி நகரும். ஃபோரியர் உருமாற்றம் என்பது ஒரு குறிப்பிட்ட அதிர்வெண்ணுடன் தொடர்புடைய சைனூசாய்டுகளின் கட்டம் மற்றும் வீச்சு ஆகியவற்றை விவரிக்கும் ஒரு செயல்பாடாகும். இந்த செயல்முறை மிகவும் தீர்க்க பயன்படுத்தப்படலாம் சிக்கலான சமன்பாடுகள், இது வெப்ப, ஒளி அல்லது செல்வாக்கின் கீழ் எழும் மாறும் செயல்முறைகளை விவரிக்கிறது மின் ஆற்றல். மேலும், ஃபோரியர் தொடர்கள் சிக்கலான அலைவு சமிக்ஞைகளில் நிலையான கூறுகளை தனிமைப்படுத்துவதை சாத்தியமாக்குகிறது, இது மருத்துவம், வேதியியல் மற்றும் வானியல் ஆகியவற்றில் பெறப்பட்ட சோதனை அவதானிப்புகளை சரியாக விளக்குகிறது.

வரலாற்று பின்னணி

இந்த கோட்பாட்டின் ஸ்தாபக தந்தை பிரெஞ்சு கணிதவியலாளர் ஜீன் பாப்டிஸ்ட் ஜோசப் ஃபோரியர் ஆவார். இந்த மாற்றத்திற்கு பின்னர் அவர் பெயரிடப்பட்டது. ஆரம்பத்தில், விஞ்ஞானி தனது முறையைப் பயன்படுத்தி வெப்ப கடத்துத்திறனின் வழிமுறைகளைப் படிக்கவும் விளக்கவும் பயன்படுத்தினார் - வெப்பத்தின் பரவல் திடப்பொருட்கள். ஆரம்ப ஒழுங்கற்ற விநியோகத்தை எளிய சைனூசாய்டுகளாக சிதைக்க முடியும் என்று ஃபோரியர் பரிந்துரைத்தார், அவை ஒவ்வொன்றும் அதன் சொந்த வெப்பநிலை குறைந்தபட்சம் மற்றும் அதிகபட்சம், அத்துடன் அதன் சொந்த கட்டம் ஆகியவற்றைக் கொண்டிருக்கும். இந்த வழக்கில், அத்தகைய ஒவ்வொரு கூறுகளும் குறைந்தபட்சம் அதிகபட்சம் மற்றும் பின் அளவிடப்படும். வளைவின் மேல் மற்றும் கீழ் சிகரங்களையும், ஒவ்வொரு ஹார்மோனிக்கின் கட்டத்தையும் விவரிக்கும் கணிதச் செயல்பாடு, வெப்பநிலை விநியோக வெளிப்பாட்டின் ஃபோரியர் மாற்றம் என்று அழைக்கப்படுகிறது. கோட்பாட்டின் ஆசிரியர் ஒன்றிணைத்தார் பொது செயல்பாடுவிநியோகம், இது கணித ரீதியாக விவரிக்க கடினமாக உள்ளது, கோசைன் மற்றும் சைன் ஆகியவற்றின் மிகவும் வசதியான தொடர், இது ஒன்றாக அசல் விநியோகத்தை அளிக்கிறது.

மாற்றத்தின் கொள்கை மற்றும் சமகாலத்தவர்களின் கருத்துக்கள்

விஞ்ஞானியின் சமகாலத்தவர்கள் - பத்தொன்பதாம் நூற்றாண்டின் தொடக்கத்தில் முன்னணி கணிதவியலாளர்கள் - இந்த கோட்பாட்டை ஏற்கவில்லை. ஒரு நேர்கோடு அல்லது இடைவிடாத வளைவை விவரிக்கும் ஒரு இடைவிடாத செயல்பாடு, தொடர்ச்சியாக இருக்கும் சைனூசாய்டல் வெளிப்பாடுகளின் கூட்டுத்தொகையாகக் குறிப்பிடப்படலாம் என்று ஃபோரியரின் வலியுறுத்தல் முக்கிய ஆட்சேபனையாகும். எடுத்துக்காட்டாக, ஹெவிசைட் படியைக் கவனியுங்கள்: அதன் மதிப்பு இடைநிறுத்தத்தின் இடதுபுறத்தில் பூஜ்ஜியமாகவும், ஒன்று வலதுபுறமாகவும் இருக்கும். இந்த செயல்பாடுபோதையை விவரிக்கிறது மின்சாரம்சுற்று மூடப்படும் போது ஒரு தற்காலிக மாறியிலிருந்து. அந்த நேரத்தில் கோட்பாட்டின் சமகாலத்தவர்கள் இதேபோன்ற சூழ்நிலையை எதிர்கொண்டதில்லை, அங்கு ஒரு தொடர்ச்சியற்ற வெளிப்பாடு தொடர்ச்சியான, சாதாரண செயல்பாடுகளான அதிவேக, சைன், நேரியல் அல்லது இருபடி ஆகியவற்றின் கலவையால் விவரிக்கப்படும்.

ஃபோரியரின் கோட்பாடு பற்றி பிரெஞ்சு கணிதவியலாளர்களை குழப்பியது எது?

எல்லாவற்றிற்கும் மேலாக, கணிதவியலாளர் தனது கூற்றுகளில் சரியாக இருந்தால், எல்லையற்ற முக்கோணவியல் ஃபோரியர் தொடரைச் சுருக்கி, படி வெளிப்பாட்டின் துல்லியமான பிரதிநிதித்துவத்தைப் பெறலாம், அது பல ஒத்த படிகளைக் கொண்டிருந்தாலும் கூட. பத்தொன்பதாம் நூற்றாண்டின் தொடக்கத்தில், அத்தகைய அறிக்கை அபத்தமானது. ஆனால் அனைத்து சந்தேகங்கள் இருந்தபோதிலும், பல கணிதவியலாளர்கள் இந்த நிகழ்வின் ஆய்வின் நோக்கத்தை விரிவுபடுத்தினர், வெப்ப கடத்துத்திறன் ஆய்வுக்கு அப்பால் அதை எடுத்துக் கொண்டனர். இருப்பினும், பெரும்பாலான விஞ்ஞானிகள் கேள்வியால் தொடர்ந்து துன்புறுத்தப்பட்டனர்: "ஒரு சைனூசாய்டல் தொடரின் கூட்டுத்தொகை இடைவிடாத செயல்பாட்டின் சரியான மதிப்புடன் ஒன்றிணைக்க முடியுமா?"

ஃபோரியர் தொடரின் ஒருங்கிணைப்பு: ஒரு எடுத்துக்காட்டு

எல்லையற்ற எண்களைத் தொகுக்க வேண்டியிருக்கும் போதெல்லாம் ஒருங்கிணைவு பற்றிய கேள்வி எழுகிறது. இந்த நிகழ்வைப் புரிந்து கொள்ள, ஒரு உன்னதமான உதாரணத்தைக் கவனியுங்கள். ஒவ்வொரு அடுத்த படியும் முந்தையதை விட பாதி அளவு இருந்தால் நீங்கள் எப்போதாவது சுவரை அடைய முடியுமா? நீங்கள் இலக்கில் இருந்து இரண்டு மீட்டர் இருக்கிறீர்கள் என்று வைத்துக்கொள்வோம், முதல் படி உங்களை பாதிக்கு அழைத்துச் செல்கிறது, அடுத்தது உங்களை முக்கால்வாசி மார்க்கிற்கு அழைத்துச் செல்கிறது, ஐந்தாவதுக்குப் பிறகு நீங்கள் கிட்டத்தட்ட 97 சதவீதத்தை கடந்துவிட்டீர்கள். எவ்வாறாயினும், நீங்கள் எத்தனை படிகள் எடுத்தாலும், கடுமையான கணித அர்த்தத்தில் நீங்கள் விரும்பிய இலக்கை அடைய முடியாது. எண் கணக்கீடுகளைப் பயன்படுத்தி, கொடுக்கப்பட்ட தூரத்தை நெருங்குவது இறுதியில் சாத்தியம் என்பதை நிரூபிக்க முடியும். இந்த ஆதாரம் ஒரு பாதி, நான்கில் ஒரு பங்கு போன்றவற்றின் கூட்டுத்தொகை ஒருமைப்பாட்டிற்குச் செல்லும் என்பதை நிரூபிப்பதற்குச் சமம்.

கன்வெர்ஜென்ஸ் கேள்வி: இரண்டாவது வருகை, அல்லது லார்ட் கெல்வின் சாதனம்

திரும்பத் திரும்ப இந்த கேள்விபத்தொன்பதாம் நூற்றாண்டின் இறுதியில் உயர்ந்தது, அவர்கள் ஃபோரியர் தொடரைப் பயன்படுத்தி அலைகளின் தீவிரம் மற்றும் ஓட்டம் ஆகியவற்றைக் கணிக்க முயன்றனர். இந்த நேரத்தில் கெல்வின் பிரபு இருந்தார் சாதனம் கண்டுபிடிக்கப்பட்டது, இது ஒரு அனலாக் கம்ப்யூட்டிங் சாதனமாகும், இது இராணுவ மற்றும் வணிக கடல் மாலுமிகள் இதைக் கண்காணிக்க அனுமதித்தது இயற்கை நிகழ்வு. இந்த பொறிமுறையானது அலை உயரங்கள் மற்றும் தொடர்புடைய நேரப் புள்ளிகளின் அட்டவணையில் இருந்து கட்டங்கள் மற்றும் வீச்சுகளின் தொகுப்பைத் தீர்மானித்தது, ஆண்டு முழுவதும் கொடுக்கப்பட்ட துறைமுகத்தில் கவனமாக அளவிடப்படுகிறது. ஒவ்வொரு அளவுருவும் அலை உயர வெளிப்பாட்டின் சைனூசாய்டல் கூறு மற்றும் வழக்கமான கூறுகளில் ஒன்றாகும். கெல்வின் பிரபுவின் கணக்கீட்டு கருவியில் அளவீடுகள் கொடுக்கப்பட்டன, இது அடுத்த ஆண்டுக்கான நேரத்தின் செயல்பாடாக நீரின் உயரத்தை கணிக்கும் ஒரு வளைவை ஒருங்கிணைத்தது. மிக விரைவில் உலகின் அனைத்து துறைமுகங்களுக்கும் இதேபோன்ற வளைவுகள் வரையப்பட்டன.

ஒரு இடைவிடாத செயல்பாட்டால் செயல்முறை சீர்குலைந்தால் என்ன செய்வது?

அந்த நேரத்தில் ஒரு அலை அலை கணிப்பு கருவி இருப்பது தெளிவாகத் தெரிந்தது ஒரு பெரிய எண்கணக்கு கூறுகள் கணக்கிட முடியும் பெரிய எண்ணிக்கைகட்டங்கள் மற்றும் வீச்சுகள் மற்றும் பலவற்றை வழங்குகின்றன துல்லியமான கணிப்புகள். இருப்பினும், ஒருங்கிணைக்கப்பட வேண்டிய அலை வெளிப்பாடு ஒரு கூர்மையான தாவலைக் கொண்டிருக்கும் சந்தர்ப்பங்களில் இந்த முறை கவனிக்கப்படவில்லை என்று மாறியது, அதாவது அது இடைவிடாது. நேரத் தருணங்களின் அட்டவணையிலிருந்து தரவு சாதனத்தில் உள்ளிடப்பட்டால், அது பல ஃபோரியர் குணகங்களைக் கணக்கிடுகிறது. அசல் செயல்பாடு சைனூசாய்டல் கூறுகளுக்கு நன்றி மீட்டமைக்கப்படுகிறது (கண்டுபிடிக்கப்பட்ட குணகங்களுக்கு ஏற்ப). அசல் மற்றும் புனரமைக்கப்பட்ட வெளிப்பாட்டிற்கு இடையிலான முரண்பாட்டை எந்த புள்ளியிலும் அளவிட முடியும். மீண்டும் மீண்டும் கணக்கீடுகள் மற்றும் ஒப்பீடுகளை மேற்கொள்ளும்போது, மிகப்பெரிய பிழையின் மதிப்பு குறையாது என்பது தெளிவாகிறது. இருப்பினும், அவை இடைநிறுத்தப் புள்ளியுடன் தொடர்புடைய பகுதியில் உள்ளூர்மயமாக்கப்படுகின்றன, மேலும் வேறு எந்த புள்ளியிலும் அவை பூஜ்ஜியமாக இருக்கும். 1899 ஆம் ஆண்டில், இந்த முடிவை யேல் பல்கலைக்கழகத்தின் ஜோசுவா வில்லார்ட் கிப்ஸ் கோட்பாட்டளவில் உறுதிப்படுத்தினார்.

ஃபோரியர் தொடரின் ஒருங்கிணைப்பு மற்றும் பொதுவாக கணிதத்தின் வளர்ச்சி

ஃபோரியர் பகுப்பாய்வு ஒரு குறிப்பிட்ட இடைவெளியில் எண்ணற்ற ஸ்பைக்குகளைக் கொண்ட வெளிப்பாடுகளுக்குப் பொருந்தாது. பொதுவாக, ஃபோரியர் தொடர், அசல் செயல்பாடு உண்மையான உடல் அளவீட்டின் விளைவாக குறிப்பிடப்பட்டால், எப்போதும் ஒன்றிணைகிறது. குறிப்பிட்ட வகை செயல்பாடுகளுக்கான இந்த செயல்முறையின் ஒருங்கிணைப்பு பற்றிய கேள்விகள் கணிதத்தில் புதிய கிளைகள் தோன்றுவதற்கு வழிவகுத்தது, எடுத்துக்காட்டாக, பொதுவான செயல்பாடுகளின் கோட்பாடு. அவர் எல். ஸ்வார்ட்ஸ், ஜே. மிகுசின்ஸ்கி மற்றும் ஜே. டெம்பிள் போன்ற பெயர்களுடன் தொடர்புடையவர். இந்த கோட்பாட்டின் கட்டமைப்பிற்குள், ஒரு தெளிவான மற்றும் துல்லியமான கோட்பாட்டு அடிப்படைடைராக் டெல்டா செயல்பாடு (இது ஒரு புள்ளியின் எல்லையற்ற சுற்றுப்புறத்தில் குவிந்துள்ள ஒரு பகுதியின் பகுதியை விவரிக்கிறது) மற்றும் ஹெவிசைட் "படி" போன்ற வெளிப்பாடுகளின் கீழ். இந்த வேலைக்கு நன்றி, ஃபோரியர் தொடர் சமன்பாடுகள் மற்றும் உள்ளுணர்வு கருத்துகளை உள்ளடக்கிய சிக்கல்களைத் தீர்ப்பதற்குப் பொருந்தும்: புள்ளி கட்டணம், புள்ளி நிறை, காந்த இருமுனைகள் மற்றும் ஒரு கற்றை மீது செறிவூட்டப்பட்ட சுமை.

ஃபோரியர் முறை

ஃபோரியர் தொடர், குறுக்கீடு கொள்கைகளுக்கு இணங்க, விரிவாக்கத்துடன் தொடங்குகிறது சிக்கலான வடிவங்கள்எளிமையானவர்களுக்கு. எடுத்துக்காட்டாக, வெப்ப-இன்சுலேடிங் பொருட்களால் செய்யப்பட்ட பல்வேறு தடைகள் வழியாக வெப்ப ஓட்டத்தில் ஏற்படும் மாற்றம் விளக்கப்படுகிறது. ஒழுங்கற்ற வடிவம்அல்லது பூமியின் மேற்பரப்பில் ஏற்படும் மாற்றம் - பூகம்பம், சுற்றுப்பாதையில் மாற்றம் வான உடல்- கிரகங்களின் தாக்கம். ஒரு விதியாக, எளிய கிளாசிக்கல் அமைப்புகளை விவரிக்கும் இத்தகைய சமன்பாடுகள் ஒவ்வொரு தனி அலைக்கும் எளிதாக தீர்க்கப்படும். ஃபோரியர் அதைக் காட்டினார் எளிய தீர்வுகள்மேலும் சிக்கலான பிரச்சனைகளுக்கான தீர்வுகளைப் பெறவும் சுருக்கமாகச் சொல்லலாம். கணித அடிப்படையில், ஃபோரியர் தொடர் என்பது ஹார்மோனிக்ஸ் - கொசைன் மற்றும் சைன் ஆகியவற்றின் கூட்டுத்தொகையாக வெளிப்பாட்டைக் குறிக்கும் ஒரு நுட்பமாகும். அதனால் தான் இந்த பகுப்பாய்வுஹார்மோனிக் பகுப்பாய்வு என்றும் அழைக்கப்படுகிறது.

ஃபோரியர் தொடர் - "கணினி யுகத்திற்கு" முன் ஒரு சிறந்த நுட்பம்

கணினி தொழில்நுட்பத்தை உருவாக்குவதற்கு முன்பு, நமது உலகின் அலை இயல்புடன் பணிபுரியும் போது விஞ்ஞானிகளின் ஆயுதக் களஞ்சியத்தில் ஃபோரியர் முறை சிறந்த ஆயுதமாக இருந்தது. சிக்கலான வடிவத்தில் உள்ள ஃபோரியர் தொடர் எளிய சிக்கல்களை மட்டும் தீர்க்க உதவுகிறது நேரடி விண்ணப்பம்நியூட்டனின் இயக்கவியல் விதிகள், ஆனால் அடிப்படை சமன்பாடுகள். பத்தொன்பதாம் நூற்றாண்டில் நியூட்டனின் அறிவியலின் பெரும்பாலான கண்டுபிடிப்புகள் ஃபோரியரின் நுட்பத்தால் மட்டுமே சாத்தியமானது.

இன்று ஃபோரியர் தொடர்

கணினிகளின் வளர்ச்சியுடன், ஃபோரியர் உருமாற்றங்கள் ஒரு தரமான நிலைக்கு உயர்ந்துள்ளன புதிய நிலை. இந்த நுட்பம்அறிவியல் மற்றும் தொழில்நுட்பத்தின் கிட்டத்தட்ட அனைத்து துறைகளிலும் உறுதியாக நிறுவப்பட்டது. ஒரு உதாரணம் டிஜிட்டல் ஆடியோ மற்றும் வீடியோ. பத்தொன்பதாம் நூற்றாண்டின் தொடக்கத்தில் ஒரு பிரெஞ்சு கணிதவியலாளரால் உருவாக்கப்பட்ட ஒரு கோட்பாட்டின் காரணமாக மட்டுமே அதன் செயல்படுத்தல் சாத்தியமானது. எனவே, ஃபோரியர் தொடர் ஒரு சிக்கலான வடிவத்தில் விண்வெளி ஆய்வில் ஒரு முன்னேற்றத்தை ஏற்படுத்தியது. கூடுதலாக, இது குறைக்கடத்தி பொருட்கள் மற்றும் பிளாஸ்மா, நுண்ணலை ஒலியியல், கடல்சார்வியல், ரேடார் மற்றும் நில அதிர்வு ஆகியவற்றின் இயற்பியல் ஆய்வில் தாக்கத்தை ஏற்படுத்தியது.

முக்கோணவியல் ஃபோரியர் தொடர்

கணிதத்தில், ஃபோரியர் தொடர் என்பது தன்னிச்சையான தன்மையைக் குறிக்கும் ஒரு வழியாகும் சிக்கலான செயல்பாடுகள்எளிமையானவைகளின் கூட்டுத்தொகை. பொதுவான சந்தர்ப்பங்களில், அத்தகைய வெளிப்பாடுகளின் எண்ணிக்கை எல்லையற்றதாக இருக்கலாம். மேலும், கணக்கீட்டில் அவற்றின் எண்ணிக்கை எவ்வளவு கணக்கில் எடுத்துக் கொள்ளப்படுகிறதோ, அவ்வளவு துல்லியமானது இறுதி முடிவு. பெரும்பாலும், கோசைன் அல்லது சைனின் முக்கோணவியல் செயல்பாடுகள் எளிமையானவையாகப் பயன்படுத்தப்படுகின்றன. இந்த வழக்கில், ஃபோரியர் தொடர் முக்கோணவியல் என்று அழைக்கப்படுகிறது, மேலும் அத்தகைய வெளிப்பாடுகளின் தீர்வு ஹார்மோனிக் விரிவாக்கம் என்று அழைக்கப்படுகிறது. இந்த முறை விளையாடுகிறது முக்கிய பங்குகணிதத்தில். முதலில், முக்கோணவியல் தொடர் செயல்பாடுகளை சித்தரிப்பதற்கும் படிப்பதற்கும் ஒரு வழிமுறையை வழங்குகிறது, இது கோட்பாட்டின் முக்கிய கருவியாகும். கூடுதலாக, இது கணித இயற்பியலில் பல சிக்கல்களைத் தீர்க்க உங்களை அனுமதிக்கிறது. இறுதியாக, இந்த கோட்பாடு கணித அறிவியலின் பல முக்கியமான கிளைகளின் வளர்ச்சிக்கு பங்களித்தது (ஒருங்கிணைந்த கோட்பாடு, காலச் செயல்பாடுகளின் கோட்பாடு). கூடுதலாக, இது ஒரு உண்மையான மாறியின் பின்வரும் செயல்பாடுகளின் வளர்ச்சிக்கான தொடக்க புள்ளியாக செயல்பட்டது, மேலும் ஹார்மோனிக் பகுப்பாய்விற்கு அடித்தளத்தை அமைத்தது.

காலம் 2π உடன் காலமுறை செயல்பாடுகளின் ஃபோரியர் தொடர்.

ஃபோரியர் தொடர், காலச் செயல்பாடுகளைக் கூறுகளாகச் சிதைப்பதன் மூலம் அவற்றைப் படிக்க அனுமதிக்கிறது. மாற்று நீரோட்டங்கள்மற்றும் மன அழுத்தம், இடப்பெயர்ச்சி, வேகம் மற்றும் கிராங்க் பொறிமுறைகளின் முடுக்கம் மற்றும் ஒலி அலைகள் ஆகியவை பொதுவானவை நடைமுறை உதாரணங்கள்பொறியியல் கணக்கீடுகளில் காலமுறை செயல்பாடுகளின் பயன்பாடு.

ஃபோரியர் தொடர் விரிவாக்கம் என்பது அனைவரும் கொண்டிருக்கும் அனுமானத்தின் அடிப்படையில் அமைந்துள்ளது நடைமுறை முக்கியத்துவம்இடைவெளியில் உள்ள செயல்பாடுகள் -π ≤x≤ π ஒருமுகமான முக்கோணவியல் தொடர் வடிவத்தில் வெளிப்படுத்தப்படலாம் (ஒரு தொடர் அதன் சொற்களால் ஆன பகுதித் தொகைகளின் வரிசை ஒன்றிணைந்தால் ஒன்றிணைந்ததாகக் கருதப்படுகிறது):

sinx மற்றும் cosx கூட்டுத்தொகை மூலம் நிலையான (=சாதாரண) குறியீடு

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

இதில் a o, a 1,a 2,...,b 1,b 2,.. உண்மையான மாறிலிகள், அதாவது.

குணகங்கள் -π முதல் π வரையிலான வரம்பிற்கு எங்கே ஃபோரியர் தொடர்சூத்திரங்களைப் பயன்படுத்தி கணக்கிடப்படுகிறது:

குணகங்கள் a o , a n மற்றும் b n என்று அழைக்கப்படுகின்றன ஃபோரியர் குணகங்கள், மற்றும் அவை கண்டுபிடிக்கப்பட்டால், தொடர் (1) அழைக்கப்படுகிறது ஃபோரியருக்கு அருகில், f(x) சார்புடன் தொடர்புடையது. தொடர் (1), சொல் (a 1 cosx+b 1 sinx) முதல் அல்லது அடிப்படை இசைவு,

தொடரை எழுத மற்றொரு வழி acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

ஒரு o என்பது 1 =(a 1 2 +b 1 2) 1/2 உடன், n =(a n 2 +b n 2) 1/2 - பல்வேறு கூறுகளின் வீச்சுகள் மற்றும் n = arctg க்கு சமம் a n /b n.

தொடர் (1)க்கான சொல் (a 1 cosx+b 1 sinx) அல்லது c 1 sin(x+α 1) முதல் அல்லது அடிப்படை இசைவு,(a 2 cos2x+b 2 sin2x) அல்லது c 2 sin(2x+α 2) அழைக்கப்படுகிறது இரண்டாவது ஹார்மோனிக்மற்றும் பல.

ஒரு சிக்கலான சிக்னலை துல்லியமாக பிரதிநிதித்துவப்படுத்த பொதுவாக எண்ணற்ற சொற்கள் தேவை. இருப்பினும், பல நடைமுறைச் சிக்கல்களில் முதல் சில சொற்களை மட்டும் கருத்தில் கொண்டால் போதுமானது.

காலம் 2π உடன் காலமுறை அல்லாத செயல்பாடுகளின் ஃபோரியர் தொடர்.

காலமுறை அல்லாத செயல்பாடுகளின் விரிவாக்கம்.

f(x) சார்பு கால இடைவெளியில் இல்லாததாக இருந்தால், அதை x இன் அனைத்து மதிப்புகளுக்கும் ஃபோரியர் தொடராக விரிவாக்க முடியாது என்று அர்த்தம். இருப்பினும், 2π அகலத்தின் எந்த வரம்பிலும் ஒரு செயல்பாட்டைக் குறிக்கும் ஃபோரியர் தொடரை வரையறுக்க முடியும்.

குறிப்பிட்ட வரம்பிற்குள் f(x) இன் மதிப்புகளைத் தேர்ந்தெடுத்து, 2π இடைவெளியில் அந்த வரம்பிற்கு வெளியே அவற்றை மீண்டும் செய்வதன் மூலம் ஒரு புதிய செயல்பாட்டை உருவாக்க முடியும். புதிய சார்பு காலம் 2π உடன் குறிப்பிட்ட கால இடைவெளியில் இருப்பதால், அதை x இன் அனைத்து மதிப்புகளுக்கும் ஃபோரியர் தொடராக விரிவாக்கலாம். எடுத்துக்காட்டாக, f(x)=x சார்பு காலநிலை அல்ல. இருப்பினும், o இலிருந்து 2π வரையிலான இடைவெளியில் அதை ஃபோரியர் தொடராக விரிவுபடுத்துவது அவசியமானால், இந்த இடைவெளிக்கு வெளியே 2π காலத்துடன் கூடிய காலச் செயல்பாடு கட்டமைக்கப்படுகிறது (கீழே உள்ள படத்தில் காட்டப்பட்டுள்ளது).

f(x)=x போன்ற காலச் சார்பற்ற செயல்பாடுகளுக்கு, ஃபோரியர் தொடரின் கூட்டுத்தொகையானது, கொடுக்கப்பட்ட வரம்பில் உள்ள அனைத்து புள்ளிகளிலும் f(x) இன் மதிப்புக்கு சமமாக இருக்கும், ஆனால் புள்ளிகளுக்கான f(x) க்கு சமமாக இருக்காது. எல்லைக்கு வெளியே. 2π வரம்பில் காலமுறை அல்லாத செயல்பாட்டின் ஃபோரியர் தொடரைக் கண்டறிய, ஃபோரியர் குணகங்களின் அதே சூத்திரம் பயன்படுத்தப்படுகிறது.

சம மற்றும் ஒற்றைப்படை செயல்பாடுகள்.

y=f(x) செயல்பாட்டைச் சொல்கிறார்கள் கூட, x இன் அனைத்து மதிப்புகளுக்கும் f(-x)=f(x) என்றால். சமச் சார்புகளின் வரைபடங்கள் எப்போதும் y- அச்சைப் பற்றி சமச்சீராக இருக்கும் (அதாவது, அவை கண்ணாடிப் படங்கள்). சம செயல்பாடுகளுக்கு இரண்டு எடுத்துக்காட்டுகள்: y=x2 மற்றும் y=cosx.

y=f(x) சார்பு என்று சொல்கிறார்கள் ஒற்றைப்படை, x இன் அனைத்து மதிப்புகளுக்கும் f(-x)=-f(x) என்றால். ஒற்றைப்படை செயல்பாடுகளின் வரைபடங்கள் எப்போதும் தோற்றம் பற்றிய சமச்சீராக இருக்கும்.

பல செயல்பாடுகள் இரட்டை அல்லது ஒற்றைப்படை அல்ல.

கொசைன்களில் ஃபோரியர் தொடர் விரிவாக்கம்.

2π காலத்துடன் கூடிய சம காலச் சார்பின் ஃபோரியர் தொடர் f(x) ஆனது கொசைன் சொற்களை மட்டுமே கொண்டுள்ளது (அதாவது சைன் சொற்கள் இல்லை) மேலும் ஒரு நிலையான சொல்லையும் உள்ளடக்கியிருக்கலாம். எனவே,

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

2π காலத்துடன் கூடிய ஒற்றைப்படை காலச் செயல்பாட்டின் ஃபோரியர் தொடர் f(x) ஆனது சைன்களுடன் சொற்களை மட்டுமே கொண்டுள்ளது (அதாவது, இது கொசைன்களுடன் சொற்களைக் கொண்டிருக்கவில்லை).

எனவே,

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

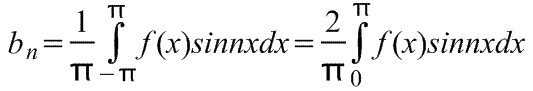
அரை சுழற்சியில் ஃபோரியர் தொடர்.

வரம்பிற்கு ஒரு செயல்பாடு வரையறுக்கப்பட்டால், 0 முதல் π வரை சொல்லுங்கள், 0 முதல் 2π வரை மட்டும் அல்ல, அது சைன்களில் அல்லது கோசைன்களில் மட்டுமே தொடரில் விரிவாக்கப்படும். இதன் விளைவாக வரும் ஃபோரியர் தொடர் அழைக்கப்படுகிறது அரை சுழற்சியில் ஃபோரியருக்கு அருகில்.

நீங்கள் சிதைவு பெற விரும்பினால் கொசைன்கள் மூலம் அரை-சுழற்சி ஃபோரியர் 0 முதல் π வரையிலான வரம்பில் f(x) செயல்பாடுகள், பின்னர் சீரான காலச் செயல்பாட்டை உருவாக்குவது அவசியம். படத்தில். x=0 முதல் x=π வரையிலான இடைவெளியில் கட்டப்பட்ட f(x)=x சார்பு கீழே உள்ளது. சமச் செயல்பாடு f(x) அச்சில் சமச்சீராக இருப்பதால், படத்தில் காட்டப்பட்டுள்ளபடி AB கோடு வரைகிறோம். கீழே. நாம் கருதப்படும் இடைவெளிக்கு வெளியே 2π காலத்துடன் விளைந்த முக்கோண வடிவம் குறிப்பிட்ட கால இடைவெளியில் இருப்பதாகக் கருதினால், இறுதி வரைபடம் இப்படி இருக்கும்: படத்தில். கீழே. கோசைன்களில் ஃபோரியர் விரிவாக்கத்தை நாம் பெற வேண்டும் என்பதால், முன்பு போலவே, ஃபோரியர் குணகங்களை a o மற்றும் a n கணக்கிடுகிறோம்

நீங்கள் பெற வேண்டும் என்றால் ஃபோரியர் அரை சுழற்சி சைன் விரிவாக்கம் 0 முதல் π வரையிலான வரம்பில் f(x) செயல்பாடுகள், பின்னர் ஒற்றைப்படை காலச் செயல்பாட்டை உருவாக்குவது அவசியம். படத்தில். x=0 முதல் x=π வரையிலான இடைவெளியில் கட்டப்பட்ட f(x)=x சார்பு கீழே உள்ளது. ஏனெனில் ஒற்றைப்படை செயல்பாடுதோற்றம் பற்றிய சமச்சீர், படத்தில் காட்டப்பட்டுள்ளபடி வரி சிடியை உருவாக்குகிறோம். கருதப்பட்ட இடைவெளிக்கு வெளியே 2π காலத்துடன் விளைந்த மரத்தூள் சமிக்ஞை குறிப்பிட்ட கால இடைவெளியில் இருக்கும் என்று நாம் கருதினால், இறுதி வரைபடம் படம் 1 இல் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டுள்ளது. சைன்களின் அடிப்படையில் அரை சுழற்சியின் ஃபோரியர் விரிவாக்கத்தை நாம் பெற வேண்டும் என்பதால், முன்பு போலவே, ஃபோரியர் குணகத்தைக் கணக்கிடுகிறோம். பி

தன்னிச்சையான இடைவெளிக்கான ஃபோரியர் தொடர்.

காலகட்டம் L உடன் ஒரு காலச் செயல்பாட்டின் விரிவாக்கம்.

x ஆனது L ஆல் அதிகரிக்கும் போது f(x) கால சார்பு மீண்டும் நிகழ்கிறது, அதாவது. f(x+L)=f(x). 2π காலப்பகுதியுடன் முன்னர் கருதப்பட்ட செயல்பாடுகளிலிருந்து L இன் காலகட்டத்திற்கு மாறுவது மிகவும் எளிமையானது, ஏனெனில் இது மாறியின் மாற்றத்தைப் பயன்படுத்தி செய்யப்படலாம்.

-L/2≤x≤L/2 வரம்பில் f(x) செயல்பாட்டின் ஃபோரியர் தொடரைக் கண்டறிய, புதிய மாறி u ஐ அறிமுகப்படுத்துகிறோம், இதனால் f(x) சார்பு u உடன் ஒப்பிடும்போது 2π காலத்தைக் கொண்டுள்ளது. u=2πx/L எனில், u=-πக்கு x=-L/2 மற்றும் u=πக்கு x=L/2. மேலும் f(x)=f(Lu/2π)=F(u) என்றும் விடுங்கள். ஃபோரியர் தொடர் F(u) வடிவம் கொண்டது

(ஒருங்கிணைப்பு வரம்புகள் நீளம் L இன் எந்த இடைவெளியிலும் மாற்றப்படலாம், எடுத்துக்காட்டாக, 0 முதல் L வரை)

L≠2π இடைவெளியில் குறிப்பிடப்பட்ட செயல்பாடுகளுக்கான அரை-சுழற்சியில் ஃபோரியர் தொடர்.

மாற்று u=πх/Lக்கு, x=0 இலிருந்து x=L வரையிலான இடைவெளி u=0 இலிருந்து u=π வரையிலான இடைவெளிக்கு ஒத்திருக்கும். இதன் விளைவாக, செயல்பாடானது கோசைன்களில் அல்லது சைன்களில் மட்டுமே ஒரு தொடராக விரிவாக்கப்படலாம், அதாவது. வி அரை சுழற்சியில் ஃபோரியர் தொடர்.

0 முதல் L வரையிலான வரம்பில் உள்ள கொசைன் விரிவாக்கம் வடிவம் கொண்டது

காலம் 2p உடன் கூடிய சீரான காலச் செயல்பாட்டின் ஃபோரியர் தொடர் f(x) கோசைன்களுடன் கூடிய சொற்களை மட்டுமே கொண்டுள்ளது (அதாவது, சைன்களுடன் சொற்களைக் கொண்டிருக்கவில்லை) மேலும் ஒரு நிலையான சொல்லையும் உள்ளடக்கியிருக்கலாம். எனவே,

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

சைன்களில் ஃபோரியர் தொடர் விரிவாக்கம்

ஒற்றைப்படை காலச் சார்பின் ஃபோரியர் தொடர் 2p உடன் கூடிய f (x) ஆனது சைன்களுடன் சொற்களை மட்டுமே கொண்டுள்ளது (அதாவது, இது கொசைன்களுடன் சொற்களைக் கொண்டிருக்கவில்லை).

எனவே,

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

அரை சுழற்சியில் ஃபோரியர் தொடர்

வரம்பிற்கு ஒரு செயல்பாடு வரையறுக்கப்பட்டால், 0 முதல் p வரை சொல்லுங்கள், 0 முதல் 2p வரை மட்டும் அல்ல, அது சைன்களில் மட்டும் அல்லது கோசைன்களில் மட்டும் தொடராக விரிவாக்கப்படும். இதன் விளைவாக வரும் ஃபோரியர் தொடர் அழைக்கப்படுகிறது அருகில் ஃபோரியர் அன்று அரை சுழற்சி

நீங்கள் சிதைவு பெற விரும்பினால் ஃபோரியர் அன்று அரை சுழற்சி மூலம் கொசைன்கள் 0 முதல் p வரையிலான வரம்பில் f (x) செயல்பாடுகள், பிறகு சீரான காலச் செயல்பாட்டை உருவாக்குவது அவசியம். படத்தில். x = 0 இலிருந்து x = p வரையிலான இடைவெளியில் f (x) = x செயல்பாடு கீழே உள்ளது. சமச் செயல்பாடு f (x) அச்சில் சமச்சீராக இருப்பதால், படத்தில் காட்டப்பட்டுள்ளபடி AB கோடு வரைகிறோம். கீழே. கருதப்படும் இடைவெளிக்கு வெளியே 2p காலகட்டத்துடன் முக்கோண வடிவமானது குறிப்பிட்ட கால இடைவெளியில் இருக்கும் என்று நாம் கருதினால், இறுதி வரைபடம் இப்படி இருக்கும்: படத்தில். கீழே. கோசைன்களில் ஃபோரியர் விரிவாக்கத்தை நாம் பெற வேண்டும் என்பதால், முன்பு போலவே, ஃபோரியர் குணகங்களை a o மற்றும் a n கணக்கிடுகிறோம்

நீங்கள் பெற வேண்டும் என்றால் சிதைவு ஃபோரியர் அன்று அரை சுழற்சி மூலம் சைனஸ்கள் 0 முதல் p வரையிலான வரம்பில் f (x) செயல்பாடுகள், பின்னர் ஒற்றைப்படை காலச் செயல்பாட்டை உருவாக்குவது அவசியம். படத்தில். x=0 இலிருந்து x=p வரையிலான இடைவெளியில் கட்டப்பட்ட f (x) =x செயல்பாடு கீழே உள்ளது. ஒற்றைப்படை செயல்பாடு தோற்றத்தில் சமச்சீராக இருப்பதால், படத்தில் காட்டப்பட்டுள்ளபடி, வரி சிடியை உருவாக்குகிறோம்.

கருதப்பட்ட இடைவெளிக்கு வெளியே 2p கால இடைவெளியில் விளைந்த மரத்தூள் சிக்னல் கால இடைவெளியில் இருக்கும் என்று நாம் கருதினால், இறுதி வரைபடம் படம் 1 இல் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டுள்ளது. சைன்களின் அடிப்படையில் அரை சுழற்சியின் ஃபோரியர் விரிவாக்கத்தை நாம் பெற வேண்டும் என்பதால், முன்பு போலவே, ஃபோரியர் குணகத்தைக் கணக்கிடுகிறோம். பி

செயல்பாடுகள், அவற்றை கூறுகளாக சிதைப்பது. மாற்று நீரோட்டங்கள் மற்றும் மின்னழுத்தங்கள், இடப்பெயர்வுகள், கிராங்க் பொறிமுறைகளின் வேகம் மற்றும் முடுக்கம் மற்றும் ஒலி அலைகள் ஆகியவை பொறியியல் கணக்கீடுகளில் காலமுறை செயல்பாடுகளைப் பயன்படுத்துவதற்கான பொதுவான நடைமுறை எடுத்துக்காட்டுகள்.

ஃபோரியர் தொடர் விரிவாக்கமானது -π ≤x≤ π இடைவேளையில் நடைமுறை முக்கியத்துவம் வாய்ந்த அனைத்து செயல்பாடுகளும் ஒன்றிணைந்த முக்கோணவியல் தொடரின் வடிவத்தில் வெளிப்படுத்தப்படலாம் என்ற அனுமானத்தின் அடிப்படையில் அமைந்துள்ளது. ஒன்றிணைகிறது):

sinx மற்றும் cosx கூட்டுத்தொகை மூலம் நிலையான (=சாதாரண) குறியீடு

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

இதில் a o, a 1,a 2,...,b 1,b 2,.. உண்மையான மாறிலிகள், அதாவது.

எங்கே, -π முதல் π வரையிலான வரம்பிற்கு, ஃபோரியர் தொடரின் குணகங்கள் சூத்திரங்களைப் பயன்படுத்தி கணக்கிடப்படுகின்றன:

குணகங்கள் a o , a n மற்றும் b n என்று அழைக்கப்படுகின்றன ஃபோரியர் குணகங்கள், மற்றும் அவை கண்டுபிடிக்கப்பட்டால், தொடர் (1) அழைக்கப்படுகிறது ஃபோரியருக்கு அடுத்து, f(x) சார்புடன் தொடர்புடையது. தொடர் (1), சொல் (a 1 cosx+b 1 sinx) முதல் அல்லது அடிப்படை இசைவு,

தொடரை எழுத மற்றொரு வழி acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

காலம் 2π உடன் காலமுறை அல்லாத செயல்பாடுகளின் ஃபோரியர் தொடர்.

ஃபோரியர் தொடரில் காலமுறை அல்லாத செயல்பாடுகளை விரிவுபடுத்துதல்.

சம மற்றும் ஒற்றைப்படை செயல்பாடுகள்.

பல செயல்பாடுகள் இரட்டை அல்லது ஒற்றைப்படை அல்ல.

கொசைன்களில் ஃபோரியர் தொடர் விரிவாக்கம்.

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

எனவே,

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

அரை சுழற்சியில் ஃபோரியர் தொடர்.

0 முதல் π வரையிலான வரம்பில் f(x) செயல்பாடுகளைப் பெற விரும்பினால், நீங்கள் ஒற்றைப்படை காலச் செயல்பாட்டை உருவாக்க வேண்டும். படத்தில். x=0 முதல் x=π வரையிலான இடைவெளியில் கட்டப்பட்ட f(x)=x சார்பு கீழே உள்ளது. ஒற்றைப்படை செயல்பாடு தோற்றத்தில் சமச்சீராக இருப்பதால், படத்தில் காட்டப்பட்டுள்ளபடி, வரி சிடியை உருவாக்குகிறோம். கருதப்பட்ட இடைவெளிக்கு வெளியே 2π காலத்துடன் விளைந்த மரத்தூள் சமிக்ஞை குறிப்பிட்ட கால இடைவெளியில் இருக்கும் என்று நாம் கருதினால், இறுதி வரைபடம் படம் 1 இல் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டுள்ளது. சைன்களின் அடிப்படையில் அரை சுழற்சியின் ஃபோரியர் விரிவாக்கத்தை நாம் பெற வேண்டும் என்பதால், முன்பு போலவே, ஃபோரியர் குணகத்தைக் கணக்கிடுகிறோம். பி

தன்னிச்சையான இடைவெளிக்கான ஃபோரியர் தொடர்.

காலகட்டம் L உடன் ஒரு காலச் செயல்பாட்டின் விரிவாக்கம்.

ஃபோரியர் தொடரின் குணகங்கள் எங்கே,

இருப்பினும், பெரும்பாலும் மேலே உள்ள சூத்திரம் x ஐச் சார்ந்திருக்கும். u=2πx/L என்பதால், இதன் பொருள் du=(2π/L)dx, மற்றும் ஒருங்கிணைப்பின் வரம்புகள் -L/2 இலிருந்து L/2 க்கு பதிலாக - π முதல் π வரை இருக்கும். இதன் விளைவாக, x ஐ சார்ந்திருப்பதற்கான ஃபோரியர் தொடர் வடிவம் கொண்டது

-எல்/2 முதல் எல்/2 வரையிலான வரம்பில் ஃபோரியர் தொடரின் குணகங்கள் உள்ளன,

L≠2π இடைவெளியில் குறிப்பிடப்பட்ட செயல்பாடுகளுக்கான அரை-சுழற்சியில் ஃபோரியர் தொடர்.

0 முதல் L வரையிலான வரம்பில் உள்ள கொசைன் விரிவாக்கம் வடிவம் கொண்டது

டிரான்ஸ்கிரிப்ட்

RF நோவோசிபிர்ஸ்க் மாநில பல்கலைக்கழகத்தின் இயற்பியல் பீடத்தின் 1 கல்வி மற்றும் அறிவியல் அமைச்சகம் ஆர்.

2 UDC BBK V161 B44 B44 Belkheeva R.K ஃபோரியர் தொடர் உதாரணங்கள் மற்றும் சிக்கல்கள்: பாடநூல் / நோவோசிபிர்ஸ்க். மாநில பல்கலைக்கழகம் நோவோசிபிர்ஸ்க், எஸ். ஐஎஸ்பிஎன் பி பாடநூல்ஃபோரியர் தொடர் பற்றிய அடிப்படை தகவல்கள் வழங்கப்படுகின்றன, ஆய்வு செய்யப்பட்ட ஒவ்வொரு தலைப்புக்கும் எடுத்துக்காட்டுகள் கொடுக்கப்பட்டுள்ளன. ஒரு சரத்தின் குறுக்கு அதிர்வுகளின் சிக்கலைத் தீர்க்க ஃபோரியர் முறையைப் பயன்படுத்துவதற்கான எடுத்துக்காட்டு விரிவாக பகுப்பாய்வு செய்யப்படுகிறது. விளக்கப் பொருள் வழங்கப்படுகிறது. அதற்கான பணிகள் உள்ளன சுதந்திரமான முடிவு. NSU இன் இயற்பியல் பீடத்தின் மாணவர்கள் மற்றும் ஆசிரியர்களுக்காக வடிவமைக்கப்பட்டுள்ளது. NSU இன் இயற்பியல் பீடத்தின் வழிமுறை ஆணையத்தின் முடிவால் வெளியிடப்பட்டது. மதிப்பாய்வாளர்: டாக்டர் இயற்பியல்-கணிதம். அறிவியல் V. A. Aleksandrov பல ஆண்டுகளாக NRU-NSU மேம்பாட்டுத் திட்டத்தை செயல்படுத்துவதன் ஒரு பகுதியாக கையேடு தயாரிக்கப்பட்டது. நோவோசிபிர்ஸ்கில் இருந்து ISBN மாநில பல்கலைக்கழகம், 211 சி பெல்கீவா ஆர்.கே., 211

3 1. ஒரு ஃபோரியர் தொடர் வரையறையாக 2π-காலச் செயல்பாட்டின் விரிவாக்கம். F(x) செயல்பாட்டின் ஃபோரியர் தொடர் a 2 + (a n cosnx + b n sin nx), (1) இதில் குணகங்கள் a n, b n சூத்திரங்களைப் பயன்படுத்தி கணக்கிடப்படுகின்றன: a n = 1 π b n = 1 π f (x) cosnxdx, n = , 1,..., (2) f(x) sin nxdx, n = 1, 2,.... (3) சூத்திரங்கள் (2) (3) யூலர் ஃபோரியர் சூத்திரங்கள் எனப்படும். F(x) சார்பு ஃபோரியர் தொடர் (1) உடன் ஒத்துப்போகிறது என்பது f(x) a 2 + (a n cosnx + b n sin nx) (4) என்ற சூத்திரத்தின் வடிவத்தில் எழுதப்பட்டு வலது பக்கம் என்று கூறுகிறோம். ஃபார்முலா (4) என்பது ஒரு முறையான தொடர் ஃபோரியர் செயல்பாடு f(x) ஆகும். வேறு வார்த்தைகளில் கூறுவதானால், சூத்திரம் (4) என்பது ஒரு n, b n குணகங்கள் சூத்திரங்களைப் பயன்படுத்தி கண்டுபிடிக்கப்பட்டது என்று மட்டுமே பொருள் (2), (3). 3

4 வரையறை. [, π] இடைவெளியில் வரையறுக்கப்பட்ட புள்ளிகள் = x இருந்தால், 2π-கால சார்பு f(x) துண்டு துண்டாக மென்மையானது என அழைக்கப்படுகிறது.< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 படம். 1. f(x) செயல்பாட்டின் வரைபடம் a = 1 π f(x) dx = 1 π x 2 2 π = π, a n = 1 π f(x) cosnxdx = 2 π = 2 () x ஃபோரியர் குணகங்களைக் கணக்கிடவும் sin nx cos nx + π n n 2 = 2 π (1) n 1 n 2 = b n = 1 π π = 2 π f(x) cosnxdx = cos nx cos n 2 = 4 πn2, n ஒற்றைப்படை, n இரட்டைக்கு f(x ) sin nxdx =, ஏனெனில் f(x) செயல்பாடு சமமாக உள்ளது. f(x) செயல்பாட்டிற்கான முறையான ஃபோரியர் தொடரை எழுதுவோம்: f(x) π 2 4 π k= 5 cos (2k + 1)x (2k + 1) 2.

6 f(x) செயல்பாடு துண்டு துண்டாக உள்ளதா என்பதைக் கண்டுபிடிப்போம். இது தொடர்ச்சியாக இருப்பதால், x = ±π இடைவெளியின் இறுதிப் புள்ளிகளில் வரம்புகள் (6) மற்றும் இடைவேளை புள்ளியில் x = : மற்றும் f(π h) f(π) π h π lim = lim h + h h + h = 1, f(+ h) f(+) + h () lim = lim h + h h + h f(+ h) f(+) + h lim = lim = 1, h + h h + h = 1 , f(h) f () h () lim = lim = 1. h + h h + h வரம்புகள் உள்ளன மற்றும் வரையறுக்கப்பட்டுள்ளன, எனவே செயல்பாடு துண்டு துண்டாக மென்மையானது. பாயிண்ட் வைஸ் கன்வர்ஜென்ஸ் தேற்றம் மூலம், அதன் ஃபோரியர் தொடர் ஒவ்வொரு புள்ளியிலும் f(x) என்ற எண்ணுடன் ஒன்றிணைகிறது, அதாவது f(x) = π 2 4 π k= cos (2k + 1) + x (2k + 1) 2 = = π 2 4 (cosx + 19 π cos 3x) cos 5x (7) படத்தில். 2, 3 ஃபோரியர் தொடர் S n (x) இன் பகுதித் தொகைகளின் தோராயமான தன்மையைக் காட்டுகிறது, இங்கு S n (x) = a n 2 + (a k coskx + b k sin kx), k=1 செயல்பாட்டிற்கு f(x) ) இடைவெளியில் [, π] . 6

7 படம். 2. F(x) செயல்பாட்டின் வரைபடம் S (x) = a 2 மற்றும் S 1(x) = a 2 + a 1 cos x படம். 3. f(x) செயல்பாட்டின் வரைபடம் அதன் மீது பகுதித் தொகையின் வரைபடம் S 99 (x) = a 2 + a 1 cos x + + a 99 cos 99x 7

8 x = (7) ஐ மாற்றினால் நாம் பெறுவது: = π 2 4 π k= 1 (2k + 1) 2, எங்கிருந்து நாம் எண் தொடரின் கூட்டுத்தொகையைக் காண்கிறோம்: = π2 8. இந்தத் தொடரின் கூட்டுத்தொகையை அறிந்தால், அது பின்வரும் தொகையை கண்டுபிடிப்பது எளிது: S = ( ) S = () = π S, எனவே S = π2 6, அதாவது 1 n = π இந்த புகழ்பெற்ற தொடரின் கூட்டுத்தொகை முதலில் லியோன்ஹார்ட் யூலர் என்பவரால் கண்டுபிடிக்கப்பட்டது. இது பெரும்பாலும் கணித பகுப்பாய்வு மற்றும் அதன் பயன்பாடுகளில் காணப்படுகிறது. எடுத்துக்காட்டு 2. ஒரு வரைபடத்தை வரைந்து, xக்கான ஃபார்முலா f(x) = x கொடுக்கப்பட்ட செயல்பாட்டின் ஃபோரியர் தொடரைக் கண்டுபிடிப்போம்.< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 படம். 4. f(x) செயல்பாட்டின் வரைபடம் f(x) சார்பு இடைவேளையில் (, π) தொடர்ச்சியாக வேறுபடுகிறது. புள்ளிகளில் x = ±π, இது வரையறுக்கப்பட்ட வரம்புகளைக் கொண்டுள்ளது (5): f() =, f(π) = π. கூடுதலாக, வரையறுக்கப்பட்ட வரம்புகள் உள்ளன (6): f(+ h) f(+) lim = 1 மற்றும் h + h f(π h) f(π +) lim = 1. h + h எனவே, f(x) piecewise மென்மையான செயல்பாடு. f(x) சார்பு ஒற்றைப்படை என்பதால், a n =. பாகங்கள் மூலம் ஒருங்கிணைத்து b n குணகங்களைக் காண்கிறோம்: b n = 1 π f(x) sin πnxdx= 1 [ x cosnx π πn + 1 n = 1 πn [(1)n π + (1) n π] = 2(1 )n+ 1. n 2(1) n+1 f(x) sin nx செயல்பாட்டின் முறையான ஃபோரியர் தொடரை உருவாக்குவோம். n 9 cosnxdx ] =

10 துண்டு துண்டாக மென்மையான 2π-காலச் செயல்பாட்டின் புள்ளியாக ஒன்றிணைந்த தேற்றத்தின்படி, f(x) செயல்பாட்டின் ஃபோரியர் தொடர் கூட்டுத்தொகைக்கு இணைகிறது: 2(1) n+1 sin nx = n f(x) = x, π என்றால்< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 படம். 6. F(x) செயல்பாட்டின் வரைபடம் S 2 (x) என்ற பகுதியின் வரைபடத்துடன் படம். 7. F(x) செயல்பாட்டின் வரைபடம் S 3 (x) 11 என்ற பகுதித் தொகையின் வரைபடம் அதன் மீது மிகைப்படுத்தப்பட்டுள்ளது

12 படம். 8. F(x) செயல்பாட்டின் வரைபடம் S 99 (x) இன் ஒரு வரைபடத்துடன் இரண்டு எண் தொடர்களின் கூட்டுத்தொகையைக் கண்டறிய அதன் விளைவாக வரும் ஃபோரியர் தொடரைப் பயன்படுத்துகிறோம். x = π/2 ஐ (8) இல் வைப்போம். பின்னர் 2 () +... = π 2, அல்லது = n= (1) n 2n + 1 = π 4. பிரபலமான லீப்னிஸ் தொடரின் கூட்டுத்தொகையை எளிதாகக் கண்டுபிடித்தோம். (8) இல் x = π/3 ஐ வைத்து () +... = π 2 3, அல்லது (1+ 1) () (k) 3π +...= 3k

13 எடுத்துக்காட்டு 3. ஒரு வரைபடத்தை வரைவோம், f(x) = sin x செயல்பாட்டின் ஃபோரியர் தொடரைக் கண்டுபிடி, அது 2π காலத்தைக் கொண்டிருப்பதாகக் கருதி, 1 எண் தொடரின் கூட்டுத்தொகை 4n 2 1. தீர்வு. f(x) செயல்பாட்டின் வரைபடம் படத்தில் காட்டப்பட்டுள்ளது. 9. வெளிப்படையாக, f(x) = sin x என்பது π காலத்துடன் ஒரு தொடர்ச்சியான சீரான செயல்பாடு ஆகும். ஆனால் 2π என்பது f(x) செயல்பாட்டின் காலம் ஆகும். அரிசி. 9. f(x) செயல்பாட்டின் வரைபடம் ஃபோரியர் குணகங்களைக் கணக்கிடுவோம். அனைத்து b n = செயல்பாடு சமமாக இருப்பதால். முக்கோணவியல் சூத்திரங்களைப் பயன்படுத்தி, n 1க்கான nஐக் கணக்கிடுகிறோம்: a n = 1 π = 1 π sin x cosnxdx = 2 π sin x cosnxdx = (sin(1 + n)x sin(1 n)x) dx = = 1 () π cos( 1 + n)x cos(1 n)x + = 2 () 1 + (1) n = π 1 + n 1 n π 1 n 2 ( 4 1 என்றால் n = 2k, = π n 2 1 என்றால் n = 2k

14 இந்தக் கணக்கீடு, குணகம் a 1ஐக் கண்டறிய அனுமதிக்காது, ஏனெனில் n = 1 இல் வகுத்தல் பூஜ்ஜியத்திற்குச் செல்கிறது. எனவே, குணகம் a 1 ஐ நேரடியாகக் கணக்கிடுகிறோம்: a 1 = 1 π sin x cosxdx =. f(x) ஆனது (,) மற்றும் (, π) மற்றும் kπ புள்ளிகளில் (k ஒரு முழு எண்) தொடர்ந்து வேறுபடுவதால், வரையறுக்கப்பட்ட வரம்புகள் (5) மற்றும் (6) உள்ளன, பின்னர் செயல்பாட்டின் ஃபோரியர் தொடர் ஒன்றிணைகிறது. ஒவ்வொரு புள்ளியிலும் அதற்கு: = 2 π 4 π sinx = 2 π 4 π cos 2nx 4n 2 1 = (1 1 cos 2x cos 4x + 1) cos 6x f(x) செயல்பாட்டின் தோராயமான தன்மையை படம் காட்டுகிறது ஃபோரியர் தொடரின் பகுதித் தொகைகள் மூலம்.. (9) படம். 1. F(x) செயல்பாட்டின் வரைபடம் S (x) 14 என்ற பகுதித் தொகையின் வரைபடம் அதன் மீது மிகைப்படுத்தப்பட்டுள்ளது

15 படம். 11. F(x) செயல்பாட்டின் வரைபடம் S 1 (x) என்ற பகுதித் தொகையின் வரைபடம். 12. f(x) செயல்பாட்டின் வரைபடம் S 2 (x) என்ற பகுதித் தொகையின் வரைபடம். 13. F(x) செயல்பாட்டின் வரைபடம், அதன் மீது பகுதித் தொகையின் வரைபடம் S 99 (x) 15

16 1 எண் தொடரின் கூட்டுத்தொகையைக் கணக்கிடவும். இதைச் செய்ய, (9) x = இல் 4n 2 1 ஐ வைக்கவும். பின்னர் cosnx = 1 அனைத்து n = 1, 2,... எனவே, 2 π 4 π 1 4n 2 1 =. 1 4n 2 1 = = 1 2. உதாரணம் 4. ஒரு துண்டு துண்டாக மென்மையான தொடர்ச்சியான செயல்பாடு f(x) அனைத்து x க்கும் f(x π) = f(x) நிபந்தனையை பூர்த்தி செய்தால் (அதாவது π-காலம்) , பின்னர் a 2n 1 = b 2n 1 = அனைத்து n 1 க்கும், மற்றும் நேர்மாறாகவும், 2n 1 = b 2n 1 = அனைத்து n 1 க்கும், f(x) என்பது π-காலம் ஆகும். தீர்வு. f(x) சார்பு π-காலமாக இருக்கட்டும். அதன் ஃபோரியர் குணகங்கள் a 2n 1 மற்றும் b 2n 1: = 1 π (a 2n 1 = 1 π f(x) cos(2n 1)xdx + f(x) cos(2n 1)xdx =) f(x) cos (2n 1)xdx. முதல் ஒருங்கிணைப்பில் x = t π: f(x) cos(2n 1)xdx = f(t π) cos(2n 1)(t + π) dt என்ற மாறியை மாற்றுவோம். 16

17 cos(2n 1)(t + π) = cos(2n 1)t மற்றும் f(t π) = f(t) என்ற உண்மையைப் பயன்படுத்தி, நாம் பெறுகிறோம்: a 2n 1 = 1 π (f(x) cos( 2n 1)x dx+) f(x) cos(2n 1)x dx =. இதேபோல் b 2n 1 = என்று நிரூபிக்கப்பட்டுள்ளது. மாறாக, a 2n 1 = b 2n 1 =. f(x) சார்பு தொடர்ச்சியாக இருப்பதால், அதன் ஃபோரியர் தொடரின் மூலம் ஒரு புள்ளியில் செயல்பாட்டின் பிரதிநிதித்துவம் குறித்த தேற்றத்தின் மூலம், நாம் F(x π) = = f(x) = (a 2n cos 2nx + b 2n பாவம் 2nx). (a2n cos 2n(x π) + b 2n sin 2n(x π)) = (a2n cos 2nx + b 2n sin 2nx) = f(x), அதாவது f(x) என்பது π-கால சார்பு. எடுத்துக்காட்டு 5. துண்டாக மென்மையான செயல்பாடு f(x) அனைத்து xக்கும் f(x) = f(x) நிபந்தனையை பூர்த்தி செய்தால், a = மற்றும் a 2n = b 2n = அனைத்து n 1க்கும், மற்றும் நேர்மாறாகவும் , a = a 2n = b 2n = என்றால், அனைத்து x க்கும் f(x π) = f(x). தீர்வு. f(x) செயல்பாடு f(x π) = f(x) நிபந்தனையை பூர்த்தி செய்யட்டும். அதன் ஃபோரியர் குணகங்களைக் கணக்கிடுவோம்: 17

18 = 1 π (a n = 1 π f(x) cos nxdx + f(x) cosnxdx =) f(x) cosnxdx. முதல் ஒருங்கிணைப்பில் x = t π என்ற மாறியை மாற்றுவோம். பிறகு f(x) cosnxdx = f(t π) cosn(t π) dt. cos n(t π) = (1) n cosnt மற்றும் f(t π) = f(t) என்ற உண்மையைப் பயன்படுத்தி, நாம் பெறுகிறோம்: a n = 1 π ((1) n) f(t) cosnt dt = என்றால் n கூட, = 2 π f(t) cos nt dt, n ஒற்றைப்படை என்றால். π இதேபோல் b 2n = என்று நிரூபிக்கப்பட்டுள்ளது. மாறாக, அனைத்து n 1க்கும் a = a 2n = b 2n = என விடுங்கள். f(x) சார்பு தொடர்ச்சியாக இருப்பதால், அதன் ஃபோரியர் தொடரின் மூலம் ஒரு புள்ளியில் அதன் பிரதிநிதித்துவம் குறித்த தேற்றத்தின் மூலம், சமத்துவம் f( x) = (a 2n 1 cos (2n 1)x + b 2n 1 sin (2n 1)x). 18

19 பிறகு = f(x π) = = = f(x). உதாரணம் 6. F(x) சார்பு [, π/2] இன் இடைவேளையில் [, π] க்கு ஒருங்கிணைக்கக்கூடிய செயல்பாட்டை எவ்வாறு நீட்டிப்பது என்பதை ஆராய்வோம், அதன் ஃபோரியர் தொடரின் வடிவம்: a 2n 1 cos(2n 1) x (1) தீர்வு. செயல் வரைபடம் படத்தில் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டிருக்கட்டும். 14. தொடரில் (1) a = a 2n = b 2n = அனைத்திற்கும் n, பின்னர் உதாரணம் 5 இலிருந்து f(x) சார்பு f(x π) = f(x) அனைத்து xக்கும் சமமாக இருக்க வேண்டும். . இந்த அவதானிப்பு f(x) செயல்பாட்டை இடைவெளிக்கு [, /2] நீட்டிக்க ஒரு வழியை வழங்குகிறது: f(x) = f(x+π), படம். 15. தொடர் (1) இல் கொசைன்கள் மட்டுமே உள்ளன என்பதிலிருந்து, நீட்டிக்கப்பட்ட செயல்பாடு f(x) சமமாக இருக்க வேண்டும் என்று முடிவு செய்கிறோம் (அதாவது, அதன் வரைபடம் Oy அச்சில் சமச்சீராக இருக்க வேண்டும்), படம்.

20 படம். 14. செயல்பாட்டின் வரைபடம் f(x) படம். 15. f(x) செயல்பாட்டின் தொடர்ச்சியின் வரைபடம் [, /2] 2

21 எனவே, தேவையான செயல்பாடு படத்தில் காட்டப்பட்டுள்ள படிவத்தைக் கொண்டுள்ளது. 16. படம். 16. இடைவேளைக்கான f(x) செயல்பாட்டின் தொடர்ச்சியின் வரைபடம் [, π] சுருக்கமாக, செயல்பாடு பின்வருமாறு தொடர வேண்டும் என்று முடிவு செய்கிறோம்: f(x) = f(x), f(π x) = f(x), அதாவது [π/2, π] இடைவெளியில், f(x) செயல்பாட்டின் வரைபடம் புள்ளியை (π/2,) பொறுத்து மையமாக சமச்சீர் மற்றும் இடைவெளியில் [, π], அதன் வரைபடம் Oy அச்சைப் பொறுத்து சமச்சீராக உள்ளது. 21

22 எடுத்துக்காட்டுகளின் பொதுமைப்படுத்தல் 3 6 நாம் l >. இரண்டு நிபந்தனைகளைக் கருத்தில் கொள்வோம்: a) f(l x) = f(x); b) f(l + x) = f(x), x [, l/2]. உடன் வடிவியல் புள்ளிபார்வையின் அடிப்படையில், நிபந்தனை (a) என்பது f(x) செயல்பாட்டின் வரைபடம் x = l/2 என்ற செங்குத்து கோட்டுடன் சமச்சீராக உள்ளது, மேலும் நிபந்தனை (b) f(x) இன் வரைபடம் மைய சமச்சீர் abscissa அச்சில் (l/2;) புள்ளியைப் பொறுத்து. பின்னர் பின்வரும் கூற்றுகள் உண்மையாக இருக்கும்: 1) f(x) செயல்பாடு சமமாகவும், நிபந்தனை (a) திருப்திகரமாகவும் இருந்தால், b 1 = b 2 = b 3 =... =, a 1 = a 3 = a 5 = ... = ; 2) f(x) செயல்பாடு சமமாகவும், நிபந்தனை (b) திருப்தியாகவும் இருந்தால், b 1 = b 2 = b 3 =... =, a = a 2 = a 4 =... = ; 3) செயல்பாடு f(x) ஒற்றைப்படை மற்றும் நிபந்தனை (a) திருப்தி அடைந்தால், a = a 1 = a 2 =... =, b 2 = b 4 = b 6 =... = ; 4) செயல்பாடு f(x) ஒற்றைப்படை மற்றும் நிபந்தனை (b) திருப்தி அடைந்தால், a = a 1 = a 2 =... =, b 1 = b 3 = b 5 =... =. சிக்கல்கள் 1 7 சிக்கல்களில், வரைபடங்களை வரைந்து, செயல்பாடுகளுக்கான ஃபோரியர் தொடர்களைக் கண்டறியவும், (அவற்றின் கால அளவு 2π: என்றால்< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 ( 1 என்றால் /2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. இடைவெளியில் கொடுக்கப்பட்ட ஒரு செயல்பாட்டின் விரிவாக்கம் [, π], சைன்களில் மட்டும் அல்லது கோசைன்களில் மட்டும் f சார்பு [, π] இடைவெளியில் கொடுக்கப்படட்டும். இந்த இடைவெளியில் அதை ஃபோரியர் தொடராக விரிவுபடுத்த விரும்புகிறோம், முதலில் f ஐ இடைவெளியில் [, π] ஒரு தன்னிச்சையான வழியில் நீட்டிக்கிறோம், பின்னர் யூலரின் ஃபோரியர் சூத்திரங்களைப் பயன்படுத்துகிறோம். ஒரு செயல்பாட்டின் தொடர்ச்சியில் உள்ள தன்னிச்சையானது அதே செயல்பாட்டிற்கு f: [, π] R வெவ்வேறு ஃபோரியர் தொடர்களைப் பெறலாம். ஆனால் நீங்கள் இந்த தன்னிச்சையைப் பயன்படுத்தி சைன்களில் அல்லது கோசைன்களில் மட்டுமே விரிவாக்கத்தைப் பெறலாம்: முதல் வழக்கில் f ஐ ஒற்றைப்படை முறையிலும், இரண்டாவது சமமான முறையிலும் தொடர்ந்தால் போதும். தீர்வு அல்காரிதம் 1. செயல்பாட்டை ஒற்றைப்படை (இரட்டை) முறையில் (,) தொடரவும், பின்னர் அவ்வப்போது 2π காலத்துடன் முழு அச்சில் செயல்பாட்டைத் தொடரவும். 2. ஃபோரியர் குணகங்களைக் கணக்கிடுங்கள். 3. f(x) செயல்பாட்டின் ஃபோரியர் தொடரை உருவாக்கவும். 4. தொடரின் ஒருங்கிணைப்புக்கான நிபந்தனைகளை சரிபார்க்கவும். 5. இந்தத் தொடர் ஒன்றிணைக்கும் செயல்பாட்டைக் குறிக்கவும். எடுத்துக்காட்டு 7. f(x) = cosx, செயல்பாட்டை விரிவாக்குவோம்< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 படம். 17. நீட்டிக்கப்பட்ட செயல்பாட்டின் வரைபடம் f (x) செயல்பாடு துண்டு துண்டாக மென்மையானது என்பது தெளிவாகிறது. ஃபோரியர் குணகங்களைக் கணக்கிடுவோம்: a n = அனைத்து n க்கும், ஏனெனில் f (x) செயல்பாடு ஒற்றைப்படை. n 1 எனில், b n = 2 π f(x) sin πnxdx = 2 π cosx sin nxdx = = 2 π dx = = 2 π cos (n + 1) x cos (n 1) x + = π n + 1 n 1 = 1 (1) n (1)n 1 1 = π n + 1 n 1 = 1, என்றால் n = 2 k + 1, (1)n+1 (n 1) + (n + 1) = π ( n + 1)(n 1) 2 2n, n = 2k என்றால். π n 2 1 முந்தைய கணக்கீடுகளில் n = 1 ஆக இருக்கும் போது, வகுத்தல் பூஜ்ஜியத்திற்கு செல்கிறது, எனவே குணகம் b 1 ஐ நேரடியாக 25 கணக்கிடலாம்

26 இயற்கையாக: b 1 = 2 π cosx sin xdx =. f (x) செயல்பாட்டின் ஃபோரியர் தொடரை உருவாக்குவோம் : f (x) 8 π k=1 k 4k 2 1 sin 2kx. எஃப் (x) சார்பு துண்டு துண்டாக மென்மையாக இருப்பதால், புள்ளியில் குவியும் தேற்றத்தின் மூலம் f (x) செயல்பாட்டின் ஃபோரியர் தொடர் கூட்டுத்தொகைக்கு இணைகிறது: cosx என்றால் π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 படம். 18. F (x) செயல்பாட்டின் வரைபடம் S 1 (x) என்ற பகுதியின் வரைபடத்துடன் படம். 19. F(x) செயல்பாட்டின் வரைபடம் S 2 (x) 27 என்ற பகுதித் தொகையின் வரைபடம்

28 படம். 2. F (x) செயல்பாட்டின் வரைபடம் S 3 (x) இன் வரைபடத்துடன் படம். படம் 21 செயல்பாடு f (x) மற்றும் அதன் பகுதித் தொகை S 99 (x) ஆகியவற்றின் வரைபடங்களைக் காட்டுகிறது. அரிசி. 21. F (x) செயல்பாட்டின் வரைபடம் S 99 (x) 28 என்ற பகுதித் தொகையின் வரைபடம்

29 உதாரணம் 8. f(x) = e ax, a >, x [, π] செயல்பாட்டை ஃபோரியர் தொடராக கொசைன்களில் மட்டும் விரிவாக்குவோம். தீர்வு. செயல்பாட்டை சமமாக (,) (அதாவது, f(x) = f(x) சமத்துவம் அனைத்து x (, π) க்கும் வைத்திருக்கும், பின்னர் அவ்வப்போது 2π காலத்துடன் முழு எண் கோட்டிற்கும் நீட்டிப்போம். f (x) செயல்பாட்டைப் பெறுகிறோம், இதன் வரைபடம் படம் 1 இல் காட்டப்பட்டுள்ளது. 22. செயல்பாடு f (x) புள்ளிகளில் படம். 22. நீட்டிக்கப்பட்ட செயல்பாட்டின் வரைபடம் f (x) x = kπ, k என்பது ஒரு முழு எண், கின்க்ஸ் உள்ளது. ஃபோரியர் குணகங்களைக் கணக்கிடுவோம்: b n =, f (x) சமமாக இருப்பதால். பகுதிகளால் ஒருங்கிணைத்தால் நமக்கு 29 கிடைக்கும்

30 a n = 2 π a = 2 π = 2 cosnxd(e ax) = 2 πa e ax dx = 2 π a (eaπ 1), f(x) cos πnxdx = 2 π πa eax cosnx = 2 π1 πs ) + 2n πa 2 π e ax cos nxdx = + 2n e ax sin nxdx = πa sin nxde ax = = 2 π a (eaπ cos n π 1) + 2n π sin nx π a 2ex ax 2n a 2 π a (eaπ cos n π 1) n2 a a n. 2 எனவே, a n = 2a e aπ cos n π 1. π a 2 + n 2 f (x) தொடர்ச்சியாக இருப்பதால், புள்ளியில் குவியும் தேற்றத்தின்படி அதன் ஃபோரியர் தொடர் f (x) ஆக ஒன்றிணைகிறது. அதாவது எல்லா x [, π] க்கும் எங்களிடம் f(x) = 1 π a (eaπ 1)+ 2a π k=1 e aπ (1) k 1 a 2 + k 2 coskx (x π) உள்ளது. கொடுக்கப்பட்ட இடைவிடாத செயல்பாட்டிற்கு ஃபோரியர் தொடரின் பகுதித் தொகைகளின் படிப்படியான அணுகுமுறையை புள்ளிவிவரங்கள் நிரூபிக்கின்றன. 3

31 படம். 23. செயல்பாடுகளின் வரைபடங்கள் f (x) மற்றும் S (x) படம். 24. செயல்பாடுகளின் வரைபடங்கள் f (x) மற்றும் S 1 (x) படம். 25. செயல்பாடுகளின் வரைபடங்கள் f (x) மற்றும் S 2 (x) படம். 26. செயல்பாடுகளின் வரைபடங்கள் f (x) மற்றும் S 3 (x) 31

32 படம். 27. செயல்பாடுகளின் வரைபடங்கள் f (x) மற்றும் S 4 (x) படம். 28. f (x) மற்றும் S 99 (x) செயல்பாட்டின் வரைபடங்கள் 9. f (x) = cos x, x π செயல்பாட்டை ஃபோரியர் தொடராக கொசைன்களில் மட்டும் விரிவாக்குங்கள். 1. f(x) = e ax, a >, x π என்ற செயல்பாட்டை சைன்களில் மட்டும் ஃபோரியர் தொடராக விரிவாக்குங்கள். 11. f(x) = x 2, x π செயல்பாட்டை சைன்களில் மட்டும் ஃபோரியர் தொடராக விரிவாக்குங்கள். 12. f(x) = sin ax, x π செயல்பாட்டை ஃபோரியர் தொடராக கொசைன்களில் மட்டும் விரிவாக்குங்கள். 13. f(x) = x sin x, x π செயல்பாட்டை சைன்களில் மட்டும் ஃபோரியர் தொடராக விரிவாக்குங்கள். பதில்கள் 9. cosx = cosx. 1. e ax = 2 [ 1 (1) k e aπ] k sin kx. π a 2 + k2 k=1 11. x 2 2 [ π 2 (1) n 1 π n + 2 ] n 3 ((1)n 1) sin nx. 32

33 12. a முழு எண் இல்லை என்றால், sin ax = 1 cosaπ (1 + +2a cos 2nx ) + π a 2 (2n) 2 +2a 1 + cosaπ cos(2n 1)x π a 2 (2n 1) 2; a = 2m என்பது இரட்டை எண்ணாக இருந்தால், sin 2mx = 8m cos(2n 1)x π (2m) 2 (2n 1) 2; a = 2m 1 நேர்மறை ஒற்றைப்படை எண்ணாக இருந்தால், sin(2m 1)x = 2 (cos 2nx ) 1 + 2(2m 1). π (2m 1) 2 (2n) π 16 n sin x sin 2nx. 2 π (4n 2 1) 2 3. தன்னிச்சையான காலம் கொண்ட செயல்பாட்டின் ஃபோரியர் தொடர் f(x) சார்பு [l, l], l > இடைவெளியில் கொடுக்கப்பட்டுள்ளது என்று வைத்துக்கொள்வோம். x = ly, y π ஐ மாற்றியமைப்பதன் மூலம், π [, π] இடைவெளியில் வரையறுக்கப்பட்ட g(y) = f(ly/π) செயல்பாட்டைப் பெறுகிறோம். இந்தச் சார்பு g(y) ஆனது (முறையான) ஃபோரியர் தொடர் () ly f = g(y) a π 2 + (a n cosny + b n sin ny) க்கு ஒத்திருக்கிறது, இதன் குணகங்கள் யூலர் ஃபோரியர் சூத்திரங்களைப் பயன்படுத்தி காணப்படுகின்றன: a n = 1 π g(y) cosny dy = 1 π f (ly π) cos ny dy, n =, 1, 2,..., 33

34 b n = 1 π g(y) sinny dy = 1 π f () ly sin ny dy, n = 1, 2,.... π பழைய மாறிக்கு திரும்புதல், அதாவது, எழுதப்பட்ட சூத்திரங்களில் y = πx/ l, f(x) செயல்பாட்டிற்காக, சற்று மாற்றியமைக்கப்பட்ட வடிவத்தின் முக்கோணவியல் தொடரைப் பெறுகிறோம்: f(x) a 2 + a n = 1 l b n = 1 l l l l l (a n cos πnx l f(x) cos πnx l f(x) sin πnx l + b n sin πnx), (11) l dx, n =, 1, 2,..., (12) dx, n = 1, 2,.... (13) ஃபார்முலாக்கள் (11) (13) தன்னிச்சையான காலகட்டத்துடன் ஒரு செயல்பாட்டின் ஃபோரியர் தொடர் விரிவாக்கத்தை வரையறுப்பதாக கூறப்படுகிறது. எடுத்துக்காட்டு 9. இடைவெளியில் (எல், எல்) குறிப்பிடப்பட்ட ஒரு செயல்பாட்டின் ஃபோரியர் தொடரை (ஏ, என்றால் எல்) மூலம் கண்டுபிடிப்போம்.< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 a = 1 l l f(x) dx = 1 l A dx + 1 l l B dx = A + B, l l a n = 1 l l l f(x) cos πnx l dx = = 1 l = 1 l l A cos πnx l = A + B π n l b n = 1 l dx + 1 l l B cos πnx l sin πn =, n, l l A sin πnx l f(x) sin πnx l dx + 1 l l dx = B sin πnx l = B A (1 cosπn). πn f (x) செயல்பாட்டின் ஃபோரியர் தொடரை உருவாக்குவோம் : f(x) A + B π (B A என்பதால் cosπn = (1) n, பின்னர் n dx = dx = (1 cosπn) sin πnx). l n = 2k க்கு b n = b 2k =, n = 2k 1 b n = b 2k 1 = 35 2(B A) π(2k 1) ஐப் பெறுகிறோம்.

36 எனவே f(x) A + B (B A) π (sin πx + 1 3πx sin + 1 5πx sin +... l 3 l 5 l பாயிண்ட் வைஸ் கன்வர்ஜென்ஸ் தேற்றத்தின்படி, ஃபோரியர் தொடர் f(x) கூட்டுத்தொகை A, l எனில்< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 படம். 29. F (x) செயல்பாட்டின் வரைபடம் S (x) = a 2 மற்றும் S 1 (x) = b 1 sinx என்ற ஹார்மோனிக் வரைபடங்களுடன் அதன் மீது மிகைப்படுத்தப்பட்டுள்ளது. தெளிவுக்காக, S 3 (x) = b 3 sin 3πx, S l 5 (x) = b 5 sin 5πx l மற்றும் S 7 (x) = b 7 sin 7πx ஆகிய மூன்று உயர் ஹார்மோனிக்ஸ் வரைபடங்கள் செங்குத்தாக மேல்நோக்கி l 37 மாற்றப்படுகின்றன.

38 படம். 3. F(x) செயல்பாட்டின் வரைபடம் S 99 (x) என்ற பகுதித் தொகையின் வரைபடம். 31. படம் துண்டு. 3 மற்றொரு அளவில் 38

39 சிக்கல்கள் சிக்கல்களில், கொடுக்கப்பட்ட இடைவெளியில் சுட்டிக்காட்டப்பட்ட செயல்பாடுகளை ஃபோரியர் தொடராக விரிவுபடுத்தவும். 14. f(x) = x 1, (1, 1). 15. f(x) = cos π x, [ 1, 1] f(x ) = sin π x, (2 1 if 1).< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18. f(x) = 8 (1) n n sin nπx. π 1 4n (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (l 22. a) f(x) = al 4 2) 1 (4n 2)πx cos, 2n1 2 (2n l b) f(x) = 4al (1) n 1 (2n 1)πx பாவம். π 2 (2n 1) 2 l 23. a) f(x) = (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x... b) f( x) = 4 (sin π π 2 2 x 1 3 sin 3π)+ 2 2 x (sin π π 2 x cos 2π) 2 x ஃபோரியர் தொடரின் சிக்கலான வடிவம் விரிவாக்கம் f(x) = c n e inx, இதில் c n = 1 2π f (x)e inx dx, n = ±1, ±2,..., ஃபோரியர் தொடரின் சிக்கலான வடிவம் என்று அழைக்கப்படுகிறது. ஒரு செயல்பாடு உண்மையான ஃபோரியர் தொடராக விரிவாக்கப்படும் அதே நிபந்தனைகள் பூர்த்தி செய்யப்பட்டால் சிக்கலான ஃபோரியர் தொடராக விரிவடைகிறது. 4

41 எடுத்துக்காட்டு 1. ஃபோரியர் தொடரை f(x) = e ax சூத்திரத்தால் கொடுக்கப்பட்ட செயல்பாட்டின் சிக்கலான வடிவத்தில், [, π) இடைவெளியில், ஒரு உண்மையான எண்ணைக் கண்டறியவும். தீர்வு. குணகங்களைக் கணக்கிடுவோம்: = c n = 1 2π f(x)e inx dx = 1 2π e (a in)x dx = 1 ((1) n e aπ (1) n e aπ) = (1)n sh aπ. 2π(a in) π(a in) f செயல்பாட்டின் சிக்கலான ஃபோரியர் தொடர், einx இல் f(x) sinh aπ π n= (1) n a வடிவத்தைக் கொண்டுள்ளது. f(x) செயல்பாடு துண்டு துண்டாக சீராக இருப்பதை உறுதி செய்வோம்: இடைவெளியில் (, π) இது தொடர்ந்து வேறுபடுத்தக்கூடியது, மேலும் x = ±π புள்ளிகளில் வரையறுக்கப்பட்ட வரம்புகள் (5), (6) lim h + ea (+h) = e aπ, lim h + ea(π h) = e aπ, e a(+h) e a(+) lim h + h = ae aπ e a(π h) e a(π), lim h + h = ae aπ. இதன் விளைவாக, f(x) சார்பை ஃபோரியர் தொடரான sh aπ π n= (1) n a in einx ஆல் குறிப்பிடலாம், இது கூட்டுத்தொகைக்கு இணைகிறது: ( e S(x) = ax என்றால் π< x < π, ch a, если x = ±π. 41

42 எடுத்துக்காட்டு 11. f(x) = 1 a 2 1 2a cosx + a2 சூத்திரத்தால் கொடுக்கப்பட்ட செயல்பாட்டின் சிக்கலான மற்றும் உண்மையான வடிவத்தில் ஃபோரியர் தொடரைக் கண்டறியவும்.< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 வகுத்தல் q (q (q) உடன் எல்லையற்ற வடிவியல் முன்னேற்றத்தின் கூட்டுத்தொகை என்பதை நினைவில் கொள்க.< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 இப்போது ஃபோரியர் தொடரை உண்மையான வடிவத்தில் கண்டுபிடிப்போம். இதைச் செய்ய, nக்கான n மற்றும் n எண்களைக் கொண்ட விதிமுறைகளை தொகுக்கலாம்: a n e inx + a n e inx = 2a neinx + e inx c = 1, பின்னர் 2 = 2a n cos nx. f(x) = 1 a 2 1 2a cosx + a = a n cosnx. 2 இது F(x) செயல்பாட்டின் உண்மையான வடிவத்தில் ஃபோரியர் தொடர் ஆகும். எனவே, ஒரு முழுமையையும் கணக்கிடாமல், செயல்பாட்டின் ஃபோரியர் தொடரைக் கண்டோம். அதே நேரத்தில், cos nxdx 1 2a cosx + a = 2 π an 2 1 a2, a என்ற அளவுருவைப் பொறுத்து ஒரு கடினமான ஒருங்கிணைப்பைக் கணக்கிட்டோம்.< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 a(z z 1) f(x) = 2i (1 a(z z 1) + a 2) = i 2 + i (a + a 1)z 2 2 (z a)(z a 1) = = i 2 + i () a 2 z a + a 1. z a 1 வடிவியல் முன்னேற்ற சூத்திரத்தைப் பயன்படுத்தி ஒவ்வொரு எளிய பின்னங்களையும் விரிவுபடுத்துவோம்: + a z a = a 1 z 1 a = a n z z n, n = z a 1 z a = az = a n z n. n= இது சாத்தியம் ஏனெனில் az = a/z = a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, அல்லது, இன்னும் சுருக்கமாக, c n = 1 2i a n sgnn. எனவே, சிக்கலான வடிவத்தில் ஃபோரியர் தொடர் கண்டுபிடிக்கப்பட்டுள்ளது. n மற்றும் n எண்களுடன் விதிமுறைகளைக் குழுவாக்குவதன் மூலம், செயல்பாட்டின் ஃபோரியர் தொடரை உண்மையான வடிவத்தில் பெறுகிறோம்: = f(x) = + a sin x 1 2a cosx + a + 2 (1 2i an e inx 1 2i an e inx n= +) = c n e inx = a n sin nx. மீண்டும் ஒருமுறை நாம் பின்வரும் சிக்கலான ஒருங்கிணைப்பைக் கணக்கிட முடிந்தது: sin x sin nxdx 1 2a cosx + a 2 = π an 1. (16) 45

46 சிக்கல்கள் 24. (15) ஐப் பயன்படுத்தி, உண்மையான a க்கு ஒருங்கிணைந்த cos nxdx 1 2a cosx + a 2, a > பயன்படுத்தி (16), integral sin x sin nxdx ஐ உண்மையான a, a > a cosx + a2 ஐக் கணக்கிடவும் சிக்கல்கள், செயல்பாடுகளுக்கான சிக்கலான வடிவத்தில் ஃபோரியர் தொடரைக் கண்டறியவும். 26. f(x) = sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее சிக்கலான தொடர்ஃபோரியர் உறவுகள் c n = c n, n =, ±1, ±2 ஆகிய உறவுகளால் தொடர்புபடுத்தப்படுகின்றன, [, π] இடைவெளியில் வரையறுக்கப்பட்ட f செயல்பாடு சமமானது என்பதை நிரூபிக்கவும் (அதாவது, f(x) = f(x) உறவை திருப்திப்படுத்துகிறது ), அதன் சிக்கலான ஃபோரியர் தொடரின் c n குணகங்கள் c n = c n, n = ± 1, ± 2 உறவுகளால் தொடர்புடையதாக இருந்தால் மட்டுமே, [, π] இடைவெளியில் வரையறுக்கப்பட்ட f செயல்பாடு ஒற்றைப்படை என்பதை நிரூபிக்கவும் (அதாவது, திருப்தி அளிக்கிறது தொடர்பு f(x ) = f(x)), அதன் சிக்கலான ஃபோரியர் தொடரின் குணகங்கள் c n ஆனது c n = c n, n =, ±1, ±2,.... விடைகள் 1 2π 24. a n a π a n i + e 2inx, இதில் n = உடன் தொடர்புடைய சொல் தவிர்க்கப்பட்டது. π n n = a n n cosnx. 28. ஒரு n cosnx. n= 46

47 5. லியாபுனோவின் சமத்துவ தேற்றம் (லியாபுனோவின் சமத்துவம்). f: [, π] R செயல்பாடு f 2 (x) dx ஆக இருக்கட்டும்< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n = 2 π f(x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. எனவே, f(x) செயல்பாட்டிற்கான Lyapunov சமத்துவம் வடிவம் பெறுகிறது: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. ஒரு πக்கான கடைசி சமத்துவத்திலிருந்து நாம் sin 2 na n 2 = a(π a) 2 அமைத்தல் a = π 2, n = 2k 1 க்கு sin2 na = 1 ஐயும் n = 2k க்கு sin 2 na = ஐயும் பெறுகிறோம். இதன் விளைவாக, k=1 1 (2k 1) 2 = = π2 8. எடுத்துக்காட்டு 14. f(x) = x cosx, x [, π] செயல்பாட்டிற்கு Lyapunov இன் சமத்துவத்தை எழுதி, எண்ணின் கூட்டுத்தொகையைக் கண்டறிய அதைப் பயன்படுத்துவோம். தொடர் (4n 2 + 1) 2 (4n 2 1) 4. 1 π தீர்வு. நேரடி கணக்கீடுகள் கொடுக்கின்றன = π π f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π cos = 1 4 4π

49 f(x) ஒரு சமச் சார்பு என்பதால், அனைத்திற்கும் n b n =, a n = 2 π = 1 π 1 = π(n + 1) = f(x) cosnxdx = 2 π 1 cos(n + 1 )x π (n + 1) 2 x cosxcosnxdx = x (cos(n + 1)x + cos(n 1)x) dx = 1 π sin(n + 1)xdx sin(n 1)xdx = π(n 1) π π 1 + cos(n 1)x = π(n 1) 2 1 (= (1) (n+1) 1) 1 (+ (1) (n+1) 1) = π(n + 1) 2 π(n 1) 2 () = (1)(n+1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1)(n+1) 1 n k π (n 2 1) = π (4k 2 1) 2 என்றால் n = 2k, 2 என்றால் n = 2k + 1. குணகம் a 1 தனித்தனியாக கணக்கிடப்பட வேண்டும், ஏனெனில் n = 1 க்கான பொதுவான சூத்திரத்தில் பின்னத்தின் வகுத்தல் செல்கிறது. பூஜ்ஜியத்திற்கு. = 1 π a 1 = 2 π f(x) cosxdx = 2 π x(1 + cos 2x)dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.

50 எனவே, f(x) செயல்பாட்டிற்கான லியாபுனோவின் சமத்துவம் வடிவம் கொண்டது: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π, இதிலிருந்து நாம் எண் தொடரின் கூட்டுத்தொகையை (4n 2) காண்கிறோம். + 1) 2 (4n 2 1) = π π சிக்கல்கள் 32. செயல்பாட்டிற்கான லியாபுனோவ் சமத்துவத்தை எழுதவும் ( x f(x) = 2 πx, என்றால் x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по பகுத்தறிவு செயல்பாடுகள்: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. பொதுமைப்படுத்தப்பட்ட Lyapunov சமத்துவத்தின் சிக்கலான வடிவத்தைப் பெறவும். 36. லியாபுனோவ் சமத்துவத்தின் சிக்கலான வடிவம் உண்மையான மதிப்புள்ள செயல்பாடுகளுக்கு மட்டுமல்ல, சிக்கலான மதிப்புள்ள செயல்பாடுகளுக்கும் செல்லுபடியாகும் என்பதைக் காட்டுங்கள். 5

51 π (2n + 1) = π sin 2απ 2απ = 2sin2 απ α 2 π 2 பதில்கள் + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f(x)g(x) dx= c n d n, இதில் c n என்பது ஃபோரியர் குணகம் 2π செயல்பாட்டின் f(x) மற்றும் d n என்பது ஃபோரியர் குணகம் செயல்பாடுகள் g(x) ஆகும். 6. ஃபோரியர் தொடரின் வேறுபாடு f: R R என்பது தொடர்ச்சியாக வேறுபடுத்தக்கூடிய 2π-காலச் சார்பு. அதன் ஃபோரியர் தொடர் வடிவம் கொண்டது: f(x) = a 2 + (a n cos nx + b n sin nx). இந்தச் செயல்பாட்டின் வழித்தோன்றல் f (x) ஒரு தொடர்ச்சியான மற்றும் 2π-காலச் செயல்பாடாக இருக்கும், அதற்காக நாம் ஒரு முறையான ஃபோரியர் தொடரை எழுதலாம்: f (x) a 2 + (a n cos nx + b n sin nx), இங்கு a, a n , b n, n = 1 , 2,... f (x) செயல்பாட்டின் ஃபோரியர் குணகங்கள். 51

52 தேற்றம் (ஃபோரியர் தொடரின் கால-படி-கால வேறுபாட்டின் மீது). மேலே உள்ள அனுமானங்களின் கீழ், a =, a n = nb n, b n = na n, n 1 ஆகியவை செல்லுபடியாகும் எடுத்துக்காட்டு 15. துண்டாக மென்மையான செயல்பாடு f(x) இடைவெளியில் தொடர்ந்து இருக்கட்டும். நிபந்தனை f(x)dx = திருப்தி அடைந்தால், Steklov இன் சமத்துவமின்மை எனப்படும் சமத்துவமின்மை 2 dx 2 dx உள்ளது என்பதை நிரூபிப்போம், மேலும் அதில் உள்ள சமத்துவம் f(x) = வடிவத்தின் செயல்பாடுகளுக்கு மட்டுமே இருப்பதை உறுதி செய்வோம். ஒரு காஸ்க்ஸ். வேறு வார்த்தைகளில் கூறுவதானால், ஸ்டெக்லோவின் சமத்துவமின்மை, வழித்தோன்றலின் சிறிய தன்மை (சராசரி சதுரத்தில்) செயல்பாட்டின் சிறிய தன்மையை (சராசரி சதுரத்தில்) குறிக்கிறது. தீர்வு. f(x) செயல்பாட்டை சமமான முறையில் இடைவெளிக்கு [, ] நீட்டிப்போம். நீட்டிக்கப்பட்ட செயல்பாட்டை அதே சின்னமான f(x) மூலம் குறிப்போம். பின்னர் நீட்டிக்கப்பட்ட செயல்பாடு [, π] இடைவெளியில் தொடர்ச்சியாகவும் துண்டு துண்டாக மென்மையாகவும் இருக்கும். f(x) சார்பு தொடர்ச்சியாக இருப்பதால், f 2 (x) என்பது இடைவெளியிலும் 2 dx லும் தொடர்ச்சியாக இருக்கும்.< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 தொடர்ச்சியான செயல்பாடு சமமாக இருப்பதால், b n =, a = நிபந்தனையின்படி. இதன் விளைவாக, லியாபுனோவின் சமத்துவம் 1 π 2 dx = a 2 π n வடிவத்தை எடுக்கும். (17) ஃபோரியர் தொடரின் கால-படி-கால வேறுபாட்டின் மீதான தேற்றத்தின் முடிவு f (x) க்கு திருப்திகரமாக இருப்பதை உறுதி செய்வோம், அதாவது a =, a n = nb n, b n = na n, n 1. f (x) என்ற வழித்தோன்றலை x 1, x 2,..., x N என்ற இடைவெளியில் [, π] புள்ளிகளில் கின்க்ஸ் செய்யட்டும். x =, x N+1 = π ஐக் குறிப்போம். ஒருங்கிணைப்பு இடைவெளியை [, π] N +1 இடைவெளிகளாகப் பிரிப்போம் (x, x 1),..., (x N, x N+1), அவை ஒவ்வொன்றிலும் f(x) தொடர்ந்து வேறுபடும். பின்னர், ஒருங்கிணைப்பின் சேர்க்கையின் சொத்தைப் பயன்படுத்தி, பின்னர் பகுதிகளால் ஒருங்கிணைக்கப்படுவதால், நாம் பெறுகிறோம்: b n = 1 π = 1 π = 1 π f (x) sin nxdx = 1 π N f(x) sin nx j= N f (x) sin nx j= x j+1 x j x j+1 x j n n π N j= x j+1 x j x j+1 x j f (x) sin nxdx = f(x) cosnxdx = f(x) cosnxdx = = 1 π [(f(x 1) sin nx 1 f(x) sin nx) ++ (f(x 2) sinnx 2 f(x 1) sin nx 1)

54 + (f(x N+1) sin nx N+1 f(x N) sin nx N)] na n = = 1 π na n = = 1 π na n = na n. x j+1 a = 1 f (x)dx = 1 N f (x)dx = π π j= x j = 1 N x j+1 f(x) π = 1 (f(π) f()) = . x j π j= f(x) சார்பு சீரான வழியில் தொடரப்பட்டதன் காரணமாக கடைசி சமத்துவம் ஏற்படுகிறது, அதாவது f(π) = f(). இதேபோல் நாம் n = nb n ஐப் பெறுகிறோம். ஃபோரியர் தொடரின் கால-படி-கால வேறுபாட்டின் தேற்றம் ஒரு தொடர்ச்சியான துண்டு துண்டாக மென்மையான 2π-காலச் செயல்பாட்டிற்கான [, π] இடைவெளியில் அதன் வழித்தோன்றல் முதல் வகையான இடைநிறுத்தங்களுக்கு உட்பட்டது சரியானது என்பதைக் காட்டியுள்ளோம். இதன் பொருள் f (x) a 2 + (a n cosnx + b n sin nx) = (na n)sin nx, ஏனெனில் a =, a n = nb n =, b n = na n, n = 1, 2,.... 2 டிஎக்ஸ் முதல்< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 (18) இல் உள்ள தொடரின் ஒவ்வொரு சொல்லும் (17) தொடரின் தொடர்புடைய சொல்லை விட அதிகமாகவோ அல்லது சமமாகவோ இருப்பதால், பின்னர் 2 dx 2 dx. F(x) என்பது அசல் செயல்பாட்டின் ஒரு சீரான தொடர்ச்சி என்பதை நினைவுகூர்ந்தால், எங்களிடம் 2 dx 2 dx உள்ளது. ஸ்டெக்லோவின் சமத்துவம் இதைத்தான் நிரூபிக்கிறது. ஸ்டெக்லோவின் சமத்துவமின்மையில் சமத்துவம் எந்தெந்த செயல்பாடுகளுக்கு உள்ளது என்பதை இப்போது ஆராய்வோம். குறைந்தது ஒரு n 2 க்கு, குணகம் a n பூஜ்ஜியத்திலிருந்து வேறுபட்டால், 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 சிக்கல்கள் 37. துண்டாக மென்மையான செயல்பாடு f(x) இடைவெளியில் [, π] தொடர்ச்சியாக இருக்கட்டும். நிபந்தனை f() = f(π) = திருப்தி அடையும் போது, ஸ்டெக்லோவ் சமத்துவமின்மை என்றும் அழைக்கப்படும் சமத்துவமின்மை 2 dx 2 dx உள்ளது என்பதை நிரூபித்து, அதில் உள்ள சமத்துவம் f(x) வடிவத்தின் செயல்பாடுகளுக்கு மட்டுமே உள்ளது என்பதை உறுதிப்படுத்தவும். = பி பாவம் x. 38. f சார்பு [, π] இடைவெளியில் தொடர்ச்சியாக இருக்கட்டும் மற்றும் அதில் (ஒருவேளை வரையறுக்கப்பட்ட எண்ணிக்கையிலான புள்ளிகளைத் தவிர) சதுர ஒருங்கிணைக்கக்கூடிய ஒரு derivative f (x) இருக்கட்டும். f() = f(π) மற்றும் f(x) dx = ஆகிய நிபந்தனைகள் திருப்தி அடைந்தால், விர்டிங்கர் சமத்துவமின்மை எனப்படும் சமத்துவமின்மை 2 dx 2 dx உள்ளது, மேலும் அதில் சமத்துவம் f படிவத்தின் செயல்பாடுகளுக்கு மட்டுமே உள்ளது என்பதை நிரூபிக்கவும். (x ) = A cosx + B sin x. 56

57 7. ஒரு உண்மையான பொருளைப் படிக்கும் போது (இயற்கை நிகழ்வுகள், உற்பத்தி செயல்முறை, கட்டுப்பாட்டு அமைப்புகள், முதலியன) இரண்டு காரணிகள் குறிப்பிடத்தக்கதாக மாறும்: ஆய்வின் கீழ் உள்ள பொருளைப் பற்றிய திரட்டப்பட்ட அறிவின் நிலை மற்றும் கணித கருவியின் வளர்ச்சியின் அளவு. அன்று நவீன நிலை அறிவியல் ஆராய்ச்சிபின்வரும் சங்கிலி உருவாக்கப்பட்டுள்ளது: நிகழ்வு இயற்பியல் மாதிரி கணித மாதிரி. சிக்கலின் இயற்பியல் உருவாக்கம் (மாதிரி) பின்வருமாறு: செயல்முறையின் வளர்ச்சிக்கான நிலைமைகள் மற்றும் அதை பாதிக்கும் முக்கிய காரணிகள் அடையாளம் காணப்படுகின்றன. கணித சூத்திரம் (மாதிரி) என்பது இயற்பியல் உருவாக்கத்தில் தேர்ந்தெடுக்கப்பட்ட காரணிகள் மற்றும் நிபந்தனைகளை சமன்பாடுகளின் அமைப்பில் (இயற்கணிதம், வேறுபாடு, ஒருங்கிணைந்த, முதலியன) விவரிக்கிறது. ஒரு குறிப்பிட்ட செயல்பாட்டு இடத்தில், சிக்கலுக்கான தீர்வு தனித்தனியாகவும் தொடர்ச்சியாகவும் ஆரம்ப மற்றும் எல்லை நிலைமைகளைச் சார்ந்து இருந்தால், ஒரு சிக்கல் நன்கு முன்வைக்கப்பட்டதாக அழைக்கப்படுகிறது. கணித மாதிரிபரிசீலனையில் உள்ள பொருளுக்கு ஒத்ததாக இல்லை, ஆனால் ஒரு சரத்தின் இலவச சிறிய குறுக்கு அதிர்வுகளுக்கான சமன்பாட்டின் தோராயமான விளக்கமாகும். சரத்தின் முனைகள் பாதுகாப்பாக இருக்கட்டும் மற்றும் சரம் இறுக்கமாக நீட்டப்படட்டும். நீங்கள் சரத்தை அதன் சமநிலை நிலையில் இருந்து அகற்றினால் (உதாரணமாக, அதை மீண்டும் இழுக்கவும் அல்லது அடிக்கவும்), சரம் 57 ஐத் தொடங்கும்

58 தயக்கம். சரத்தின் அனைத்து புள்ளிகளும் அதன் சமநிலை நிலைக்கு (குறுக்கு அதிர்வுகள்) செங்குத்தாக நகரும் என்றும், ஒவ்வொரு தருணத்திலும் சரம் ஒரே விமானத்தில் இருக்கும் என்றும் நாம் கருதுவோம். இந்த விமானத்தில் செவ்வக ஆய xou அமைப்பை எடுத்துக் கொள்வோம். பின்னர், நேரத்தின் ஆரம்ப தருணத்தில் t = சரம் ஆக்ஸ் அச்சில் அமைந்திருந்தால், u என்பது சமநிலை நிலையில் இருந்து சரத்தின் விலகலைக் குறிக்கும், அதாவது, abscissa x உடன் சரத்தின் புள்ளியின் நிலை. நேரத்தின் தன்னிச்சையான தருணம் t என்பது u (x, t) செயல்பாட்டின் மதிப்புக்கு ஒத்திருக்கிறது. t இன் ஒவ்வொரு நிலையான மதிப்புக்கும், u(x, t) செயல்பாட்டின் வரைபடம் t நேரத்தில் அதிர்வுறும் சரத்தின் வடிவத்தைக் குறிக்கிறது (படம் 32). x இன் நிலையான மதிப்பில், u (x, t) சார்பு, Ou அச்சுக்கு இணையான நேர் கோட்டில் abscissa x உடன் ஒரு புள்ளியின் இயக்க விதியை வழங்குகிறது, u t என்பது இந்த இயக்கத்தின் வேகம் மற்றும் இரண்டாவது வழித்தோன்றல் ஆகும். 2 u t 2 முடுக்கம் ஆகும். அரிசி. 32. ஒரு சரத்தின் எல்லையற்ற பகுதிக்கு பயன்படுத்தப்படும் விசைகள் u(x, t) செயல்பாடு பூர்த்தி செய்ய வேண்டிய ஒரு சமன்பாட்டை உருவாக்குவோம். இதைச் செய்ய, இன்னும் சில எளிமையான அனுமானங்களைச் செய்வோம். சரத்தை முற்றிலும் நெகிழ்வானதாகக் கருதுவோம் - 58

59 koy, அதாவது, சரம் வளைவதை எதிர்க்காது என்று கருதுவோம்; இதன் பொருள் சரத்தில் எழும் அழுத்தங்கள் எப்போதும் அதன் உடனடி சுயவிவரத்திற்கு தொடுநிலையாக இயக்கப்படுகின்றன. சரம் மீள் மற்றும் ஹூக்கின் சட்டத்திற்கு உட்பட்டதாக கருதப்படுகிறது; இதன் பொருள் பதற்றம் விசையின் அளவு மாற்றம் சரத்தின் நீளத்தின் மாற்றத்திற்கு விகிதாசாரமாகும். சரம் ஒரே மாதிரியானது என்று வைத்துக் கொள்வோம்; அவள் என்று அர்த்தம் நேரியல் அடர்த்திρ நிலையானது. வெளிப்புற சக்திகளை நாங்கள் புறக்கணிக்கிறோம். இலவச அதிர்வுகளை நாங்கள் பரிசீலித்து வருகிறோம் என்பதே இதன் பொருள். சரத்தின் சிறிய அதிர்வுகளை மட்டுமே படிப்போம். t இல் abscissa x உடன் புள்ளியில் உள்ள abscissa அச்சுக்கும் தொடுகோடுக்கும் இடையே உள்ள கோணத்தை ϕ(x, t) ஆல் குறிப்பதாக இருந்தால், சிறிய அலைவுகளின் நிபந்தனை மதிப்பு ϕ 2 (x, t) ϕ (x, t) உடன் ஒப்பிடுகையில் புறக்கணிக்கப்படலாம், அதாவது ϕ 2. கோணம் ϕ சிறியதாக இருப்பதால், cosϕ 1, ϕ sin ϕ tan ϕ u எனவே, மதிப்பு (u x x,) 2 ஐயும் புறக்கணிக்கலாம். அதிர்வு செயல்பாட்டின் போது சரத்தின் எந்தப் பிரிவின் நீளத்திலும் ஏற்படும் மாற்றத்தை நாம் புறக்கணிக்க முடியும் என்பதை உடனடியாகப் பின்தொடர்கிறது. உண்மையில், x 2 = x 1 + x என்பது எல் = x 2 x () 2 u dx x க்கு சமமாக இருக்கும் அப்சிஸ்ஸா அச்சின் இடைவெளியில் திட்டமிடப்பட்ட M 1 M 2 சரத்தின் நீளம். x நமது அனுமானங்களின்படி, T இன் டென்ஷன் விசையின் அளவு முழு சரத்திலும் நிலையானதாக இருக்கும் என்பதைக் காட்டுவோம். இதைச் செய்ய, t நேரத்தில் M 1 M 2 (படம் 32) சரத்தின் எந்தப் பகுதியையும் எடுத்து, நிராகரிக்கப்பட்ட பிரிவுகளின் செயல்பாட்டை மாற்றுவோம் - 59

60 கோவ் டென்ஷன் விசைகளால் டி 1 மற்றும் டி 2. நிபந்தனையின்படி, சரத்தின் அனைத்துப் புள்ளிகளும் Ou அச்சுக்கு இணையாக நகரும் மற்றும் வெளிப்புற சக்திகள்இல்லை, பின்னர் ஆக்ஸ் அச்சில் உள்ள பதற்றம் சக்திகளின் கணிப்புகளின் கூட்டுத்தொகை பூஜ்ஜியத்திற்கு சமமாக இருக்க வேண்டும்: T 1 cosϕ(x 1, t) + T 2 cosϕ(x 2, t) =. எனவே, ϕ 1 = ϕ(x 1, t) மற்றும் ϕ 2 = ϕ(x 2, t) கோணங்களின் சிறிய தன்மை காரணமாக, T 1 = T 2 என்று முடிவு செய்கிறோம். பொதுவான பொருள் T 1 = T 2 மூலம் T. இப்போது Ou அச்சில் அதே சக்திகளின் F u கணிப்புகளின் கூட்டுத்தொகையைக் கணக்கிடுவோம்: F u = T sin ϕ(x 2, t) T sin ϕ(x 1, t). (2) சிறிய கோணங்களுக்கு sin ϕ(x, t) tan ϕ(x, t), மற்றும் tan ϕ(x, t) u(x, t)/ x என்பதால், சமன்பாடு (2) F u என மீண்டும் எழுதப்படலாம். T (tg ϕ(x 2, t) tan ϕ(x 1, t)) (u T x (x 2, t) u) x (x 1, t) x x T 2 u x 2(x 1, t) x . புள்ளி x 1 தன்னிச்சையாக தேர்ந்தெடுக்கப்பட்டதால், F u T 2 u x2(x, t) x. M 1 M 2 பிரிவில் செயல்படும் அனைத்து சக்திகளும் கண்டறியப்பட்ட பிறகு, நியூட்டனின் இரண்டாவது விதியைப் பயன்படுத்துகிறோம், அதன்படி நிறை மற்றும் முடுக்கம் ஆகியவற்றின் தயாரிப்பு அனைத்து செயல்படும் சக்திகளின் கூட்டுத்தொகைக்கு சமம். M 1 M 2 சரத்தின் நிறை m = ρ l ρ x க்கு சமம், மேலும் முடுக்கம் 2 u(x, t) க்கு சமம். நியூட்டனின் t 2 சமன்பாடு வடிவம் பெறுகிறது: 2 u t (x, t) x = u 2 α2 2 x2(x, t) x, இங்கு α 2 = T ρ மாறிலி நேர்மறை எண். 6

61 x ஆல் குறைத்தால், நாம் 2 u t (x, t) = u 2 α2 2 x2(x, t) ஐப் பெறுகிறோம். (21) இதன் விளைவாக, ஒரு நேரியல் ஒரே மாதிரியான இரண்டாம்-வரிசை பகுதி வேறுபாடு சமன்பாட்டைப் பெற்றோம் நிலையான குணகங்கள். இது சரம் அதிர்வு சமன்பாடு அல்லது ஒரு பரிமாணம் என்று அழைக்கப்படுகிறது அலை சமன்பாடு. சமன்பாடு (21) என்பது நியூட்டனின் விதியின் மறுசீரமைப்பு மற்றும் சரத்தின் இயக்கத்தை விவரிக்கிறது. ஆனால் சிக்கலின் இயற்பியல் உருவாக்கத்தில் சரத்தின் முனைகள் சரி செய்யப்பட்டு, ஒரு கட்டத்தில் சரத்தின் நிலை அறியப்பட வேண்டிய தேவைகள் இருந்தன. இந்த நிபந்தனைகளை பின்வருமாறு சமன்பாடுகளாக எழுதுவோம்: a) சரத்தின் முனைகள் x = மற்றும் x = l என்ற புள்ளிகளில் நிலையானதாக இருக்கும் என்று கருதுவோம், அதாவது அனைத்து t உறவுகளுக்கும் u(, t) =, u என்று வைத்துக்கொள்வோம். (எல், டி) = ; (22) b) அந்த நேரத்தில் t = சரத்தின் நிலை f(x) செயல்பாட்டின் வரைபடத்துடன் ஒத்துப்போகிறது என்று வைத்துக்கொள்வோம், அதாவது x [, l] அனைத்திற்கும் சமத்துவம் u(x,) = என்று வைத்துக்கொள்வோம். f(x); (23) c) கணத்தில் t = abscissa x உடன் உள்ள சரத்தின் புள்ளிக்கு g(x) வேகம் கொடுக்கப்பட்டுள்ளது என்று வைத்துக்கொள்வோம், அதாவது u (x,) = g(x) என்று வைத்துக்கொள்வோம். (24) டி உறவுகள் (22) எல்லை நிபந்தனைகள் என்றும், உறவுகள் (23) மற்றும் (24) என்றும் அழைக்கப்படுகின்றன. ஆரம்ப நிலைமைகள். இலவச சிறிய குறுக்குவெட்டுகளின் கணித மாதிரி 61

சரத்தின் 62 அலைவுகள், சமன்பாடு (21) ஐ எல்லை நிலைமைகள் (22) மற்றும் ஆரம்ப நிலைகள் (23) மற்றும் (24) ஃபோரியர் முறை மூலம் சரத்தின் இலவச சிறிய குறுக்கு அலைவுகளின் சமன்பாட்டின் தீர்வு ஆகியவற்றைத் தீர்ப்பது அவசியம். சமன்பாடு (21) பகுதியில் x l,< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. (25) ஐ (21) மாற்றினால், நாம் பெறுகிறோம்: X T = α 2 X T, (26) அல்லது T (t) α 2 T(t) = X (x) X(x). (27) மாறிகளின் பிரிப்பு ஏற்பட்டது என்று அவர்கள் கூறுகிறார்கள். x மற்றும் t ஒன்றையொன்று சார்ந்திருக்காததால், (27) இல் இடது பக்கம் x ஐச் சார்ந்து இல்லை, வலது பக்கம் t ஐச் சார்ந்தது இல்லை, மேலும் இந்த உறவுகளின் மொத்த மதிப்பு 62 ஆகும்.

63 ஒரு மாறிலியாக இருக்க வேண்டும், இதை நாம் λ ஆல் குறிக்கிறோம்: T (t) α 2 T(t) = X (x) X(x) = λ. இங்கிருந்து நாம் இரண்டு சாதாரணங்களைப் பெறுகிறோம் வேறுபட்ட சமன்பாடுகள்: X (x) λx(x) =, (28) T (t) α 2 λt(t) =. (29) இந்த வழக்கில், எல்லை நிபந்தனைகள் (22) X()T(t) = மற்றும் X(l)T(t) = வடிவத்தை எடுக்கும். அவை அனைத்து t, t > க்கும் திருப்தியாக இருக்க வேண்டும் என்பதால், X() = X(l) =. (3) சமன்பாட்டிற்கான தீர்வுகளைக் கண்டுபிடிப்போம் (28) திருப்திகரமான எல்லை நிலைமைகள் (3). மூன்று வழக்குகளைக் கருத்தில் கொள்வோம். வழக்கு 1: λ >. λ = β 2 ஐக் குறிப்போம். சமன்பாடு (28) X (x) β 2 X(x) = வடிவத்தை எடுக்கும். அவரது சிறப்பியல்பு சமன்பாடு k 2 β 2 = k = ±β வேர்களைக் கொண்டுள்ளது. எனவே, சமன்பாட்டின் (28) பொதுவான தீர்வு X(x) = C e βx + De βx ஆகும். நாம் C மற்றும் D ஆகிய மாறிலிகளைத் தேர்ந்தெடுக்க வேண்டும், அதனால் எல்லை நிபந்தனைகள் (3) சந்திக்கப்படும், அதாவது X() = C + D =, X(l) = C e βl + De βl =. β இலிருந்து, இந்த சமன்பாடுகளின் அமைப்பு C = D = என்ற தனித்துவமான தீர்வைக் கொண்டுள்ளது. எனவே, X(x) மற்றும் 63

64 u(x, t). எனவே, வழக்கு 1 நாங்கள் ஒரு அற்பமான தீர்வைப் பெற்றுள்ளோம், அதை நாங்கள் மேலும் கருத்தில் கொள்ள மாட்டோம். வழக்கு 2: λ =. பின்னர் சமன்பாடு (28) X (x) = வடிவத்தை எடுக்கும் மற்றும் அதன் தீர்வு வெளிப்படையாக சூத்திரத்தால் வழங்கப்படுகிறது: X(x) = C x+d. இந்த தீர்வை எல்லை நிலைகளில் (3) மாற்றினால், நாம் X() = D = மற்றும் X(l) = Cl = ஐப் பெறுகிறோம், அதாவது C = D =. எனவே, X(x) மற்றும் u(x, t), மற்றும் எங்களிடம் மீண்டும் ஒரு அற்பமான தீர்வு உள்ளது. வழக்கு 3: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 பின்வருவனவற்றில் நாம் n நேர்மறை மதிப்புகளை n = 1, 2,..., ஏனெனில் எதிர்மறை n க்கு ஒரே மாதிரியான தீர்வுகளைப் பெறுவோம் (nπ) λ n = அளவுகள் ஈஜென் மதிப்புகள் மற்றும் செயல்பாடுகள் என்று அழைக்கப்படுகின்றன. X n (x) = C n sin πnx, எல்லை நிலைகள் (3) உடன் வேறுபட்ட சமன்பாட்டின் (28) ஐஜென் செயல்பாடுகளால். இப்போது சமன்பாட்டை (29) தீர்ப்போம். அதற்கு, சிறப்பியல்பு சமன்பாடு k 2 α 2 λ = வடிவத்தைக் கொண்டுள்ளது. (32) l 2 சமன்பாட்டின் X(x) தீர்வுகள் (28) எதிர்மறையான λ க்கு சமமான λ = n2 π 2 க்கு மட்டுமே இருப்பதை நாம் மேலே கண்டறிந்ததால், துல்லியமாக அத்தகைய λ பற்றி மேலும் பரிசீலிப்போம். சமன்பாட்டின் வேர்கள் (32) k = ±iα λ, மற்றும் சமன்பாட்டிற்கான தீர்வுகள் (29) வடிவத்தைக் கொண்டுள்ளன: T n (t) = A n sin πnαt + B n cos πnαt, (33) l இங்கு A n மற்றும் B n என்பது தன்னிச்சையான மாறிலிகள். சூத்திரங்களை (31) மற்றும் (33) (33) ஐ (25) மாற்றுவதன் மூலம், எல்லை நிபந்தனைகளை (22) பூர்த்தி செய்யும் சமன்பாட்டிற்கான (21) பகுதி தீர்வுகளைக் காண்கிறோம்: (u n (x, t) = B n cos πnαt + A n sin πnαt) C n sin πnx. l l l காரணி C n ஐ அடைப்புக்குறிக்குள் செருகி, C n A n = b n மற்றும் B n C n = a n குறியீடுகளை அறிமுகப்படுத்தி, u n (X, T) வடிவத்தில் (u n (x, t) = a n cos πnαt + b n என்று எழுதுகிறோம். sin πnαt) sin πnx. (34) l l l 65

66 u n (x, t) தீர்வுகளுடன் தொடர்புடைய சரத்தின் அதிர்வுகள் சரத்தின் இயற்கையான அதிர்வுகள் எனப்படும். சமன்பாடு (21) மற்றும் எல்லை நிலைகள் (22) நேரியல் மற்றும் ஒரே மாதிரியானவை என்பதால், தீர்வுகளின் நேரியல் கலவை (34) (u(x, t) = a n cos πnαt + b n sin πnαt) sin πnx (35) l l l ஒரு தீர்வாக இருக்கும். சமன்பாட்டிற்கு (21 ), ஒரு n மற்றும் b n குணகங்களின் சிறப்புத் தேர்வுடன் எல்லை நிலைமைகளை (22) திருப்திப்படுத்துகிறது, இது தொடரின் சீரான ஒருங்கிணைப்பை உறுதி செய்கிறது. இப்போது கரைசலின் a n மற்றும் b n குணகங்களைத் தேர்ந்தெடுப்போம் (35) அது எல்லை நிலைமைகளை மட்டும் திருப்திப்படுத்துகிறது, ஆனால் ஆரம்ப நிலைகள் (23) மற்றும் (24), f(x), g(x) ஆகியவை கொடுக்கப்பட்ட செயல்பாடுகளாகும். (மற்றும் f() = f (l) = g() = g(l) =). F(x) மற்றும் g(x) செயல்பாடுகள் ஃபோரியர் தொடரின் விரிவாக்கத்தின் நிபந்தனைகளை பூர்த்தி செய்கின்றன என்று நாங்கள் கருதுகிறோம். மதிப்பு t = (35) ஐ மாற்றினால், நாம் u (x,) = a n sin πnx l = f(x) ஐப் பெறுகிறோம். t ஐப் பொறுத்து தொடர்களை (35) வேறுபடுத்தி, t = ஐ மாற்றினால், நாம் u t (x,) = πnα b n sin πnx l l = g(x) ஐப் பெறுகிறோம், மேலும் இது f(x) மற்றும் g(x) செயல்பாடுகளின் விரிவாக்கமாகும். ஃபோரியர் தொடரில். எனவே, a n = 2 l l f(x) sin πnx l dx, b n = 2 l g(x) sin πnx dx. πnα l (36) 66

67 a n மற்றும் b n குணகங்களுக்கான வெளிப்பாடுகளை தொடரில் (35) மாற்றுவதன் மூலம், நாம் சமன்பாட்டிற்கு (21) ஒரு தீர்வைப் பெறுகிறோம், இது எல்லை நிபந்தனைகள் (22) மற்றும் ஆரம்ப நிலைகள் (23) மற்றும் (24) ஆகியவற்றை பூர்த்தி செய்கிறது. இவ்வாறு, சரத்தின் இலவச சிறிய குறுக்கு அதிர்வுகளின் சிக்கலை நாங்கள் தீர்த்தோம். ஃபார்முலா (34) மூலம் வரையறுக்கப்பட்ட சரத்தின் இலவச அலைவுகளின் சிக்கலின் ஈஜென் செயல்பாடுகளின் u n (x, t) இயற்பியல் அர்த்தத்தை தெளிவுபடுத்துவோம். u n (x, t) = α n cos πnα l α n = a 2 n + b2 n, (t + δ n) sin πnx, (37) l πnα δ n = arctan b n என்ற வடிவத்தில் அதை மீண்டும் எழுதுவோம். . l a n சூத்திரத்திலிருந்து (37) சரத்தின் அனைத்துப் புள்ளிகளும் ஒரே அதிர்வெண் ω n = πnα மற்றும் கட்டம் πnα δ n உடன் இணக்கமான அலைவுகளைச் செய்கிறது என்பது தெளிவாகிறது. அதிர்வு வீச்சு சரத்தின் l l abscissa x புள்ளியைப் பொறுத்தது மற்றும் α n sin πnx க்கு சமம். அத்தகைய அலைவு மூலம், சரத்தின் அனைத்து புள்ளிகளும் ஒரே நேரத்தில் ஒரு திசையில் அல்லது இன்னொரு திசையில் அவற்றின் அதிகபட்ச விலகலை அடைகின்றன மற்றும் ஒரே நேரத்தில் சமநிலை நிலையை கடந்து செல்கின்றன. இத்தகைய ஊசலாட்டங்கள் நிற்கும் அலைகள் என்று அழைக்கப்படுகின்றன. நிற்கும் அலையானது n + 1 நிலையான புள்ளிகளைக் கொண்டிருக்கும், இது [, l] இடைவெளியில் sin πnx = சமன்பாட்டின் வேர்களால் வழங்கப்படுகிறது. நிலையான புள்ளிகள் நிற்கும் அலை முனைகள் என்று அழைக்கப்படுகின்றன. முனைகளுக்கு இடையில் நடுவில் விலகல்கள் அதிகபட்சம் அடையும் புள்ளிகள் உள்ளன; அத்தகைய புள்ளிகள் ஆன்டினோடுகள் என்று அழைக்கப்படுகின்றன. ஒவ்வொரு சரமும் கண்டிப்பாக வரையறுக்கப்பட்ட அதிர்வெண்களின் அதிர்வுகளைக் கொண்டிருக்கலாம் ω n = πnα, n = 1, 2,.... இந்த அதிர்வெண்கள் சரத்தின் இயற்கை அதிர்வெண்கள் என்று அழைக்கப்படுகின்றன. ஒரு சரம் உருவாக்கக்கூடிய மிகக் குறைந்த எல் டோன் 67 ஆல் தீர்மானிக்கப்படுகிறது

68 குறைந்த இயற்கை அதிர்வெண் ω 1 = π T மற்றும் சரத்தின் அடிப்படை தொனி என்று அழைக்கப்படுகிறது. l ρ அதிர்வெண்களுடன் தொடர்புடைய மீதமுள்ள டோன்கள் ω n, n = 2, 3,..., ஓவர்டோன்கள் அல்லது ஹார்மோனிக்ஸ் என்று அழைக்கப்படுகின்றன. தெளிவுக்காக, அடிப்படை தொனி (படம் 33), முதல் ஓவர்டோன் (படம் 34) மற்றும் இரண்டாவது ஓவர்டோன் (படம் 35) ஆகியவற்றை உருவாக்கும் சரத்தின் வழக்கமான சுயவிவரங்களை சித்தரிப்போம். அரிசி. 33. முக்கிய தொனியை உருவாக்கும் சரத்தின் சுயவிவரம் படம். 34. முதல் மேலோட்டத்தை உருவாக்கும் சரத்தின் சுயவிவரம் படம். 35. இரண்டாவது ஓவர்டோனை வெளியிடும் சரத்தின் சுயவிவரம், சரம் ஆரம்ப நிலைகளால் நிர்ணயிக்கப்பட்ட இலவச அதிர்வுகளை நிகழ்த்தினால், u(x, t) செயல்பாடு குறிப்பிடப்படுகிறது, இது சூத்திரத்தில் (35) இருந்து பார்க்க முடியும், தனிப்பட்ட ஹார்மோனிக்ஸ் . இவ்வாறு தன்னிச்சையான ஏற்ற இறக்கம் 68

69 சரங்கள் நிற்கும் அலைகளின் மேல்நிலை. இந்த வழக்கில், சரத்தின் ஒலியின் தன்மை (தொனி, ஒலி தீவிரம், டிம்ப்ரே) ஒரு அதிர்வுறும் சரம் காற்றின் அதிர்வுகளை தூண்டுகிறது சரம் மூலம் வெளிப்படும் ஒலியாக மனித காது மூலம். ஒலியின் வலிமையானது அதிர்வுகளின் ஆற்றல் அல்லது வீச்சால் வகைப்படுத்தப்படுகிறது: அதிக ஆற்றல், ஒலியின் வலிமை அதிகமாகும். ஒலியின் சுருதி அதன் அதிர்வெண் அல்லது அதிர்வு காலத்தால் தீர்மானிக்கப்படுகிறது: அதிக அதிர்வெண், அதிக ஒலி. ஓவர்டோன்களின் இருப்பு, ஹார்மோனிக்ஸ் இடையே ஆற்றல் விநியோகம், அதாவது அதிர்வுகளை தூண்டும் முறை ஆகியவற்றால் ஒலியின் ஒலி தீர்மானிக்கப்படுகிறது. ஓவர்டோன்களின் வீச்சுகள், பொதுவாக பேசும் போது, அடிப்படை தொனியின் வீச்சை விட குறைவாக இருக்கும், மேலும் ஓவர்டோன்களின் கட்டங்கள் தன்னிச்சையாக இருக்கலாம். அதிர்வுகளின் கட்டத்திற்கு நமது காது உணர்திறன் இல்லை. எடுத்துக்காட்டாக, படத்தில் உள்ள இரண்டு வளைவுகளை ஒப்பிடுக. 36, இருந்து கடன் வாங்கப்பட்டது. இது கிளாரினெட் (அ) மற்றும் பியானோ (பி) ஆகியவற்றிலிருந்து பிரித்தெடுக்கப்பட்ட அதே அடிப்படை தொனியுடன் கூடிய ஒலியின் பதிவு. எந்த ஒலியும் ஒரு எளிய சைன் அலை அல்ல. இரண்டு நிகழ்வுகளிலும் ஒலியின் அடிப்படை அதிர்வெண் ஒன்றுதான், இது ஒரே தொனியை உருவாக்குகிறது. ஆனால் வளைவுகளின் வடிவங்கள் வேறுபட்டவை, ஏனெனில் வெவ்வேறு மேலோட்டங்கள் முக்கிய தொனியில் மிகைப்படுத்தப்படுகின்றன. ஒரு வகையில், இந்த வரைபடங்கள் டிம்பர் என்றால் என்ன என்பதைக் காட்டுகின்றன. 69

K. E. சியோல்கோவ்ஸ்கியின் பெயரிடப்பட்ட ரஷ்ய மாநில தொழில்நுட்ப பல்கலைக்கழகத்தின் உயர் நிபுணத்துவ கல்விக்கான ரஷ்ய கூட்டாட்சி மாநில பட்ஜெட் கல்வி நிறுவனம் கல்வி மற்றும் அறிவியல் அமைச்சகம்

கல்விக்கான ஃபெடரல் ஏஜென்சி ஃபெடரல் ஸ்டேட் எஜுகேஷனல் இன்ஸ்டிடியூஷன் ஆஃப் ஹையர் புரொஃபஷனல் எஜுகேஷன் சௌதர்ன் ஃபெடரல் யுனிவர்சிட்டி ஆர். எம். கவ்ரிலோவா, ஜி.எஸ். கோஸ்டெட்ஸ்காயா முறை

பெலாரஸ் குடியரசின் கல்வி அமைச்சகம் Vitebsk மாநில தொழில்நுட்ப பல்கலைக்கழக தலைப்பு. "வரிசைகள்" கோட்பாட்டு மற்றும் பயன்பாட்டு கணிதம் துறை. அசோக் உருவாக்கப்பட்டது. இ.பி. துனினா. அடிப்படை

விரிவுரை 4. ஹார்மோனிக் பகுப்பாய்வு. ஃபோரியர் தொடர் கால செயல்பாடுகள். ஹார்மோனிக் பகுப்பாய்வு அறிவியல் மற்றும் தொழில்நுட்பத்தில், அவ்வப்போது ஏற்படும் நிகழ்வுகளை, அதாவது மீண்டும் மீண்டும் நிகழும் நிகழ்வுகளை நாம் அடிக்கடி கையாள வேண்டும்.

மாஸ்கோ மாநில சிவில் ஏவியேஷன் தொழில்நுட்ப பல்கலைக்கழகம் வி.எம். லியுபிமோவ், ஈ.ஏ. ஜுகோவா, வி.ஏ. உகோவா, யு.ஏ. ஷுரினோவ் கணிதக் கையேடு, ஒழுக்கம் மற்றும் சோதனைப் பணிகளைப் படிப்பதற்காக

உள்ளடக்கங்கள் ஃபோரியர் தொடர்கள் 4 ஒரு காலச் செயல்பாட்டின் கருத்து 4 முக்கோணவியல் பல்லுறுப்புக்கோவை 6 3 ஆர்த்தோகனல் அமைப்புகளின் செயல்பாடுகள் 4 முக்கோணவியல் ஃபோரியர் தொடர் 3 5 சம மற்றும் ஒற்றைப்படை செயல்பாடுகளுக்கான ஃபோரியர் தொடர் 6 6 விரிவாக்கம்

திட்டவட்டமான ஒருங்கிணைந்த. ஒருங்கிணைந்த கூட்டுத்தொகைகள் மற்றும் திட்டவட்டமான ஒருங்கிணைப்பு y = f () என்ற சார்பு கொடுக்கப்பட்டால், [, b] என்ற இடைவெளியில் வரையறுக்கப்படுகிறது.< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

தொடர்களின் கோட்பாடு கணித பகுப்பாய்வின் மிக முக்கியமான அங்கமாகும், மேலும் இது கோட்பாட்டு மற்றும் பல நடைமுறை பயன்பாடுகளைக் கண்டறிகிறது. எண் மற்றும் செயல்பாட்டு தொடர்கள் உள்ளன.

தலைப்பு V ஃபோரியர் தொடர் விரிவுரை 6 ஒரு ஃபோரியர் தொடராக ஒரு குறிப்பிட்ட செயல்பாட்டை விரிவுபடுத்துதல் இயற்கையிலும் தொழில்நுட்பத்திலும் நிகழும் பல செயல்முறைகள் குறிப்பிட்ட கால இடைவெளியில் மீண்டும் மீண்டும் செய்யும் பண்புகளைக் கொண்டுள்ளன

6 ஃபோரியர் தொடர் 6 ஆர்த்தோகனல் அமைப்புகளின் செயல்பாடுகள் ஃபோரியர் தொடர் செயல்பாடுகளின் ஆர்த்தோகனல் அமைப்பில் ϕ () மற்றும் ψ (), வரையறுக்கப்பட்ட மற்றும் ஒருங்கிணைக்கக்கூடிய இடைவெளியில் [, ], இந்த இடைவெளியில் ஆர்த்தோகனல் எனப்படும்

இரயில்வே போக்குவரத்துக்கான ஃபெடரல் ஏஜென்சி யூரல் ஸ்டேட் டிரான்ஸ்போர்ட் யுனிவர்சிட்டி உயர் மற்றும் பயன்பாட்டு கணிதத் துறை N. P. Chuev ஹார்மோனிக் பகுப்பாய்வு முறையின் கூறுகள்

பெலாருசியன் ஸ்டேட் யுனிவர்சிட்டி ஆஃப் அப்ளைடு கணிதம் மற்றும் தகவல் அறிவியல் பீடம், உயர் கணிதவியல் துறை, பயன்பாட்டு கணிதம் மற்றும் தகவல் பீட மாணவர்களுக்கான கல்வி மற்றும் வழிமுறை கையேடு

உரைக்கான விளக்கங்கள்: அடையாளம் "சமமாக" படிக்கிறது மற்றும் அடையாளத்தின் வலது மற்றும் இடதுபுறத்தில் உள்ள சமன்பாடுகள் ஒரே மாதிரியான தீர்வுகளைக் கொண்டுள்ளன, ஐஆர் அடையாளம் உண்மையான எண்களின் தொகுப்பைக் குறிக்கிறது, உள்நுழைவு

கணித இயற்பியல் சமன்பாடுகள் 1. பகுதி வேறுபாடு சமன்பாடுகள் அறியப்படாத செயல்பாடு u (x 1, x 2,..., x n), சார்பற்ற மாறிகள் x 1, x 2,..., x n மற்றும் பகுதி தொடர்பான சமன்பாடு

1 2 உள்ளடக்கங்கள் 1 ஃபோரியர் தொடர் 5 1.1 முக்கோணவியல் ஃபோரியர் தொடர்.............. 5 1.2 சின் & காஸ் மட்டும்................... .. 7 1.3 ஃபோரியர் தொடர் சிக்கலான வடிவத்தில்........... 11 1.4 f(x) = c k?..................... .

82 4. பிரிவு 4. செயல்பாட்டு மற்றும் சக்தி தொடர் 4.2. பாடம் 3 4.2. பாடம் 3 4.2.. டெய்லர் தொடராக செயல்பாட்டின் விரிவாக்கம் 4.2 வரையறை

விரிவுரை 8 4 ஸ்டர்ம்-லியோவில் சிக்கல் சரத்தின் சிறிய குறுக்கு அதிர்வுகளை விவரிக்கும் இரண்டாம்-வரிசை பகுதி வேறுபாடு சமன்பாட்டிற்கான ஆரம்ப-எல்லை மதிப்பு சிக்கலைக் கவனியுங்கள்.

ரஷ்ய கூட்டமைப்பின் கல்வி மற்றும் அறிவியல் அமைச்சகம் ஃபெடரல் ஸ்டேட் பட்ஜெட் கல்வி நிறுவனம் உயர் தொழில்முறை கல்வி "சமரா மாநில தொழில்நுட்ப பல்கலைக்கழகம்" பயன்பாட்டு கணிதவியல் துறை

ஒரு செயல்பாட்டின் ஒருங்கிணைப்பு (ரீமான் படி) மற்றும் ஒரு திட்டவட்டமான ஒருங்கிணைப்பு சிக்கல்களைத் தீர்ப்பதற்கான எடுத்துக்காட்டுகள் 1. நிலையான செயல்பாடு f(x) = C இல் ஒருங்கிணைக்கக்கூடியது, ஏனெனில் எந்தப் பகிர்வுகளுக்கும் மற்றும் புள்ளிகளின் எந்தத் தேர்வுக்கும் ξ i ஒருங்கிணைந்ததாகும்.

உயர் கணிதப் பாடத்தில் கணக்கீடு பணிகளுக்கான முறையான வழிமுறைகள் "சாதாரண வேறுபட்ட சமன்பாடுகள் தொடர் இரட்டை ஒருங்கிணைப்புகள்" பகுதி தலைப்புத் தொடர்கள் மற்றும் மாறுபட்ட உள்ளடக்கத் தொடர்கள்

பதவிகள். எண் தொடர். அடிப்படை வரையறைகள் எண்களின் எல்லையற்ற வரிசையை கொடுக்கலாம் (எல்லையற்ற தொகை) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= எனப்படும். ஒரு எண் தொடர். எண்கள்

உள்ளடக்க அறிமுகம். அடிப்படை கருத்துக்கள்.... 4 1. வோல்டெராவின் ஒருங்கிணைந்த சமன்பாடுகள்... 5 வீட்டுப்பாட விருப்பங்கள்.... 8 2. வோல்டெராவின் ஒருங்கிணைந்த சமன்பாட்டின் தீர்வு. 10 வீட்டுப்பாட விருப்பங்கள்.... 11

விரிவுரை 3 டெய்லர் மற்றும் மெக்லாரின் தொடர் பவர் சீரிஸின் பயன்பாடு டெய்லர் மற்றும் மேக்லாரின் தொடர்களில் செயல்பாடுகளை விரிவுபடுத்துதல்.

35 7 முக்கோணவியல் ஃபோரியர் தொடர் ஃபோரியர் தொடர்கள் T காலத்துடன் கூடிய காலச் செயல்பாடுகளுக்கு.

இ.எம். தாது கணித பகுப்பாய்வு. எண் மற்றும் செயல்பாட்டுத் தொடர்கள் நோவோசிபிர்ஸ்க் 200 2 ரஷ்ய GOU VPO "நோவோசிபிர்ஸ்க் மாநில கல்வியியல் பல்கலைக்கழகம்" கல்வி மற்றும் அறிவியல் அமைச்சகம் E.M. ருடோய் கணித பகுப்பாய்வு.

நான் ஆண்டு, பணி. ரீமான் செயல்பாடு, 0, m m R(), என்றால், m, m 0, மற்றும் பின்னம் குறைக்க முடியாதது, 0, பகுத்தறிவற்றதாக இருந்தால், ஒவ்வொரு பகுத்தறிவு புள்ளியிலும் இடைவிடாது மற்றும் ஒவ்வொரு பகுத்தறிவற்ற புள்ளியிலும் தொடர்கிறது என்பதை நிரூபிக்கவும். தீர்வு.

1. மின்னியல் 1 1. மின்னியல் பாடம் 6 கார்ட்டீசியன் ஆயங்களில் மாறிகளைப் பிரித்தல் 1.1. (சிக்கல் 1.49) விமானம் z = அடர்த்தி σ (x, y) = σ பாவம் (αx) பாவம் (βy), இங்கு σ, α, β ஆகியவை மாறிலிகள் ஆகும்.

அத்தியாயம் பவர் தொடர் a a a தொடர் a a a a () ஒரு சக்தித் தொடர் என்று அழைக்கப்படுகிறது, அங்கு, a, தொடரின் குணகங்கள் எனப்படும் மாறிலிகள் சில நேரங்களில் மிகவும் பொதுவான வடிவத்தின் சக்தித் தொடர் கருதப்படுகிறது: a(a) a(a) a(a) (), எங்கே

எஸ் ஏ லாவ்ரென்சென்கோ wwwwrckoru விரிவுரை ஃபோரியர் உருமாற்றம் ஒருங்கிணைந்த உருமாற்றத்தின் கருத்து கணித இயற்பியலின் சக்திவாய்ந்த முறைகளில் ஒன்றாகும் மற்றும் இது ஒரு சக்திவாய்ந்த தீர்வாகும்.

வேறுபட்ட கால்குலஸ் கணித பகுப்பாய்வு அறிமுகம் வரிசை மற்றும் செயல்பாட்டின் வரம்பு. வரம்புகளுக்குள் நிச்சயமற்ற தன்மைகளை வெளிப்படுத்துதல். ஒரு செயல்பாட்டின் வழித்தோன்றல். வேறுபாடு விதிகள். வழித்தோன்றலின் பயன்பாடு

விரிவுரை N 7. பவர் சீரிஸ் மற்றும் டெய்லர் தொடர்கள்.. பவர் சீரிஸ்..... டெய்லர் தொடர்கள்.... 4. டெய்லர் மற்றும் மெக்லாரின் தொடர்களாக சில அடிப்படை செயல்பாடுகளை விரிவுபடுத்துதல்.... 5 4. பவர் சீரிஸின் பயன்பாடு... 7 .சக்தி

உலோகவியல் பீட உயர் கணிதத் துறை ரேங்க்ஸ் முறையான வழிமுறைகள் நோவோகுஸ்நெட்ஸ்க் 5 கல்விக்கான மத்திய நிறுவனம் உயர் தொழில்முறை கல்விக்கான மாநில கல்வி நிறுவனம்

9. ஆண்டிடெரிவேடிவ் மற்றும் காலவரையற்ற ஒருங்கிணைப்பு 9.. f() சார்பு I R இடைவெளியில் கொடுக்கப்படட்டும். F () சார்பு, எந்த I க்கும் F () = f () என்ற இடைவெளியில் f () செயல்பாட்டின் ஆண்டிடெரிவேட்டிவ் எனப்படும்.

மாஸ்கோ இன்ஸ்டிடியூட் ஆப் இயற்பியல் மற்றும் தொழில்நுட்ப மாநில பல்கலைக்கழகம்) ஓ.வி. பெசோவ் ட்ரைகோனோமெட்ரிக் ஃபோரியர் தொடர் கல்வி மற்றும் வழிமுறை கையேடு மாஸ்கோ, 004 தொகுத்தவர் பெசோவ் யுடிசி 517. முக்கோணவியல் தொடர்

8. சக்தித் தொடர் 8.. c n (z) n, (8.) n= வடிவத்தின் செயல்பாட்டுத் தொடர் c n என்பது ஒரு எண் வரிசை, R என்பது ஒரு நிலையான எண், மற்றும் z R என்பது c n குணகங்களைக் கொண்ட சக்தித் தொடர் என அழைக்கப்படுகிறது. . மாறிகளின் மாற்றத்தைச் செய்வதன் மூலம்

உயர் கணிதத்தின் கணிதம் மற்றும் கணினி அறிவியல் கூறுகள், தொலைதூரத் தொழில்நுட்பங்களைப் பயன்படுத்தி படிக்கும் இடைநிலைத் தொழிற்கல்வி மாணவர்களுக்கான கல்வி மற்றும் முறையியல் வளாகம் தொகுதி வேறுபட்ட கால்குலஸ் தொகுக்கப்பட்டது:

1. திட்டவட்டமான ஒருங்கிணைப்பு 1.1. f என்பது பிரிவு [, b] R இல் வரையறுக்கப்பட்ட ஒரு வரம்புக்குட்பட்ட செயல்பாடாக இருக்கட்டும். [, b] பிரிவின் ஒரு பகிர்வு என்பது τ = (x, x 1,..., x n 1, x n) [, b ] அத்தகைய = x< x 1 < < x n 1

"கணித பகுப்பாய்வு" என்ற பிரிவில் இறுதித் தேர்வுக்கான கேள்விகள் மற்றும் மாதிரி சிக்கல்கள் பயன்பாட்டுக் கணிதம் வாய்வழித் தேர்வில், மாணவர் இரண்டு தத்துவார்த்த கேள்விகளையும் இரண்டு சிக்கல்களையும் பெறுகிறார் ஆண்டுக்கு மொத்தம் 66 கேள்விகள்

தொகுதி தலைப்பு செயல்பாட்டு வரிசைகள் மற்றும் தொடர்களின் சீரான ஒருங்கிணைப்பின் பண்புகள் மற்றும் தொடர் பவர் தொடர் விரிவுரை செயல்பாட்டு வரிசைகள் மற்றும் தொடர்களின் வரையறைகள் சீராக

~ ~ காலவரையற்ற மற்றும் திட்டவட்டமான ஒருங்கிணைப்புகள் எதிர் வழித்தோன்றல் மற்றும் காலவரையற்ற ஒருங்கிணைப்பின் கருத்து. வரையறை: இந்தச் சார்புகள் பின்வருமாறு தொடர்புடையதாக இருந்தால், F சார்பு f இன் ஆண்டிடெரிவேடிவ் எனப்படும்

ரஷ்ய கூட்டமைப்பின் கல்வி மற்றும் அறிவியல் அமைச்சகம் ஃபெடரல் ஸ்டேட் பட்ஜெட் கல்வி நிறுவனம் உயர் தொழில்முறை கல்வி "சைபீரியன் மாநில தொழில்துறை பல்கலைக்கழகம்"

சதுர சமன்பாடுகள் உள்ளடக்கம் சதுர சமன்பாடுகள்... 4. மற்றும் இருபடி சமன்பாடுகளின் ஆய்வு... 4.. எண் குணகங்களுடன் இருபடி சமன்பாடு... 4.. இருபடி சமன்பாடுகளைத் தீர்த்து ஆய்வு செய்தல்

விமானப்படையின் இராணுவப் பயிற்சி மற்றும் அறிவியல் மையம் "பேராசிரியர் N. E. ZHUKOVSKY மற்றும் Y. A. GAGARIN ஆகியோரின் பெயரிடப்பட்ட வான் இராணுவ அகாடமி" N. G. AFENDIKOVA, I. N. OMELCHENKO, G ஒரு பகுப்பாய்வு எடுத்துக்காட்டுகள்

கல்விக்கான ஃபெடரல் ஏஜென்சி மாநில உயர் தொழில்முறை கல்வி நிறுவனம்

அத்தியாயம் 5. ஃபோரியர் தொடர் 5.. பாடம் 5 5... அடிப்படை வரையறைகள் a 2 + (a k cos x + b k si x) (5..) வடிவத்தின் செயல்பாட்டுத் தொடர் முக்கோணவியல் தொடர் எனப்படும், எண்கள் a மற்றும் b முக்கோணவியல் குணகங்கள்

ஃபோரியர் தொடர் ஆர்த்தோகனல் அமைப்புகளின் செயல்பாடுகள் இயற்கணிதத்தின் பார்வையில், கொடுக்கப்பட்ட வகுப்பின் செயல்பாடுகள் மற்றும் - R அல்லது C இலிருந்து குணகங்களின் சமத்துவம் என்பது வெக்டார் B இன் திசையன்களின் நேரியல் கலவையாகும்.

3724 பல தொடர்கள் மற்றும் வளைவு ஒருங்கிணைப்புகள் 1 பிரிவுகளின் வேலைத் திட்டம் “பல தொடர்கள் மற்றும் வளைவு ஒருங்கிணைப்புகள்” 11 எண் தொடர் எண் தொடரின் கருத்துரு எண் தொடரின் பண்புகள் ஒருங்கிணைப்பின் தேவையான அடையாளம்

ஒரு மாறுபாட்டின் செயல்பாடுகளின் வேறுபாடு, அதன் வடிவியல் மற்றும் இயற்பியல் பொருள், A x என்ற புள்ளியில் y f (x) வரையிலான டேன்ஜென்ட் S ஐ தீர்மானிக்கும் கருத்துக்கு வழிவகுக்கும். f (

வேறுபட்ட சமன்பாடுகள் 1. அடிப்படைக் கருத்துக்கள் ஒரு குறிப்பிட்ட செயல்பாட்டிற்கான வேறுபாடு சமன்பாடு என்பது இந்தச் சார்பை அதன் சார்பற்ற மாறிகள் மற்றும் அதன் வழித்தோன்றல்களுடன் இணைக்கும் சமன்பாடாகும்.

முதல் வரிசையின் சாதாரண வேறுபட்ட சமன்பாடுகள் அடிப்படைக் கருத்துக்கள் ஒரு சமன்பாடு ஆகும், இதில் ஒரு அறியப்படாத செயல்பாடு வழித்தோன்றல் அல்லது வேறுபாடு அடையாளத்தின் கீழ் தோன்றும்.

வேறுபட்ட சமன்பாடுகள் பொதுவான கருத்துக்கள் வேறுபட்ட சமன்பாடுகள் இயக்கவியல், இயற்பியல், வானியல், தொழில்நுட்பம் மற்றும் உயர் கணிதத்தின் பிற கிளைகளில் (உதாரணமாக) பல மற்றும் மாறுபட்ட பயன்பாடுகளைக் கொண்டுள்ளன

செயல்பாட்டுத் தொடர் செயல்பாட்டுத் தொடர், அதன் கூட்டுத்தொகை மற்றும் செயல்பாட்டுக் களம் o உண்மையான அல்லது சிக்கலான எண்களின் (k 1 A செயல்பாட்டுத் தொடர் எனப்படும்) டொமைனில் k (k 1) செயல்பாடுகளின் வரிசை கொடுக்கப்பட வேண்டும்.

ஆர்த்தோகனல் பாலினோமியல்களின் அமைப்புகள் மற்றும் அவற்றின் பயன்பாடுகள் ஏ. செபிஷேவ் - ஹெர்மைட் பல்லுறுப்புக்கோவைகள் அறிமுகக் குறிப்புகள் கணித இயற்பியல், குவாண்டம் இயக்கவியல், கோட்பாட்டு இயற்பியல் ஆகியவற்றின் பல முக்கியமான சிக்கல்களைத் தீர்க்கும்போது அது அவசியம்

அசோசியேட் பேராசிரியர் முசினா எம்வி தயாரித்த விரிவுரைகள் எண் மற்றும் செயல்பாட்டுத் தொடர் எண் தொடர்: அடிப்படைக் கருத்துக்கள் (), ஒரு எண் தொடர் (அல்லது வெறுமனே ஒரு தொடர்) எண்கள், தொடரின் உறுப்பினர்கள் (சார்ந்திருக்கும்