வீடு→பிளம்பிங், வெப்பமூட்டும்→செயல்பாடுகளின் தொடர்ச்சி. தொடர்ச்சியான செயல்பாடுகள்

செயல்பாடுகளின் தொடர்ச்சி. தொடர்ச்சியான செயல்பாடுகள்

தொடர்ச்சியான செயல்பாடுகள்கணித பகுப்பாய்வு செயல்படும் செயல்பாடுகளின் முக்கிய வகுப்பை உருவாக்குகிறது. தொடர்ச்சியான செயல்பாட்டின் ஒரு யோசனை அதன் வரைபடம் தொடர்ச்சியானது என்று கூறுவதன் மூலம் பெறலாம், அதாவது. காகிதத்தில் இருந்து பென்சிலை எடுக்காமல் வரையலாம்.

ஒரு தொடர்ச்சியான செயல்பாடு, நடைமுறையில் நாம் அடிக்கடி சந்திக்கும் ஒரு சொத்தை கணித ரீதியாக வெளிப்படுத்துகிறது, அதாவது ஒரு சுயாதீன மாறியில் ஒரு சிறிய அதிகரிப்பு ஒரு சார்பு மாறியில் (செயல்பாடு) ஒரு சிறிய அதிகரிப்புக்கு ஒத்திருக்கிறது. தொடர்ச்சியான செயல்பாட்டின் சிறந்த எடுத்துக்காட்டுகள் உடல்களின் இயக்கத்தின் பல்வேறு விதிகள் \(s=f(t)\), சரியான நேரத்தில் உடல் கடந்து செல்லும் பாதை \(s\) சார்ந்திருப்பதை வெளிப்படுத்துகிறது \(t\). நேரமும் இடமும் தொடர்ச்சியாக இருக்கும், அதே சமயம் உடல் இயக்கத்தின் ஒன்று அல்லது மற்றொரு விதி \(s=f(t)\) அவற்றுக்கிடையே ஒரு குறிப்பிட்ட தொடர்ச்சியான தொடர்பை ஏற்படுத்துகிறது, இது ஒரு சிறிய நேர அதிகரிப்பு பாதையின் சிறிய அதிகரிப்புக்கு ஒத்ததாக இருக்கும்.

மனிதன் தன்னைச் சுற்றியுள்ள தொடர்ச்சியான ஊடகங்கள் என்று அழைக்கப்படுவதைக் கவனிப்பதன் மூலம் தொடர்ச்சியின் சுருக்கத்திற்கு வந்தான் - திட, திரவ அல்லது வாயு, எடுத்துக்காட்டாக உலோகங்கள், நீர், காற்று. உண்மையில், இப்போது நன்கு அறியப்பட்டபடி, எந்தவொரு இயற்பியல் ஊடகமும் ஒன்றுக்கொன்று பிரிக்கப்பட்ட அதிக எண்ணிக்கையிலான நகரும் துகள்களின் குவிப்பு ஆகும். எவ்வாறாயினும், இந்த துகள்களும் அவற்றுக்கிடையேயான தூரங்களும் ஊடகங்களின் தொகுதிகளுடன் ஒப்பிடும்போது மிகவும் சிறியவை, அவை மேக்ரோஸ்கோபிக்கில் நாம் கையாள வேண்டும். உடல் நிகழ்வுகள், எந்த இடைவெளியும் இல்லாமல், அது ஆக்கிரமிக்கப்பட்ட இடத்தில் தொடர்ச்சியாக விநியோகிக்கப்படும், தோராயமாக ஆய்வு செய்யப்பட்ட ஊடகத்தின் வெகுஜனத்தை நாம் கருத்தில் கொண்டால், இதுபோன்ற பல நிகழ்வுகளை நன்றாகப் படிக்க முடியும். பல இயற்பியல் துறைகள் இந்த அனுமானத்தை அடிப்படையாகக் கொண்டவை, உதாரணமாக ஹைட்ரோடைனமிக்ஸ், ஏரோடைனமிக்ஸ் மற்றும் நெகிழ்ச்சி கோட்பாடு. தொடர்ச்சியின் கணிதக் கருத்து இயற்கையாகவே இந்த துறைகளில் பலவற்றில் ஒரு பெரிய பாத்திரத்தை வகிக்கிறது.

சில செயல்பாடு \(y=f(x)\) மற்றும் சுயாதீன மாறியின் நன்கு வரையறுக்கப்பட்ட மதிப்பு \(x_0\) . எங்கள் செயல்பாடு சில தொடர்ச்சியான செயல்முறைகளை பிரதிபலிக்கிறது என்றால், \(x_0\) இலிருந்து சிறிது வேறுபடும் \(x\) மதிப்புகள், செயல்பாட்டின் மதிப்புகள் \(f(x)\) இலிருந்து சிறிது வேறுபடும் \(x_0\) புள்ளியில் \(f(x_0)\) மதிப்பு. எனவே, சுயாதீன மாறியின் அதிகரிப்பு \(x-x_0\) சிறியதாக இருந்தால், செயல்பாட்டின் தொடர்புடைய அதிகரிப்பு \(f(x)-f(x_0)\) சிறியதாக இருக்க வேண்டும். வேறு வார்த்தைகளில் கூறுவதானால், \(x-x_0\) இன் இன்கிரிமென்ட் பூஜ்ஜியமாக இருந்தால், செயல்பாட்டின் அதிகரிப்பு \(f(x)-f(x_0)\) பூஜ்ஜியமாக இருக்க வேண்டும், இது பின்வருமாறு எழுதப்படலாம்:

\(\lim_(x-x_0\to0)\Bigl=0.\)

இந்த உறவானது \(x_0\) புள்ளியில் ஒரு செயல்பாட்டின் தொடர்ச்சியின் கணித வரையறையாகும்.

சமத்துவம் (1) திருப்தி அடைந்தால் \(f(x)\) செயல்பாடு \(x_0\) புள்ளியில் தொடர்ச்சி என்று அழைக்கப்படுகிறது.

மற்றொரு வரையறையை வழங்குவோம்:

செயல்பாடு தொடர்புடைய அனைத்து மதிப்புகளுக்கும் தொடர்ச்சியானதாகக் கூறப்படுகிறது இந்த பிரிவு, இந்தப் பிரிவின் ஒவ்வொரு புள்ளியிலும் \(x_0\) தொடர்ச்சியாக இருந்தால், அதாவது. அத்தகைய ஒவ்வொரு புள்ளியிலும் சமத்துவம் (1) திருப்தி அடைகிறது.

எனவே, ஒரு செயல்பாட்டின் சொத்தின் கணித வரையறையை அறிமுகப்படுத்த, அதன் வரைபடம் ஒரு தொடர்ச்சியான (இந்த வார்த்தையின் வழக்கமான அர்த்தத்தில்) வளைவு என்பதை உள்ளடக்கியது, முதலில் உள்ளூர், உள்ளூர் சொத்தை தீர்மானிக்க வேண்டியது அவசியம். தொடர்ச்சி (புள்ளியில் தொடர்ச்சி \(x_0\) ), பின்னர், இந்த அடிப்படையில், முழுப் பகுதியிலும் செயல்பாட்டின் தொடர்ச்சியைத் தீர்மானிக்கவும்.

மேலே உள்ள வரையறை, கடந்த நூற்றாண்டின் தொடக்கத்தில் Cauchy மூலம் முதலில் சுட்டிக்காட்டப்பட்டது, பொதுவாக நவீனத்தில் ஏற்றுக்கொள்ளப்படுகிறது கணித பகுப்பாய்வு. பலவற்றைச் சரிபார்க்கிறது குறிப்பிட்ட உதாரணங்கள்இந்த வரையறை தொடர்ச்சியான செயல்பாட்டின் தற்போதைய நடைமுறைக் கருத்துடன் ஒத்துப்போகிறது, எடுத்துக்காட்டாக, தொடர்ச்சியான வரைபடத்தின் கருத்து.

தொடர்ச்சியான செயல்பாடுகளின் எடுத்துக்காட்டுகளில் பள்ளிக் கணிதம் \(x^n,\) \(\sin(x),\) \(\cos(x),\) \(a^x,\) \ ( \lg(x),\) \(\arcsin(x),\) \(\arccos(x)\) . பட்டியலிடப்பட்ட அனைத்து செயல்பாடுகளும் அவை வரையறுக்கப்பட்ட மாற்றத்தின் \(x\) இடைவெளியில் தொடர்ச்சியாக இருக்கும்.

தொடர்ச்சியான செயல்பாடுகளைச் சேர்த்தால், கழித்தால், பெருக்கி மற்றும் வகுத்தால் (பூஜ்ஜியத்திற்கு சமமாக இல்லாத ஒரு வகுப்போடு), அதன் விளைவாக நாம் மீண்டும் ஒரு தொடர்ச்சியான செயல்பாட்டிற்கு வருவோம். இருப்பினும், பிரிக்கும் போது, வழக்கமாக \(x_0\) மதிப்புகளுக்கு தொடர்ச்சி உடைக்கப்படுகிறது, இதில் வகுப்பில் உள்ள செயல்பாடு பூஜ்ஜியத்திற்கு செல்கிறது. பிரிவின் முடிவு \(x_0\) புள்ளியில் இடைவிடாத செயல்பாட்டைக் குறிக்கிறது.

\(y=\frac(1)(x)\) சார்பு \(y=0\) புள்ளியில் இடைவிடாத செயல்பாட்டிற்கு ஒரு எடுத்துக்காட்டு. தொடர்ச்சியற்ற செயல்பாடுகளின் பல எடுத்துக்காட்டுகள் படத்தில் காட்டப்பட்டுள்ள வரைபடங்களால் கொடுக்கப்பட்டுள்ளன. 1.

இந்த வரைபடங்களை கவனமாக மதிப்பாய்வு செய்ய பரிந்துரைக்கிறோம். செயல்பாடுகளின் இடைநிறுத்தங்கள் வேறுபட்டவை என்பதை நினைவில் கொள்ளவும்: சில நேரங்களில் \(x\) புள்ளியை \(x_0\) அணுகும்போது, செயல்பாடு நிறுத்தப்படும்போது, \(f(x)\) வரம்பு உள்ளது, ஆனால் \(f இலிருந்து வேறுபட்டது. (x_0)\ ), மற்றும் சில நேரங்களில், படம். 1c, இந்த வரம்பு வெறுமனே இல்லை. ஒருபுறம் \(x\) \(x_0\) நெருங்கும் போது \(f(x)-f(x_0)\to0\) , மற்றும் \(x\ to x_0\) அணுகினால் மறுபுறம், பின்னர் \(f(x)-f(x_0)\) இனி பூஜ்ஜியமாக இருக்காது. இந்த விஷயத்தில், நிச்சயமாக, செயல்பாட்டின் இடைநிறுத்தம் எங்களிடம் உள்ளது, இருப்பினும் இந்த கட்டத்தில் அது "ஒரு பக்கத்தில் தொடர்ந்து உள்ளது" என்று நாம் கூறலாம். இந்த வழக்குகள் அனைத்தையும் கீழே உள்ள வரைபடங்களில் காணலாம்.

ஒரு செயல்பாட்டின் தொடர்ச்சியின் வரையறை

1. \(y=f(x)\) செயல்பாடு \(x=a\) புள்ளியில் தொடர்ந்து இருக்கும் இடது மற்றும் வலதுபுறத்தில் உள்ள வரம்புகள் இந்த கட்டத்தில் செயல்பாட்டின் மதிப்புக்கு சமமாகவும் சமமாகவும் இருந்தால், அதாவது.

\(\lim_(x\to a-0)f(x)=\lim_(x\to a+0)f(x)=f(a).\)

2. செயல்பாடு \(y=f(x)\) இந்த புள்ளியில் வரையறுக்கப்பட்டால் \(x=a\) புள்ளியில் தொடர்ச்சியாக இருக்கும் மற்றும் வாதத்தில் ஒரு எண்ணற்ற அதிகரிப்பு செயல்பாட்டின் எல்லையற்ற அதிகரிப்புக்கு ஒத்ததாக இருந்தால், அதாவது \(\lim_(\Delta x\to 0)\Delta y=0\)புள்ளிக்கு அருகில் \(a\) .

வரையறுக்கப்பட்ட எண்ணிக்கையிலான தொடர்ச்சியான செயல்பாடுகளின் கூட்டுத்தொகை, வேறுபாடு மற்றும் பலன் ஒரு தொடர்ச்சியான செயல்பாடு ஆகும்.

\(\) ஒரு இடைவெளியில் தொடர்ச்சியான செயல்பாடு அதன் சிறிய \(m\) மற்றும் பெரிய \(M\) மதிப்புக்கு இடையில் ஏதேனும் இடைநிலை மதிப்பை எடுக்கும், அதாவது \(m\leqslant f(x)\leqslant M\)அனைவருக்கும் \(x\in\) . பிரிவின் எல்லைப் புள்ளிகளில் இருந்தால் \(\) செயல்பாடு உள்ளது வெவ்வேறு அறிகுறிகள், பின்னர் பிரிவின் உள்ளே உள்ளன குறைந்தபட்சம்அத்தகைய ஒரு மதிப்பு \(x=c\) இதில் செயல்பாடு பூஜ்ஜியமாக மாறும். செயல்பாடுகளின் தொடர்ச்சியின் இந்த பண்பு பல்லுறுப்புக்கோவைகளின் வேர்களை தோராயமாக கண்டுபிடிக்க அனுமதிக்கிறது.

செயல்பாடு முறிவு புள்ளிகள்

தொடர்ச்சியான நிபந்தனைகளை பூர்த்தி செய்யாத வாத மதிப்புகள் அழைக்கப்படுகின்றன செயல்பாடு முறிவு புள்ளிகள். இந்த வழக்கில், இரண்டு வகையான செயல்பாடு இடைநிறுத்த புள்ளிகள் வேறுபடுகின்றன.

இடதுபுறத்தில் \(x\to a\) என்றால் செயல்பாடு உள்ளது இறுதி வரம்பு\(k_1\) , மற்றும் வலதுபுறத்தில் உள்ள \(x\to a\) செயல்பாட்டிற்கு வரையறுக்கப்பட்ட வரம்பு \(k_2\) மற்றும் \(k_1\ne k_2\) , பின்னர் \(x க்கான செயல்பாடு என்று கூறுகிறார்கள். =a\) உள்ளது முதல் வகையான முறிவு. \(|k_1-k_2|\) வேறுபாடு \(x=a\) புள்ளியில் செயல்பாட்டின் தாவலை தீர்மானிக்கிறது. \(x=a\) இல் உள்ள செயல்பாட்டின் மதிப்பு எந்த எண்ணுக்கும் சமமாக இருக்கும் \(k_3\) .

\(x=a\) இல் உள்ள ஒரு செயல்பாட்டின் மதிப்பு \(k_1\) க்கு சமமாக இருந்தால், செயல்பாடு தொடர்ந்து விடப்படும் என்று கூறப்படுகிறது; \(k_2\) என்றால், செயல்பாடு சரியான தொடர்ச்சியானது என்று கூறுகிறார்கள்.

\(k_1=k_2\ne k_3\) எனில், செயல்பாடு \(a\) புள்ளியில் உள்ளது என்று கூறுகிறார்கள். சரிசெய்யக்கூடிய இடைவெளி.

வலது அல்லது இடதுபுறத்தில் \(x\ to a\) இல் இருந்தால், செயல்பாட்டின் வரம்பு இல்லை அல்லது முடிவிலிக்கு சமமாக இருந்தால், அதாவது \(\lim_(x\to a)f(x)=\infty \), பின்னர் at \ (x=a\) செயல்பாடு உள்ளது என்று கூறுகிறார்கள் இரண்டாவது வகையான இடைநிறுத்தம்.

எடுத்துக்காட்டு 1. \(x\) செயல்பாடு \(y=x^3-2x\) தொடர்ச்சியாக இருக்கும் மதிப்புகளின் தொகுப்பைக் கண்டறியவும்.

தீர்வு. செயல்பாட்டின் அதிகரிப்பைக் கண்டுபிடிப்போம்

\(\Delta y=(x+\Delta x)^3-2(x+\Delta x)-(x^3-2x)=\Delta x\,(\Delta x^2+3x\Delta x+3x^ 2-2).\)

\(\Delta x\to0\) மாறி \(x\) மாறியின் எந்த மதிப்புகளுக்கும் அதிகரிப்பு \(\Delta y\to0\) ஆகும், எனவே மாறியின் அனைத்து உண்மையான மதிப்புகளுக்கும் செயல்பாடு தொடர்ச்சியாக இருக்கும். (x\) .

எடுத்துக்காட்டு 2. \(y=\frac(1)(x-1)\) செயல்பாட்டின் தொடர்ச்சியை \(x=3\) புள்ளியில் நிரூபிக்கவும்.

தீர்வு. இதை நிரூபிக்க, வாதத்தின் மதிப்பு \(x=3\) இலிருந்து \(x=3+\Delta x\)க்கு நகரும் போது \(y\) செயல்பாட்டின் அதிகரிப்பைக் கண்டுபிடிப்போம்.

\(\Delta y=\frac(1)(3+\Delta x-1)-\frac(1)(3-1)=\frac(1)(2+\Delta x)-\frac(1) (2)=\frac(2-2-\Delta x)(2(2+\Delta x))=\frac(-\Delta x)(2(2+\Delta x)).\)

செயல்பாடு அதிகரிப்பின் வரம்பை \(\Delta x\to0\) இல் காணலாம்

\(\lim_(\Delta x\to0)\Delta y=-\lim_(\Delta x\to0)\frac(\Delta x)(2(2+\Delta x))=-\frac(0)( 2(2+0))=0.\)

\(\Delta x\to0\) இல் உள்ள செயல்பாட்டின் அதிகரிப்பின் வரம்பு பூஜ்ஜியத்திற்கு சமமாக இருப்பதால், \(x\to3\) இல் உள்ள செயல்பாடு தொடர்ச்சியாக இருக்கும்.

எடுத்துக்காட்டு 3. செயல்பாடுகளின் தொடர்ச்சியின் தன்மையைத் தீர்மானித்தல் மற்றும் வரைபடங்களை உருவாக்குதல்:

\(\mathrm(a))~y=\frac(1)(x-1)~\text(if)~x=1;\qquad\mathrm(b))~y=\frac(x)(| x|)~\ text(if)~x=0;\qquad\mathrm(c))~y=\begin(cases)2x,&\text(if)~x\ne2,\\1,&\text (என்றால்)~x=2;\முடிவு(வழக்குகள்)\qquad\mathrm(d))~y=a^(1/x)~(a>1);\qquad\mathrm(e))~y=\ ஆபரேட்டர் பெயர்(arctg)\frac(1)(x).\)

தீர்வு.

அ) \(x=1\) செயல்பாடு வரையறுக்கப்படாதபோது, இந்த கட்டத்தில் ஒருபக்க வரம்புகளைக் காண்கிறோம்:

\(\lim_(x\to1-0)\frac(1)(x-1)=-\infty;\quad\lim_(x\to1+0)\frac(1)(x-1)=+\ infty.\)

இதன் விளைவாக, \(x=1\) புள்ளியில் செயல்பாடு இரண்டாவது வகையான இடைநிறுத்தத்தைக் கொண்டுள்ளது.

b) \(x<0\) предел функции равен \(\lim_(0-0)\frac(x)(|x|)=-1=k_1\). \(x>0\) வரம்பு சமமாக இருக்கும்போது \(\lim_(0+0)\frac(x)(|x|)=1=k_2\). இதன் விளைவாக, \(x=1\) புள்ளியில் \(y\) சார்பு முதல் வகையின் தொடர்ச்சியற்ற தன்மையைக் கொண்டுள்ளது மற்றும் செயல்பாட்டின் ஜம்ப் \(|k_1-k_2|=|-1-1|= க்கு சமமாக இருக்கும். 2\) .

c) செயல்பாடு முழு எண் அச்சில் வரையறுக்கப்படுகிறது, அடிப்படை அல்லாதது, ஏனெனில் \(x=2\) புள்ளியில் செயல்பாட்டின் பகுப்பாய்வு வெளிப்பாடு மாறுகிறது. செயல்பாட்டின் தொடர்ச்சியை \(x=2\) புள்ளியில் ஆராய்வோம் :

\(\lim_(x\to2-0)=4,\quad\lim_(x\to2+0)2x=4,\quad y(2)=1,\quad k_1=k_2\ne k_3.\)

\(x=2\) என்ற புள்ளியில் செயல்பாடு நீக்கக்கூடிய இடைநிறுத்தத்தை கொண்டுள்ளது என்பது தெளிவாகிறது.

ஈ) \(x=0\) புள்ளியில் செயல்பாட்டின் இடது மற்றும் வலது வரம்புகளைக் கண்டறியவும்:

\(y(+0)=\lim_(x\to+0)a^(1/x)=+\infty,\quad y(-0)=\lim_(x\to-0)a^(1 /x)=0.\)

எனவே, புள்ளியில் \(x=0\) செயல்பாடு வலதுபுறத்தில் இரண்டாவது வகையான இடைநிறுத்தத்தையும், இடதுபுறத்தில் தொடர்ச்சியையும் கொண்டுள்ளது.

இ) செயல்பாட்டின் ஒருபக்க வரம்புகளை \(x=0\) புள்ளியில் கண்டறியவும்:

\(y(+0)=\lim_(x\to+0)\operatorname(arctg)\frac(1)(x)=\frac(\pi)(2),\quad y(-0)=\ lim_(x\to-0)\operatorname(arctg)\frac(1)(x)=-\frac(\pi)(2).\)

எனவே, செயல்பாட்டின் இருபுறமும் \(x=0\) புள்ளியில் \(y=\operatorname(arctg)\frac(1)(x)\)குதிரை பந்தயம்

உங்கள் உலாவியில் Javascript முடக்கப்பட்டுள்ளது.
கணக்கீடுகளைச் செய்ய, நீங்கள் ActiveX கட்டுப்பாடுகளை இயக்க வேண்டும்!

வரையறை. y = f(x) சார்பு x0 புள்ளியிலும் அதன் சில பகுதிகளிலும் வரையறுக்கப்படட்டும். y = f(x) சார்பு அழைக்கப்படுகிறது புள்ளி x0 இல் தொடர்ச்சி, என்றால்:

1. உள்ளது
2. இந்த வரம்பு x0 புள்ளியில் உள்ள செயல்பாட்டின் மதிப்புக்கு சமம்:

வரம்பை வரையறுக்கும் போது, f(x) என்பது x0 புள்ளியில் வரையறுக்கப்படாமல் போகலாம் என்றும், இந்த கட்டத்தில் வரையறுக்கப்பட்டால், f(x0) இன் மதிப்பு வரம்பை நிர்ணயிப்பதில் எந்த வகையிலும் பங்கேற்காது என்றும் வலியுறுத்தப்பட்டது. தொடர்ச்சியைத் தீர்மானிக்கும் போது, f(x0) இருப்பது அடிப்படையானது, மேலும் இந்த மதிப்பு lim f(x) க்கு சமமாக இருக்க வேண்டும்.

வரையறை. y = f(x) சார்பு x0 புள்ளியிலும் அதன் சில பகுதிகளிலும் வரையறுக்கப்படட்டும். அனைத்து ε>0க்கும் இருந்தால் x0 புள்ளியில் f(x) சார்பு தொடர்ச்சி என்று அழைக்கப்படுகிறது நேர்மறை எண்δ அதாவது x0 புள்ளியின் δ-அருகில் உள்ள அனைத்து x க்கும் (அதாவது |x-x0|
வரம்பின் மதிப்பு f(x0) க்கு சமமாக இருக்க வேண்டும் என்பது இங்கே கணக்கில் எடுத்துக்கொள்ளப்படுகிறது, எனவே, வரம்பின் வரையறையுடன் ஒப்பிடுகையில், δ-அருகிலுள்ள 0 ஐ துளையிடும் நிபந்தனை அகற்றப்பட்டது.
அதிகரிப்புகளின் அடிப்படையில் மேலும் ஒரு (முந்தையதற்கு சமமான) வரையறையை வழங்குவோம். Δх = x - x0 ஐக் குறிப்போம், இந்த மதிப்பை வாதத்தின் அதிகரிப்பு என்று அழைப்போம். x->x0, பின்னர் Δx->0, அதாவது Δx - b.m. (எல்லையற்ற) அளவு. Δу = f(x)-f(x0) ஐக் குறிப்போம், இந்த மதிப்பை செயல்பாட்டின் அதிகரிப்பு என்று அழைப்போம், ஏனெனில் |Δу| (போதுமான அளவு சிறியது |Δх|) தன்னிச்சையான எண் ε>0 ஐ விட குறைவாக இருக்க வேண்டும், பிறகு Δу- என்பது பி.எம். மதிப்பு, எனவே

வரையறை. y = f(x) சார்பு x0 புள்ளியிலும் அதன் சில பகுதிகளிலும் வரையறுக்கப்படட்டும். செயல்பாடு f(x) என்று அழைக்கப்படுகிறது புள்ளி x0 இல் தொடர்ச்சி, வாதத்தில் ஒரு எல்லையற்ற அதிகரிப்பு செயல்பாட்டில் உள்ள ஒரு எண்ணற்ற அதிகரிப்புக்கு ஒத்ததாக இருந்தால்.

வரையறை. x0 புள்ளியில் தொடர்ச்சியாக இல்லாத செயல்பாடு f(x), இடைவிடாது என்று அழைக்கப்படுகிறதுஇந்த கட்டத்தில்.

வரையறை.இந்த தொகுப்பின் ஒவ்வொரு புள்ளியிலும் தொடர்ச்சியாக இருந்தால், X தொகுப்பில் f(x) செயல்பாடு தொடர்ச்சி என்று அழைக்கப்படுகிறது.

ஒரு தொகை, தயாரிப்பு, பங்கு ஆகியவற்றின் தொடர்ச்சி பற்றிய தேற்றம்

தொடர்ச்சியான செயல்பாட்டின் அடையாளத்தின் கீழ் வரம்பிற்கு செல்லும் பாதையின் தேற்றம்

தொடர்ச்சியான செயல்பாடுகளின் சூப்பர்போசிஷனின் தொடர்ச்சி பற்றிய தேற்றம்

f(x) சார்பு ஒரு இடைவெளியில் வரையறுக்கப்பட்டு, இந்த இடைவெளியில் ஒரே மாதிரியாக இருக்கட்டும். பின்னர் f(x) இந்த பிரிவில் முதல் வகையான தொடர்ச்சியற்ற புள்ளிகளை மட்டுமே கொண்டிருக்க முடியும்.

இடைநிலை மதிப்பு தேற்றம். f(x) சார்பு ஒரு பிரிவில் தொடர்ச்சியாக இருந்து, இரண்டு புள்ளிகளில் a மற்றும் b (a என்பது b ஐ விடக் குறைவாக இருந்தால்) A = f(a) ≠ B = f(b), எந்த எண்ணுக்கும் C A மற்றும் B க்கு இடையில் ஒரு புள்ளி c ∈ உள்ளது, இதில் செயல்பாட்டின் மதிப்பு C: f(c) = C.

ஒரு இடைவெளியில் தொடர்ச்சியான செயல்பாட்டின் எல்லை பற்றிய தேற்றம்.ஒரு சார்பு f(x) ஒரு இடைவெளியில் தொடர்ச்சியாக இருந்தால், அது இந்த இடைவெளியில் வரம்பிடப்படும்.

குறைந்தபட்ச மற்றும் அதிகபட்ச மதிப்புகளை அடைவதற்கான தேற்றம். f(x) செயல்பாடு ஒரு இடைவெளியில் தொடர்ச்சியாக இருந்தால், அது இந்த இடைவெளியில் அதன் கீழ் மற்றும் மேல் எல்லைகளை அடைகிறது.

தலைகீழ் செயல்பாட்டின் தொடர்ச்சி பற்றிய தேற்றம். y=f(x) சார்பு தொடர்ச்சியாக இருக்கட்டும் மற்றும் [a,b] இடைவெளியில் கண்டிப்பாக அதிகரித்து (குறைகிறது). பின்னர் பிரிவில் ஒரு தலைகீழ் செயல்பாடு உள்ளது x = g(y), மேலும் சலிப்பான முறையில் அதிகரித்து (குறைந்து) ஆன் மற்றும் தொடர்கிறது.

இரண்டு செயல்பாடுகளைக் கருத்தில் கொள்வோம், அவற்றின் வரைபடங்கள் படத்தில் காட்டப்பட்டுள்ளன. 1 மற்றும் 2. முதல் செயல்பாட்டின் வரைபடத்தை காகிதத்தில் இருந்து பென்சிலை உயர்த்தாமல் வரையலாம். இந்த செயல்பாட்டை தொடர்ச்சி என்று அழைக்கலாம். இது போன்ற மற்றொரு செயல்பாட்டின் வரைபடத்தை வரைய முடியாது. இது இரண்டு தொடர்ச்சியான துண்டுகளைக் கொண்டுள்ளது, மேலும் ஒரு கட்டத்தில் அது ஒரு இடைநிறுத்தத்தைக் கொண்டுள்ளது, மேலும் செயல்பாட்டைத் தொடர்ச்சியற்றது என்று அழைப்போம்.

தொடர்ச்சியின் இத்தகைய காட்சி வரையறை கணிதத்திற்கு எந்த வகையிலும் பொருந்தாது, ஏனெனில் இது "பென்சில்" மற்றும் "காகிதம்" என்ற முற்றிலும் கணிதமற்ற கருத்துகளைக் கொண்டுள்ளது. தொடர்ச்சியின் சரியான கணித வரையறை வரம்பு என்ற கருத்தின் அடிப்படையில் கொடுக்கப்பட்டுள்ளது மற்றும் பின்வருமாறு.

ஒரு பிரிவில் ஒரு செயல்பாடு வரையறுக்கப்பட்டு இந்த பிரிவின் சில புள்ளியாக இருக்கட்டும். ஒரு செயல்பாடு ஒரு கட்டத்தில் தொடர்ச்சியானது என அழைக்கப்படுகிறது, அது (பிரிவில் இருந்து மட்டுமே கருதப்படுகிறது), செயல்பாட்டின் மதிப்புகள் முனைகின்றன, அதாவது. என்றால்

. (1)

ஒரு செயல்பாடு ஒவ்வொரு புள்ளியிலும் தொடர்ச்சியாக இருந்தால் ஒரு பிரிவில் தொடர்ச்சி என்று அழைக்கப்படுகிறது.

சமத்துவம் (1) ஒரு புள்ளியில் திருப்தி அடையவில்லை என்றால், செயல்பாடு புள்ளியில் இடைவிடாது என்று அழைக்கப்படுகிறது.

நாம் பார்ப்பது போல், கணித ரீதியாக, ஒரு பிரிவில் ஒரு செயல்பாட்டின் தொடர்ச்சியின் சொத்து ஒரு கட்டத்தில் தொடர்ச்சியின் உள்ளூர் சொத்து மூலம் தீர்மானிக்கப்படுகிறது.

மதிப்பு வாதத்தின் அதிகரிப்பு என்று அழைக்கப்படுகிறது, செயல்பாட்டின் மதிப்புகளுக்கு இடையிலான வேறுபாடு செயல்பாட்டின் அதிகரிப்பு என்று அழைக்கப்படுகிறது மற்றும் ஆல் குறிக்கப்படுகிறது. வெளிப்படையாக, வாதத்தின் போக்கில், அதிகரிப்பு பூஜ்ஜியமாக இருக்கும்: .

சமத்துவத்தை (1) சமமான வடிவத்தில் மீண்டும் எழுதுவோம்

அறிமுகப்படுத்தப்பட்ட குறியீட்டைப் பயன்படுத்தி, அதை பின்வருமாறு மீண்டும் எழுதலாம்:

எனவே, செயல்பாடு தொடர்ச்சியாக இருந்தால், வாதத்தின் அதிகரிப்பு பூஜ்ஜியமாக இருப்பதால், செயல்பாட்டின் அதிகரிப்பு பூஜ்ஜியமாக இருக்கும். அவர்கள் மற்றொரு வழியையும் கூறுகிறார்கள்: வாதத்தில் ஒரு சிறிய அதிகரிப்பு செயல்பாட்டில் ஒரு சிறிய அதிகரிப்புக்கு ஒத்திருக்கிறது. படத்தில். படம் 3, ஒரு கட்டத்தில் தொடர்ச்சியான செயல்பாட்டின் வரைபடத்தைக் காட்டுகிறது; படத்தில். 4 அதிகரிப்பு என்பது செயல்பாட்டின் அத்தகைய அதிகரிப்புக்கு ஒத்திருக்கிறது, அது எவ்வளவு சிறியதாக இருந்தாலும், பிரிவின் நீளத்தின் பாதிக்கு குறைவாக இருக்காது; செயல்பாடு புள்ளியில் இடைவிடாது உள்ளது.

காகிதத்திலிருந்து பென்சிலைத் தூக்காமல் வரைபடத்தை வரையக்கூடிய ஒரு செயல்பாடாக தொடர்ச்சியான செயல்பாட்டைப் பற்றிய எங்கள் யோசனை, கணித பகுப்பாய்வில் நிரூபிக்கப்பட்ட தொடர்ச்சியான செயல்பாடுகளின் பண்புகளால் முழுமையாக உறுதிப்படுத்தப்படுகிறது. எடுத்துக்காட்டாக, அவற்றின் பின்வரும் பண்புகளை நாம் கவனிக்கலாம்.

1. ஒரு பிரிவில் தொடர்ச்சியான செயல்பாடு, பிரிவின் முனைகளில் வெவ்வேறு குறிகளின் மதிப்புகளை எடுத்தால், இந்த பிரிவின் சில புள்ளியில் அது பூஜ்ஜியத்திற்கு சமமான மதிப்பை எடுக்கும்.

2. செயல்பாடு, இடைவெளியில் தொடர்ச்சியானது, எல்லாவற்றையும் எடுக்கும் இடைநிலை மதிப்புகள்இறுதி புள்ளிகளில் உள்ள மதிப்புகளுக்கு இடையில், அதாவது. மற்றும் இடையே.

3. ஒரு செயல்பாடு ஒரு பிரிவில் தொடர்ச்சியாக இருந்தால், இந்த பிரிவில் அது அதன் அதிகபட்ச மற்றும் அதன் அளவை அடைகிறது குறைந்த மதிப்பு, அதாவது பிரிவில் உள்ள செயல்பாட்டின் சிறிய மதிப்பு மற்றும் a என்பது மிகப்பெரிய மதிப்பு என்றால், இந்த பிரிவில் புள்ளிகள் மற்றும் போன்றவை உள்ளன.

இந்த அறிக்கைகளில் முதல் வடிவியல் பொருள் முற்றிலும் தெளிவாக உள்ளது: ஒரு தொடர்ச்சியான வளைவு ஒரு அச்சின் ஒரு பக்கத்திலிருந்து மற்றொன்றுக்கு சென்றால், அது இந்த அச்சை வெட்டுகிறது (படம் 5). ஒரு தொடர்ச்சியற்ற செயல்பாட்டிற்கு இந்த சொத்து இல்லை, இது படத்தில் உள்ள செயல்பாட்டின் வரைபடத்தால் உறுதிப்படுத்தப்படுகிறது. 2, அத்துடன் பண்புகள் 2 மற்றும் 3. படத்தில். மற்றும் இடையே இணைக்கப்பட்டிருந்தாலும், 2 செயல்பாடு மதிப்பை எடுக்காது. படத்தில். படம் 6 தொடர்ச்சியற்ற செயல்பாட்டின் உதாரணத்தைக் காட்டுகிறது ( பகுதியளவுஎண்), அதன் மிகப்பெரிய மதிப்பை அடையவில்லை.

அதே பிரிவில் தொடர்ச்சியான செயல்பாடுகளின் கூட்டல், கழித்தல், பெருக்கல் மீண்டும் தொடர்ச்சியான செயல்பாடுகளுக்கு வழிவகுக்கும். இரண்டு தொடர்ச்சியான செயல்பாடுகளைப் பிரிக்கும் போது, எல்லா இடங்களிலும் வகுப்பு பூஜ்ஜியமாக இல்லாமல் இருந்தால், விளைவு தொடர்ச்சியான செயல்பாடு ஆகும்.

கணிதம், முதலில், பல்வேறு இயக்க விதிகளைப் படிப்பதன் மூலம் தொடர்ச்சியான செயல்பாட்டின் கருத்துக்கு வந்தது. இடமும் நேரமும் தொடர்ச்சியானது, எடுத்துக்காட்டாக, ஒரு சட்டத்தால் வெளிப்படுத்தப்படும் நேரத்தின் பாதையின் சார்பு, தொடர்ச்சியான செயல்பாட்டின் உதாரணத்தை வழங்குகிறது.

திடப்பொருட்கள், திரவங்கள் மற்றும் வாயுக்களில் நிலைகள் மற்றும் செயல்முறைகளை விவரிக்க தொடர்ச்சியான செயல்பாடுகள் பயன்படுத்தப்படுகின்றன. அவற்றைப் படிக்கும் அறிவியல் - நெகிழ்ச்சி, ஹைட்ரோடினமிக்ஸ் மற்றும் ஏரோடைனமிக்ஸ் கோட்பாடு - "தொடர்ச்சியான இயக்கவியல்" என்ற பெயரில் ஒன்றுபட்டுள்ளன.

செயல்பாட்டின் தொடர்ச்சி. முறிவு புள்ளிகள்.

காளை நடக்கும்போது, ஆடுகிறது, பெருமூச்சு விடுகிறது:
- ஓ, பலகை தீர்ந்து வருகிறது, இப்போது நான் விழப் போகிறேன்!

அன்று இந்த பாடம்ஒரு செயல்பாட்டின் தொடர்ச்சி, இடைநிறுத்தப் புள்ளிகளின் வகைப்பாடு மற்றும் ஒரு பொதுவான நடைமுறைச் சிக்கல் ஆகியவற்றை நாங்கள் பகுப்பாய்வு செய்வோம் செயல்பாடுகளின் தொடர்ச்சியான ஆய்வுகள். தலைப்பின் பெயரிலிருந்தே, என்ன விவாதிக்கப்படும் என்று பலர் உள்ளுணர்வாக யூகித்து, பொருள் மிகவும் எளிமையானது என்று நினைக்கிறார்கள். இது உண்மைதான். ஆனால் புறக்கணிப்பு மற்றும் அவற்றைத் தீர்ப்பதற்கான மேலோட்டமான அணுகுமுறைக்கு பெரும்பாலும் தண்டிக்கப்படும் எளிய பணிகள் இது. எனவே, நீங்கள் கட்டுரையை மிகவும் கவனமாகப் படித்து அனைத்து நுணுக்கங்களையும் நுட்பங்களையும் பிடிக்க பரிந்துரைக்கிறேன்.

நீங்கள் என்ன தெரிந்து கொள்ள வேண்டும் மற்றும் செய்ய முடியும்?அதிகம் இல்லை. பாடத்தை நன்கு கற்க, அது என்ன என்பதை நீங்கள் புரிந்து கொள்ள வேண்டும் ஒரு செயல்பாட்டின் வரம்பு. உடன் வாசகர்கள் குறைந்த நிலைகட்டுரையைப் புரிந்துகொள்ள தயாரிப்பு போதுமானது செயல்பாட்டு வரம்புகள். தீர்வுகளின் எடுத்துக்காட்டுகள்மற்றும் கையேட்டில் உள்ள வரம்பின் வடிவியல் பொருளைப் பார்க்கவும் அடிப்படை செயல்பாடுகளின் வரைபடங்கள் மற்றும் பண்புகள். உங்களைப் பற்றி அறிந்து கொள்வதும் நல்லது வரைபடங்களின் வடிவியல் மாற்றங்கள், பெரும்பாலான சந்தர்ப்பங்களில் நடைமுறையில் ஒரு வரைபடத்தை உருவாக்குவது அடங்கும். வாய்ப்புகள் அனைவருக்கும் நம்பிக்கையானவை, மேலும் ஒரு முழு கெட்டில் கூட அடுத்த அல்லது இரண்டு மணிநேரங்களில் பணியைச் சமாளிக்க முடியும்!

செயல்பாட்டின் தொடர்ச்சி. முறிவு புள்ளிகள் மற்றும் அவற்றின் வகைப்பாடு

செயல்பாட்டின் தொடர்ச்சியின் கருத்து

முழு எண் கோட்டிலும் தொடர்ச்சியாக இருக்கும் சில செயல்பாட்டைக் கருத்தில் கொள்வோம்:

அல்லது, இன்னும் சுருக்கமாகச் சொல்வதென்றால், நமது செயல்பாடு (உண்மையான எண்களின் தொகுப்பு) தொடர்கிறது.

தொடர்ச்சியின் "பிலிஸ்டைன்" அளவுகோல் என்ன? வெளிப்படையாக, ஒரு தொடர்ச்சியான செயல்பாட்டின் வரைபடத்தை காகிதத்தில் இருந்து பென்சிலை உயர்த்தாமல் வரையலாம்.

இந்த வழக்கில், இரண்டு எளிய கருத்துக்கள் தெளிவாக வேறுபடுத்தப்பட வேண்டும்: ஒரு செயல்பாட்டின் களம்மற்றும் செயல்பாட்டின் தொடர்ச்சி. பொதுவாக அது அதே விஷயம் இல்லை. உதாரணமாக:

இந்த செயல்பாடு முழு எண் வரியில் வரையறுக்கப்படுகிறது, அதாவது அனைவரும்"x" என்பதன் பொருள் "y" என்பதன் சொந்த அர்த்தத்தைக் கொண்டுள்ளது. குறிப்பாக, என்றால் . ஒரு செயல்பாட்டின் வரையறையின்படி, வாதத்தின் மதிப்பு அதற்கு ஒத்திருக்க வேண்டும் என்பதால், மற்ற புள்ளி நிறுத்தப்படும் என்பதை நினைவில் கொள்க. ஒரே விஷயம்செயல்பாட்டு மதிப்பு. இவ்வாறு, வரையறையின் களம்எங்கள் செயல்பாடு: .

எனினும் இந்த செயல்பாடு தொடர்ந்து இல்லை!அந்த நேரத்தில் அவள் கஷ்டப்படுகிறாள் என்பது தெளிவாகத் தெரிகிறது இடைவெளி. இந்த வார்த்தை மிகவும் புரிந்துகொள்ளக்கூடியது மற்றும் உண்மையில், இங்கே பென்சில் எப்படியும் காகிதத்தில் இருந்து கிழிக்கப்பட வேண்டும். சிறிது நேரம் கழித்து, முறிவு புள்ளிகளின் வகைப்பாட்டைப் பார்ப்போம்.

ஒரு புள்ளியில் மற்றும் ஒரு இடைவெளியில் ஒரு செயல்பாட்டின் தொடர்ச்சி

ஒரு வழியில் அல்லது வேறு கணித பிரச்சனைஒரு கட்டத்தில் ஒரு செயல்பாட்டின் தொடர்ச்சி, ஒரு இடைவெளியில் ஒரு செயல்பாட்டின் தொடர்ச்சி, ஒரு அரை இடைவெளி அல்லது ஒரு பிரிவில் ஒரு செயல்பாட்டின் தொடர்ச்சி பற்றி நாம் பேசலாம். அதாவது, "வெறும் தொடர்ச்சி" இல்லை- செயல்பாடு எங்காவது தொடர்ந்து இருக்கலாம். மற்ற எல்லாவற்றின் அடிப்படை "கட்டிட தொகுதி" செயல்பாட்டின் தொடர்ச்சி புள்ளியில் .

கணித பகுப்பாய்வின் கோட்பாடு "டெல்டா" மற்றும் "எப்சிலான்" சுற்றுப்புறங்களைப் பயன்படுத்தி ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் தொடர்ச்சியின் வரையறையை வழங்குகிறது, ஆனால் நடைமுறையில் பயன்பாட்டில் வேறுபட்ட வரையறை உள்ளது, அதில் நாம் கவனம் செலுத்துவோம்.

முதலில் நினைவில் கொள்வோம் ஒரு பக்க வரம்புகள்முதல் பாடத்தில் நம் வாழ்வில் வெடித்தவர் செயல்பாட்டு வரைபடங்கள் பற்றி. அன்றாட சூழ்நிலையைக் கவனியுங்கள்:

நாம் அச்சை புள்ளிக்கு அணுகினால் விட்டு(சிவப்பு அம்பு), பின்னர் "விளையாட்டுகளின்" தொடர்புடைய மதிப்புகள் அச்சில் புள்ளிக்கு (சிவப்பு அம்பு) செல்லும். கணித ரீதியாக, இந்த உண்மை பயன்படுத்தி சரி செய்யப்பட்டது இடது கை வரம்பு:

உள்ளீட்டில் கவனம் செலுத்துங்கள் ("x இடதுபுறத்தில் ka க்கு முனைகிறது" என்று படிக்கிறது). "கூட்டல்" "கழித்தல் பூஜ்யம்" குறிக்கிறது , அடிப்படையில் இதன் பொருள் நாம் இடது பக்கத்திலிருந்து எண்ணை நெருங்குகிறோம்.

இதேபோல், நீங்கள் "கா" என்ற புள்ளியை அணுகினால் சரி(நீல அம்பு), பின்னர் "விளையாட்டுகள்" அதே மதிப்புக்கு வரும், ஆனால் பச்சை அம்புக்குறியுடன், மற்றும் வலது கை வரம்புபின்வருமாறு வடிவமைக்கப்படும்:

"சேர்க்கை" குறிக்கிறது , மற்றும் நுழைவு கூறுகிறது: "x வலதுபுறத்தில் ka ஆக உள்ளது."

ஒரு பக்க வரம்புகள் வரையறுக்கப்பட்டதாகவும் சமமாகவும் இருந்தால்(எங்கள் விஷயத்தைப் போல): , பிறகு GENERAL லிமிட் என்று சொல்வோம். இது எளிது, பொதுவான வரம்பு எங்கள் "வழக்கம்" ஒரு செயல்பாட்டின் வரம்பு, ஒரு வரையறுக்கப்பட்ட எண்ணுக்கு சமம்.

செயல்பாடு வரையறுக்கப்படவில்லை என்றால் (வரைபடக் கிளையில் உள்ள கரும்புள்ளியைத் துளைக்கவும்), மேலே உள்ள கணக்கீடுகள் செல்லுபடியாகும். ஏற்கனவே பல முறை குறிப்பிட்டுள்ளபடி, குறிப்பாக கட்டுரையில் எல்லையற்ற செயல்பாடுகளில், வெளிப்பாடுகள் "x" என்று அர்த்தம் எல்லையற்ற நெருக்கமானபுள்ளியை நெருங்குகிறது முக்கியமில்லை, செயல்பாடு ஒரு குறிப்பிட்ட புள்ளியில் வரையறுக்கப்பட்டதா இல்லையா. நல்ல உதாரணம்செயல்பாடு பகுப்பாய்வு செய்யப்படும் போது, அடுத்த பத்தியில் தோன்றும்.

வரையறை: கொடுக்கப்பட்ட புள்ளியில் செயல்பாட்டின் வரம்பு அந்த புள்ளியில் உள்ள செயல்பாட்டின் மதிப்புக்கு சமமாக இருந்தால், ஒரு புள்ளியில் ஒரு செயல்பாடு தொடர்ச்சியாக இருக்கும்: .

வரையறை பின்வரும் சொற்களில் விவரிக்கப்பட்டுள்ளது:

1) செயல்பாடு புள்ளியில் வரையறுக்கப்பட வேண்டும், அதாவது மதிப்பு இருக்க வேண்டும்.

2) செயல்பாட்டின் பொதுவான வரம்பு இருக்க வேண்டும். மேலே குறிப்பிட்டுள்ளபடி, இது ஒரு பக்க வரம்புகளின் இருப்பு மற்றும் சமத்துவத்தை குறிக்கிறது: .

3) கொடுக்கப்பட்ட புள்ளியில் செயல்பாட்டின் வரம்பு இந்த கட்டத்தில் செயல்பாட்டின் மதிப்புக்கு சமமாக இருக்க வேண்டும்: .

மீறினால் குறைந்தது ஒன்றுஇருந்து மூன்று நிபந்தனைகள், பின்னர் செயல்பாடு புள்ளியில் தொடர்ச்சியின் சொத்தை இழக்கிறது.

ஒரு இடைவெளியில் செயல்பாட்டின் தொடர்ச்சிபுத்திசாலித்தனமாகவும் மிகவும் எளிமையாகவும் வடிவமைக்கப்பட்டுள்ளது: கொடுக்கப்பட்ட இடைவெளியின் ஒவ்வொரு புள்ளியிலும் தொடர்ச்சியாக இருந்தால், இடைவெளியில் ஒரு செயல்பாடு தொடர்கிறது.

குறிப்பாக, பல செயல்பாடுகள் எல்லையற்ற இடைவெளியில், அதாவது உண்மையான எண்களின் தொகுப்பில் தொடர்ச்சியாக இருக்கும். இது ஒரு நேரியல் சார்பு, பல்லுறுப்புக்கோவைகள், அதிவேக, சைன், கொசைன் போன்றவை. பொதுவாக, ஏதேனும் அடிப்படை செயல்பாடுஅதன் மீது தொடர்ந்து வரையறையின் களம், எனவே, உதாரணமாக, மடக்கை செயல்பாடுஇடைவெளியில் தொடர்கிறது. அடிப்படை செயல்பாடுகளின் வரைபடங்கள் எப்படி இருக்கும் என்பது பற்றி இப்போது உங்களுக்கு நல்ல யோசனை இருக்கும் என்று நம்புகிறேன். மேலும் விரிவான தகவல்அவற்றின் தொடர்ச்சியை இதிலிருந்து அறியலாம் அன்பான நபர்ஃபிச்சென்கோல்ட்ஸ் என்ற குடும்பப்பெயரால்.

ஒரு பிரிவு மற்றும் அரை இடைவெளியில் ஒரு செயல்பாட்டின் தொடர்ச்சியுடன், எல்லாம் கடினமாக இல்லை, ஆனால் வகுப்பில் இதைப் பற்றி பேசுவது மிகவும் பொருத்தமானது. ஒரு பிரிவில் செயல்பாட்டின் குறைந்தபட்ச மற்றும் அதிகபட்ச மதிப்புகளைக் கண்டறிவது பற்றி, ஆனால் இப்போதைக்கு அதைப் பற்றி கவலைப்பட வேண்டாம்.

இடைவேளை புள்ளிகளின் வகைப்பாடு

செயல்பாடுகளின் கவர்ச்சிகரமான வாழ்க்கை அனைத்து வகையான சிறப்பு புள்ளிகளிலும் நிறைந்துள்ளது, மேலும் இடைவேளை புள்ளிகள் அவர்களின் வாழ்க்கை வரலாற்றின் பக்கங்களில் ஒன்றாகும்.

குறிப்பு : ஒரு வேளை, நான் ஒரு அடிப்படைப் புள்ளியில் வசிப்பேன்: முறிவுப் புள்ளி எப்போதும் இருக்கும் ஒற்றை புள்ளி- "ஒரு வரிசையில் பல இடைவெளி புள்ளிகள்" இல்லை, அதாவது, "பிரேக் இன்டர்வெல்" என்று எதுவும் இல்லை.

இந்த புள்ளிகள் இரண்டாக பிரிக்கப்பட்டுள்ளன பெரிய குழுக்கள்: முதல் வகையான சிதைவுகள்மற்றும் இரண்டாவது வகையான சிதைவுகள். ஒவ்வொரு வகை இடைவெளிக்கும் அதன் சொந்த உள்ளது சிறப்பியல்பு அம்சங்கள்நாம் இப்போது பார்ப்போம்:

முதல் வகையின் தொடர்ச்சியற்ற புள்ளி

ஒரு கட்டத்தில் தொடர்ச்சியான நிபந்தனை மீறப்பட்டால் மற்றும் ஒரு பக்க வரம்புகள் வரையறுக்கப்பட்ட , பின்னர் அது அழைக்கப்படுகிறது முதல் வகையான தொடர்ச்சியின்மை.

மிகவும் நம்பிக்கையான வழக்குடன் ஆரம்பிக்கலாம். பாடத்தின் அசல் யோசனையின்படி, நான் கோட்பாட்டைச் சொல்ல விரும்பினேன் “இன் பொதுவான பார்வை”, ஆனால் பொருளின் யதார்த்தத்தை நிரூபிப்பதற்காக, குறிப்பிட்ட எழுத்துக்களுடன் விருப்பத்தை நான் தீர்த்தேன்.

சோகம், பின்னணியில் புதுமணத் தம்பதிகளின் புகைப்படம் நித்திய சுடர், ஆனால் பின்வரும் சட்டகம் பொதுவாக ஏற்றுக்கொள்ளப்படுகிறது. வரைபடத்தில் செயல்பாட்டின் வரைபடத்தை சித்தரிப்போம்:

இந்தச் செயல்பாடு புள்ளியைத் தவிர, முழு எண் கோட்டிலும் தொடர்கிறது. உண்மையில், வகுத்தல் பூஜ்ஜியத்திற்கு சமமாக இருக்க முடியாது. இருப்பினும், வரம்பின் அர்த்தத்திற்கு ஏற்ப, நம்மால் முடியும் எல்லையற்ற நெருக்கமானஇடது மற்றும் வலதுபுறத்தில் இருந்து "பூஜ்ஜியத்தை" அணுகவும், அதாவது, ஒருதலைப்பட்ச வரம்புகள் உள்ளன மற்றும், வெளிப்படையாக, ஒத்துப்போகின்றன:
(தொடர்ச்சியின் நிபந்தனை எண். 2 திருப்திகரமாக உள்ளது).

ஆனால் செயல்பாடு புள்ளியில் வரையறுக்கப்படவில்லை, எனவே, தொடர்ச்சியின் நிபந்தனை எண். 1 மீறப்படுகிறது, மேலும் இந்த கட்டத்தில் செயல்பாடு ஒரு இடைநிறுத்தத்தை அனுபவிக்கிறது.

இந்த வகையின் முறிவு (தற்போதுள்ளவற்றுடன் பொது வரம்பு) அழைக்கப்படுகின்றன சரிசெய்யக்கூடிய இடைவெளி. ஏன் நீக்கக்கூடியது? ஏனெனில் செயல்பாடு முடியும் மறுவரையறைமுறிவு புள்ளியில்:

இது விசித்திரமாகத் தெரிகிறதா? இருக்கலாம். ஆனால் அத்தகைய செயல்பாடு குறிப்பீடு எதற்கும் முரணாக இல்லை! இப்போது இடைவெளி மூடப்பட்டு அனைவரும் மகிழ்ச்சியாக உள்ளனர்:

முறையான சரிபார்ப்பைச் செய்வோம்:

2) - ஒரு பொதுவான வரம்பு உள்ளது;
3)

இவ்வாறு, மூன்று நிபந்தனைகளும் பூர்த்தி செய்யப்படுகின்றன, மேலும் ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் தொடர்ச்சியின் வரையறையின்படி ஒரு கட்டத்தில் செயல்பாடு தொடர்ச்சியாக இருக்கும்.

இருப்பினும், மதன் வெறுப்பாளர்கள் செயல்பாட்டை மோசமான வழியில் வரையறுக்கலாம், எடுத்துக்காட்டாக :

முதல் இரண்டு தொடர்ச்சி நிலைமைகள் இங்கே திருப்திகரமாக இருப்பது சுவாரஸ்யமானது:
1) - செயல்பாடு ஒரு குறிப்பிட்ட புள்ளியில் வரையறுக்கப்படுகிறது;
2) - ஒரு பொதுவான வரம்பு உள்ளது.

ஆனால் மூன்றாவது எல்லை கடக்கப்படவில்லை: , அதாவது புள்ளியில் உள்ள செயல்பாட்டின் வரம்பு சமமாக இல்லைகொடுக்கப்பட்ட புள்ளியில் கொடுக்கப்பட்ட செயல்பாட்டின் மதிப்பு.

இதனால், ஒரு கட்டத்தில் செயல்பாடு இடைநிறுத்தப்படுகிறது.

இரண்டாவது, சோகமான வழக்கு அழைக்கப்படுகிறது முதல் வகையான முறிவு ஒரு குதிப்புடன். மேலும் சோகம் என்பது ஒருதலைப்பட்ச வரம்புகளால் தூண்டப்படுகிறது வரையறுக்கப்பட்ட மற்றும் வேறுபட்டது. பாடத்தின் இரண்டாவது வரைபடத்தில் ஒரு எடுத்துக்காட்டு காட்டப்பட்டுள்ளது. இத்தகைய இடைவெளி பொதுவாக ஏற்படுகிறது துண்டு துண்டாக வரையறுக்கப்பட்ட செயல்பாடுகள், இது ஏற்கனவே கட்டுரையில் குறிப்பிடப்பட்டுள்ளது வரைபட மாற்றங்கள் பற்றி.

துண்டு துண்டாக செயல்பாட்டைக் கவனியுங்கள் மற்றும் அதன் வரைபடத்தை முடிப்போம். ஒரு வரைபடத்தை எவ்வாறு உருவாக்குவது? மிகவும் எளிமையானது. ஒரு அரை இடைவெளியில் நாம் ஒரு பரவளையத்தின் ஒரு பகுதியை வரைகிறோம் ( பச்சை), இடைவெளியில் - ஒரு நேர் கோடு பிரிவு (சிவப்பு) மற்றும் அரை இடைவெளியில் - ஒரு நேர் கோடு ( நீலம்).

மேலும், சமத்துவமின்மை காரணமாக, மதிப்பு தீர்மானிக்கப்படுகிறது இருபடி செயல்பாடு(பச்சை புள்ளி), மற்றும் சமத்துவமின்மை காரணமாக, மதிப்பு தீர்மானிக்கப்படுகிறது நேரியல் செயல்பாடு(நீல புள்ளி):

மிகவும் கடினமான சூழ்நிலையில், வரைபடத்தின் ஒவ்வொரு பகுதியின் புள்ளி-மூலம்-புள்ளி கட்டுமானத்தை நீங்கள் நாட வேண்டும் (முதல் பார்க்கவும் செயல்பாடுகளின் வரைபடங்கள் பற்றிய பாடம்).

இப்போது நாம் புள்ளியில் மட்டுமே ஆர்வமாக இருப்போம். அதன் தொடர்ச்சியை ஆராய்வோம்:

2) ஒரு பக்க வரம்புகளை கணக்கிடுவோம்.

இடதுபுறத்தில் சிவப்பு கோடு பிரிவு உள்ளது, எனவே இடது பக்க வரம்பு:

வலதுபுறத்தில் நீல நேர் கோடு மற்றும் வலது புற வரம்பு:

இதன் விளைவாக, நாங்கள் பெற்றோம் வரையறுக்கப்பட்ட எண்கள், மற்றும் அவர்கள் சமமாக இல்லை. ஒருபக்க வரம்புகள் என்பதால் வரையறுக்கப்பட்ட மற்றும் வேறுபட்டது: , பின்னர் எங்கள் செயல்பாடு பொறுத்துக்கொள்ளும் ஒரு குதிப்புடன் முதல் வகையான இடைநிறுத்தம்.

இடைவெளியை அகற்ற முடியாது என்பது தர்க்கரீதியானது - முந்தைய எடுத்துக்காட்டில் இருந்ததைப் போல, செயல்பாட்டை மேலும் வரையறுக்க முடியாது மற்றும் "ஒன்றாக ஒட்டவும்" முடியாது.

இரண்டாவது வகையான தொடர்ச்சியற்ற புள்ளிகள்

பொதுவாக, மற்ற அனைத்து சிதைவு நிகழ்வுகளும் புத்திசாலித்தனமாக இந்த வகைக்குள் வகைப்படுத்தப்படுகின்றன. நான் எல்லாவற்றையும் பட்டியலிட மாட்டேன், ஏனென்றால் நடைமுறையில், 99% சிக்கல்களில் நீங்கள் சந்திப்பீர்கள் முடிவற்ற இடைவெளி- இடது கை அல்லது வலது கை, மற்றும் பெரும்பாலும், இரண்டு வரம்புகளும் எல்லையற்றவை.

மற்றும், நிச்சயமாக, மிகத் தெளிவான படம் பூஜ்ஜியத்தில் உள்ள ஹைபர்போலா ஆகும். இங்கே இரண்டு ஒருபக்க வரம்புகளும் எல்லையற்றவை: , எனவே, செயல்பாடு புள்ளியில் இரண்டாவது வகையான இடைநிறுத்தத்தை பாதிக்கிறது.

எனது கட்டுரைகளை முடிந்தவரை பலதரப்பட்ட உள்ளடக்கத்துடன் நிரப்ப முயற்சிக்கிறேன், எனவே இதுவரை பார்க்காத செயல்பாட்டின் வரைபடத்தைப் பார்ப்போம்:

நிலையான திட்டத்தின் படி:

1) வகுத்தல் பூஜ்ஜியத்திற்குச் செல்வதால் இந்த கட்டத்தில் செயல்பாடு வரையறுக்கப்படவில்லை.

நிச்சயமாக, செயல்பாட்டில் ஒரு இடைநிறுத்தம் ஏற்படுகிறது என்று நாம் உடனடியாக முடிவு செய்யலாம் , ஆனால் அடிக்கடி நிபந்தனைக்கு தேவைப்படும் இடைநிறுத்தத்தின் தன்மையை வகைப்படுத்துவது நல்லது. இதைச் செய்ய:

பதிவு செய்வதன் மூலம் நாங்கள் சொல்கிறோம் என்பதை உங்களுக்கு நினைவூட்டுகிறேன் எல்லையற்ற எதிர்மறை எண் , மற்றும் நுழைவின் கீழ் - எண்ணற்ற நேர்மறை எண்.

ஒரு பக்க வரம்புகள் எல்லையற்றவை, அதாவது செயல்பாடு புள்ளியில் 2வது வகையான இடைநிறுத்தத்தை அனுபவிக்கிறது. y-அச்சு என்பது செங்குத்து அறிகுறிவரைபடத்திற்கு.

இரண்டும் ஒரு பக்க வரம்புகள் இருப்பது அசாதாரணமானது அல்ல, ஆனால் அவற்றில் ஒன்று மட்டுமே எல்லையற்றது, எடுத்துக்காட்டாக:

இது செயல்பாட்டின் வரைபடம்.

தொடர்ச்சிக்கான புள்ளியை நாங்கள் ஆராய்வோம்:

1) இந்த கட்டத்தில் செயல்பாடு வரையறுக்கப்படவில்லை.

2) ஒரு பக்க வரம்புகளை கணக்கிடுவோம்:

விரிவுரையின் கடைசி இரண்டு எடுத்துக்காட்டுகளில் இதுபோன்ற ஒருதலைப்பட்ச வரம்புகளைக் கணக்கிடும் முறையைப் பற்றி பேசுவோம், இருப்பினும் பல வாசகர்கள் ஏற்கனவே எல்லாவற்றையும் பார்த்து யூகித்துள்ளனர்.

இடது கை வரம்பு வரையறுக்கப்பட்டுள்ளது மற்றும் பூஜ்ஜியத்திற்கு சமம் (நாம் "புள்ளிக்கு செல்ல மாட்டோம்"), ஆனால் வலது புற வரம்பு எல்லையற்றது மற்றும் வரைபடத்தின் ஆரஞ்சு கிளை அதன் எல்லைக்கு வரம்பற்றதாக நெருங்குகிறது. செங்குத்து அறிகுறி, சமன்பாடு மூலம் கொடுக்கப்பட்டது(கருப்பு புள்ளியிடப்பட்ட கோடு).

அதனால் செயல்பாடு பாதிக்கப்படுகிறது இரண்டாவது வகையான இடைநிறுத்தம்புள்ளியில்.

1 வது வகையான இடைநிறுத்தத்தைப் பொறுத்தவரை, செயல்பாட்டை நிறுத்தும் புள்ளியிலேயே வரையறுக்கலாம். எடுத்துக்காட்டாக, துண்டு துண்டான செயல்பாட்டிற்கு ஆயத்தொலைவுகளின் தோற்றத்தில் கருப்பு தடிமனான புள்ளியை வைக்க தயங்க வேண்டாம். வலதுபுறத்தில் ஒரு ஹைப்பர்போலாவின் கிளை உள்ளது, வலதுபுறம் எல்லையற்றது. இந்த வரைபடம் எப்படி இருக்கும் என்று கிட்டத்தட்ட அனைவருக்கும் ஒரு யோசனை இருப்பதாக நான் நினைக்கிறேன்.

அனைவரும் எதிர்பார்த்தது:

தொடர்ச்சிக்கான செயல்பாட்டை எவ்வாறு ஆராய்வது?

ஒரு கட்டத்தில் தொடர்ச்சிக்கான செயல்பாட்டின் ஆய்வு ஏற்கனவே நிறுவப்பட்ட வழக்கமான திட்டத்தின் படி மேற்கொள்ளப்படுகிறது, இது தொடர்ச்சியின் மூன்று நிபந்தனைகளை சரிபார்க்கிறது:

எடுத்துக்காட்டு 1

செயல்பாட்டை ஆராயுங்கள்

தீர்வு:

1) செயல்பாடு வரையறுக்கப்படாத ஒரே புள்ளி மட்டுமே நோக்கத்தில் உள்ளது.

2) ஒரு பக்க வரம்புகளை கணக்கிடுவோம்:

ஒரு பக்க வரம்புகள் வரையறுக்கப்பட்டவை மற்றும் சமமானவை.

இதனால், அந்த கட்டத்தில் செயல்பாடு நீக்கக்கூடிய இடைநிறுத்தத்தை அனுபவிக்கிறது.

இந்த செயல்பாட்டின் வரைபடம் எப்படி இருக்கும்?

நான் எளிமைப்படுத்த விரும்புகிறேன் , மற்றும் ஒரு சாதாரண பரவளையத்தைப் பெறுவது போல் தெரிகிறது. ஆனால்அசல் செயல்பாடு புள்ளியில் வரையறுக்கப்படவில்லை, எனவே பின்வரும் பிரிவு தேவைப்படுகிறது:

வரைபடத்தை உருவாக்குவோம்:

பதில்: செயல்பாடு நீக்கக்கூடிய இடைநிறுத்தத்தை அனுபவிக்கும் புள்ளியைத் தவிர முழு எண் கோட்டிலும் தொடர்ச்சியாக இருக்கும்.

செயல்பாடு ஒரு நல்ல அல்லது மிகவும் நல்ல வழியில் மேலும் வரையறுக்கப்படலாம், ஆனால் நிபந்தனையின் படி இது தேவையில்லை.

இது தொலைதூர உதாரணம் என்கிறீர்களா? இல்லவே இல்லை. இது நடைமுறையில் டஜன் கணக்கான முறை நடந்துள்ளது. தளத்தின் அனைத்து பணிகளும் உண்மையான சுயாதீன வேலை மற்றும் சோதனைகளிலிருந்து வந்தவை.

எங்களுக்கு பிடித்த தொகுதிகளை அகற்றுவோம்:

எடுத்துக்காட்டு 2

செயல்பாட்டை ஆராயுங்கள் தொடர்ச்சிக்காக. செயல்பாடு இடைநிறுத்தங்கள் இருந்தால், அவற்றின் தன்மையைத் தீர்மானிக்கவும். வரைபடத்தை இயக்கவும்.

தீர்வு: சில காரணங்களால், மாணவர்கள் பயப்படுகிறார்கள் மற்றும் ஒரு தொகுதியுடன் செயல்பாடுகளை விரும்புவதில்லை, இருப்பினும் அவற்றில் சிக்கலான எதுவும் இல்லை. பாடத்தில் இதுபோன்ற விஷயங்களை நாங்கள் ஏற்கனவே கொஞ்சம் தொட்டுள்ளோம். வரைபடங்களின் வடிவியல் மாற்றங்கள். தொகுதி எதிர்மறையாக இல்லாததால், இது பின்வருமாறு விரிவாக்கப்படுகிறது: , "ஆல்ஃபா" என்பது சில வெளிப்பாடு. இந்த வழக்கில், எங்கள் செயல்பாடு துண்டு துண்டாக எழுதப்பட வேண்டும்:

ஆனால் இரண்டு துண்டுகளின் பின்னங்களும் குறைக்கப்பட வேண்டும். குறைப்பு, முந்தைய எடுத்துக்காட்டில், விளைவுகள் இல்லாமல் நடக்காது. வகுத்தல் பூஜ்ஜியத்திற்குச் செல்வதால் அசல் செயல்பாடு புள்ளியில் வரையறுக்கப்படவில்லை. எனவே, கணினி கூடுதலாக நிபந்தனையை குறிப்பிட வேண்டும் , மற்றும் முதல் சமத்துவமின்மையை கடுமையாக்க வேண்டும்:

இப்போது மிகவும் பற்றி பயனுள்ள வரவேற்புதீர்வுகள்: வரைவில் பணியை முடிப்பதற்கு முன், ஒரு வரைபடத்தை உருவாக்குவது சாதகமானது (நிபந்தனைகள் தேவையா இல்லையா என்பதைப் பொருட்படுத்தாமல்). இது முதலாவதாக, தொடர்ச்சியின் புள்ளிகள் மற்றும் இடைநிறுத்தத்தின் புள்ளிகளை உடனடியாகக் காண உதவும், இரண்டாவதாக, ஒருதலைப்பட்ச வரம்புகளைக் கண்டறியும் போது 100% பிழைகளிலிருந்து உங்களைப் பாதுகாக்கும்.

வரைவோம். எங்கள் கணக்கீடுகளின்படி, புள்ளியின் இடதுபுறத்தில் ஒரு பரவளையத்தின் (நீல நிறம்) ஒரு பகுதியை வரைய வேண்டும், மற்றும் வலதுபுறம் - ஒரு பரவளையத்தின் ஒரு துண்டு (சிவப்பு நிறம்), செயல்பாடு வரையறுக்கப்படவில்லை தன்னை சுட்டிக்காட்டுகிறது:

சந்தேகம் இருந்தால், சில x மதிப்புகளை எடுத்து செயல்பாட்டில் செருகவும் (தொகுதி சாத்தியமான கழித்தல் அடையாளத்தை அழிக்கிறது என்பதை நினைவில் கொள்க) மற்றும் வரைபடத்தை சரிபார்க்கவும்.

தொடர்ச்சிக்கான செயல்பாட்டை பகுப்பாய்வு ரீதியாக ஆராய்வோம்:

1) செயல்பாடு புள்ளியில் வரையறுக்கப்படவில்லை, எனவே அது தொடர்ச்சியாக இல்லை என்று உடனடியாக சொல்லலாம்.

2) இடைநிறுத்தத்தின் தன்மையை நிறுவுவோம், ஒரு பக்க வரம்புகளை கணக்கிடுகிறோம்:

ஒருபக்க வரம்புகள் வரையறுக்கப்பட்டவை மற்றும் வேறுபட்டவை. வரம்புகளைக் கண்டறியும் போது, இடைவேளை புள்ளியில் செயல்பாடு வரையறுக்கப்பட்டதா இல்லையா என்பது முக்கியமில்லை என்பதை மீண்டும் கவனத்தில் கொள்ளவும்.

இப்போது எஞ்சியிருப்பது வரைவில் இருந்து வரைபடத்தை மாற்றுவது (இது ஆராய்ச்சியின் உதவியுடன் செய்யப்பட்டது ;-)) மற்றும் பணியை முடிக்க:

பதில்: ஒரு ஜம்ப் மூலம் முதல் வகையான இடைநிறுத்தத்தை அனுபவிக்கும் புள்ளியைத் தவிர முழு எண் கோட்டிலும் செயல்பாடு தொடர்கிறது.

சில சமயங்களில் அவர்களுக்கு இடைநிறுத்தம் தாவலின் கூடுதல் அறிகுறி தேவைப்படுகிறது. இது எளிமையாக கணக்கிடப்படுகிறது - வலது வரம்பிலிருந்து நீங்கள் இடது வரம்பை கழிக்க வேண்டும்: , அதாவது, இடைவேளையின் போது எங்கள் செயல்பாடு 2 அலகுகள் கீழே குதித்தது (கழித்தல் அடையாளம் நமக்குச் சொல்வது போல்).

எடுத்துக்காட்டு 3

செயல்பாட்டை ஆராயுங்கள் தொடர்ச்சிக்காக. செயல்பாடு இடைநிறுத்தங்கள் இருந்தால், அவற்றின் தன்மையைத் தீர்மானிக்கவும். ஒரு வரைதல் செய்யுங்கள்.

என்பதற்கு இது ஒரு உதாரணம் சுதந்திரமான முடிவு, பாடத்தின் முடிவில் மாதிரி தீர்வு.

செயல்பாடு மூன்று பகுதிகளைக் கொண்டிருக்கும் போது, பணியின் மிகவும் பிரபலமான மற்றும் பரவலான பதிப்பிற்கு செல்லலாம்:

எடுத்துக்காட்டு 4

தொடர்ச்சிக்கான ஒரு செயல்பாட்டை ஆராய்ந்து, செயல்பாட்டின் வரைபடத்தை வரையவும் .

தீர்வு: செயல்பாட்டின் மூன்று பகுதிகளும் தொடர்புடைய இடைவெளியில் தொடர்ச்சியாக இருக்கும் என்பது வெளிப்படையானது, எனவே துண்டுகளுக்கு இடையில் "சந்தி" இன் இரண்டு புள்ளிகளை மட்டுமே சரிபார்க்க வேண்டும். முதலில், ஒரு வரைவு வரைவோம்; ஒரே விஷயம் என்னவென்றால், நமது ஒருமைப் புள்ளிகளை நாம் கவனமாகப் பின்பற்ற வேண்டும்: சமத்துவமின்மை காரணமாக, மதிப்பு நேர் கோட்டிற்கு (பச்சை புள்ளி) சொந்தமானது, மற்றும் சமத்துவமின்மை காரணமாக, மதிப்பு பரவளையத்திற்கு (சிவப்பு புள்ளி) சொந்தமானது:

சரி, கொள்கையளவில், எல்லாம் தெளிவாக உள்ளது =) எஞ்சியிருப்பது முடிவை முறைப்படுத்துவதுதான். இரண்டு "கூட்டு" புள்ளிகளில் ஒவ்வொன்றிற்கும், நாங்கள் 3 தொடர்ச்சி நிலைகளை தரமாக சரிபார்க்கிறோம்:

நான்)தொடர்ச்சிக்கான புள்ளியை நாங்கள் ஆராய்வோம்

ஒருபக்க வரம்புகள் வரையறுக்கப்பட்டவை மற்றும் வேறுபட்டவை.

வலது மற்றும் இடது வரம்புகளுக்கு இடையே உள்ள வித்தியாசமாக இடைநிறுத்தம் தாவலை கணக்கிடுவோம்:
, அதாவது, வரைபடம் ஒரு யூனிட்டை உயர்த்தியது.

II)தொடர்ச்சிக்கான புள்ளியை நாங்கள் ஆராய்வோம்

1) - செயல்பாடு ஒரு குறிப்பிட்ட புள்ளியில் வரையறுக்கப்படுகிறது.

2) ஒரு பக்க வரம்புகளைக் கண்டறியவும்:

- ஒரு பக்க வரம்புகள் வரையறுக்கப்பட்டவை மற்றும் சமமானவை, அதாவது பொதுவான வரம்பு உள்ளது.

3) - ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வரம்பு ஒரு குறிப்பிட்ட புள்ளியில் இந்த செயல்பாட்டின் மதிப்புக்கு சமம்.

இறுதி கட்டத்தில், வரைபடத்தை இறுதி பதிப்பிற்கு மாற்றுகிறோம், அதன் பிறகு இறுதி நாண் வைக்கிறோம்:

பதில்: செயல்பாடு முழு எண் கோட்டிலும் தொடர்ச்சியாக இருக்கும், அது ஒரு ஜம்ப் மூலம் முதல் வகையான இடைநிறுத்தத்தை அனுபவிக்கும் புள்ளியைத் தவிர.

எடுத்துக்காட்டு 5

தொடர்ச்சிக்கான ஒரு செயல்பாட்டை ஆராய்ந்து அதன் வரைபடத்தை உருவாக்கவும் .

இது சுயாதீன தீர்வுக்கான ஒரு எடுத்துக்காட்டு, ஒரு குறுகிய தீர்வு மற்றும் பாடத்தின் முடிவில் சிக்கலின் தோராயமான மாதிரி.

ஒரு கட்டத்தில் செயல்பாடு தொடர்ச்சியாக இருக்க வேண்டும், மற்றொன்றில் இடைநிறுத்தம் இருக்க வேண்டும் என்ற எண்ணத்தை நீங்கள் பெறலாம். நடைமுறையில், இது எப்போதும் இல்லை. மீதமுள்ள எடுத்துக்காட்டுகளை புறக்கணிக்க வேண்டாம் - பல சுவாரஸ்யமான மற்றும் முக்கியமான அம்சங்கள் இருக்கும்:

எடுத்துக்காட்டு 6

ஒரு செயல்பாடு வழங்கப்பட்டது . புள்ளிகளில் தொடர்ச்சிக்கான செயல்பாட்டை ஆராயுங்கள். ஒரு வரைபடத்தை உருவாக்கவும்.

தீர்வு: மீண்டும் உடனடியாக வரைவில் வரைபடத்தை இயக்கவும்:

இந்த வரைபடத்தின் தனித்தன்மை என்னவென்றால், துண்டான செயல்பாடு abscissa அச்சின் சமன்பாட்டால் வழங்கப்படுகிறது. இந்தப் பகுதி இங்கு வரையப்பட்டுள்ளது பச்சை, மற்றும் ஒரு நோட்புக்கில் இது பொதுவாக தடிமனாக சிறப்பிக்கப்படுகிறது ஒரு எளிய பென்சிலுடன். மற்றும், நிச்சயமாக, எங்கள் ரேம்ஸ் பற்றி மறந்துவிடாதே: மதிப்பு தொடுகோடு கிளைக்கு (சிவப்பு புள்ளி) சொந்தமானது, மற்றும் மதிப்பு நேர் கோட்டிற்கு சொந்தமானது.

வரைபடத்திலிருந்து எல்லாம் தெளிவாக உள்ளது - செயல்பாடு முழு எண் கோட்டிலும் தொடர்கிறது, எஞ்சியிருப்பது தீர்வை முறைப்படுத்துவது மட்டுமே, இது 3-4 ஒத்த எடுத்துக்காட்டுகளுக்குப் பிறகு முழு ஆட்டோமேஷனுக்கு கொண்டு வரப்படுகிறது:

நான்)தொடர்ச்சிக்கான புள்ளியை நாங்கள் ஆராய்வோம்

1) - செயல்பாடு ஒரு குறிப்பிட்ட புள்ளியில் வரையறுக்கப்படுகிறது.

2) ஒரு பக்க வரம்புகளை கணக்கிடுவோம்:

, அதாவது பொதுவான வரம்பு உள்ளது.

ஒரு வேளை, ஒரு அற்பமான உண்மையை உங்களுக்கு நினைவூட்டுகிறேன்: மாறிலியின் வரம்பு மாறிலிக்கு சமம். இந்த வழக்கில், பூஜ்ஜியத்தின் வரம்பு பூஜ்ஜியத்திற்கு சமமாக இருக்கும் (இடது கை வரம்பு).

இவ்வாறு, ஒரு புள்ளியில் செயல்பாட்டின் தொடர்ச்சியின் வரையறையின்படி, ஒரு புள்ளியில் ஒரு செயல்பாடு தொடர்கிறது.

II)தொடர்ச்சிக்கான புள்ளியை நாங்கள் ஆராய்வோம்

1) - செயல்பாடு ஒரு குறிப்பிட்ட புள்ளியில் வரையறுக்கப்படுகிறது.

2) ஒரு பக்க வரம்புகளைக் கண்டறியவும்:

இங்கே - ஒன்றின் வரம்பு அலகுக்கு சமம்.

- ஒரு பொதுவான வரம்பு உள்ளது.

வழக்கம் போல், ஆராய்ச்சிக்குப் பிறகு, எங்கள் வரைபடத்தை இறுதி பதிப்பிற்கு மாற்றுவோம்.

பதில்: செயல்பாடு புள்ளிகளில் தொடர்ச்சியாக இருக்கும்.

இந்த நிலையில், தொடர்ச்சிக்கான முழு செயல்பாட்டையும் படிப்பது பற்றி எங்களிடம் எதுவும் கேட்கப்படவில்லை என்பதை நினைவில் கொள்ளவும், மேலும் இது சிறந்த கணித வடிவமாக கருதப்படுகிறது. துல்லியமான மற்றும் தெளிவானகேட்கப்பட்ட கேள்விக்கான பதில். மூலம், நிபந்தனைகள் நீங்கள் ஒரு வரைபடத்தை உருவாக்கத் தேவையில்லை என்றால், அதை உருவாக்காமல் இருக்க உங்களுக்கு முழு உரிமையும் உள்ளது (பின்னர் ஆசிரியர் இதைச் செய்யும்படி கட்டாயப்படுத்தலாம்).

அதை நீங்களே தீர்க்க ஒரு சிறிய கணித "நாக்கு ட்விஸ்டர்":

எடுத்துக்காட்டு 7

ஒரு செயல்பாடு வழங்கப்பட்டது . புள்ளிகளில் தொடர்ச்சிக்கான செயல்பாட்டை ஆராயுங்கள். முறிப்பு புள்ளிகள் ஏதேனும் இருந்தால் வகைப்படுத்தவும். வரைபடத்தை இயக்கவும்.

அனைத்து "சொற்களையும்" சரியாக "உச்சரிக்க" முயற்சிக்கவும் =) மேலும் வரைபடத்தை இன்னும் துல்லியமாக வரையவும், துல்லியம், அது எல்லா இடங்களிலும் மிதமிஞ்சியதாக இருக்காது;-)

நீங்கள் நினைவில் வைத்துள்ளபடி, வரைபடத்தை உடனடியாக ஒரு வரைவாக முடிக்க நான் பரிந்துரைத்தேன், ஆனால் அவ்வப்போது நீங்கள் வரைபடம் எப்படி இருக்கும் என்பதை உடனடியாக கண்டுபிடிக்க முடியாத உதாரணங்களை நீங்கள் காணலாம். எனவே, சில சந்தர்ப்பங்களில், முதலில் ஒருதலைப்பட்ச வரம்புகளைக் கண்டறிவது சாதகமானது, பின்னர் மட்டுமே, ஆய்வின் அடிப்படையில், கிளைகளை சித்தரிக்கவும். இறுதி இரண்டு எடுத்துக்காட்டுகளில், சில ஒருதலைப்பட்ச வரம்புகளைக் கணக்கிடுவதற்கான ஒரு நுட்பத்தையும் கற்றுக்கொள்வோம்:

எடுத்துக்காட்டு 8

தொடர்ச்சிக்கான செயல்பாட்டை ஆராய்ந்து அதன் திட்ட வரைபடத்தை உருவாக்கவும்.

தீர்வு: மோசமான புள்ளிகள் வெளிப்படையானவை: (அடுக்குவெட்டின் வகுப்பினை பூஜ்ஜியமாகக் குறைக்கிறது) மற்றும் (முழுப் பகுதியின் வகுப்பினை பூஜ்ஜியமாகக் குறைக்கிறது). இந்த செயல்பாட்டின் வரைபடம் எப்படி இருக்கும் என்பது தெளிவாக இல்லை, அதாவது முதலில் சில ஆராய்ச்சி செய்வது நல்லது.

இந்த பாடத்தில் ஒரு செயல்பாட்டின் தொடர்ச்சியை எவ்வாறு நிறுவுவது என்பதைக் கற்றுக்கொள்வோம். வரம்புகளைப் பயன்படுத்தி இதைச் செய்வோம், அதில் ஒரு பக்க - வலது மற்றும் இடது, அவை பயமாக இல்லை, அவை எழுதப்பட்டிருந்தாலும்.

ஆனால் ஒரு செயல்பாட்டின் தொடர்ச்சி என்றால் என்ன? நாம் ஒரு கண்டிப்பான வரையறையைப் பெறும் வரை, காகிதத்திலிருந்து பென்சிலைத் தூக்காமல் வரையக்கூடிய ஒரு கோட்டை கற்பனை செய்வது எளிது. அத்தகைய கோடு வரையப்பட்டால், அது தொடர்ச்சியாக இருக்கும். இந்த வரி ஒரு தொடர்ச்சியான செயல்பாட்டின் வரைபடம்.

வரைபட ரீதியாக, இந்த கட்டத்தில் அதன் வரைபடம் "உடைக்கவில்லை" என்றால், ஒரு செயல்பாடு ஒரு கட்டத்தில் தொடர்ந்து இருக்கும். அத்தகைய தொடர்ச்சியான செயல்பாட்டின் வரைபடம் கீழே உள்ள படத்தில் காட்டப்பட்டுள்ளது.

வரம்பு மூலம் ஒரு செயல்பாட்டின் தொடர்ச்சியைத் தீர்மானித்தல்.மூன்று நிபந்தனைகள் பூர்த்தி செய்யப்பட்டால், ஒரு கட்டத்தில் ஒரு செயல்பாடு தொடர்ச்சியாக இருக்கும்:

1. செயல்பாடு புள்ளியில் வரையறுக்கப்படுகிறது.

பட்டியலிடப்பட்ட நிபந்தனைகளில் ஏதேனும் ஒன்று பூர்த்தி செய்யப்படாவிட்டால், செயல்பாடு புள்ளியில் தொடர்ந்து இருக்காது. இந்த வழக்கில், செயல்பாடு ஒரு இடைநிறுத்தத்தை பாதிக்கிறது என்றும், வரைபடத்தில் குறுக்கிடப்பட்ட வரைபடத்தின் புள்ளிகள் செயல்பாட்டின் இடைநிறுத்தப் புள்ளிகள் என்று அழைக்கப்படுகின்றன என்றும் அவர்கள் கூறுகிறார்கள். x=2 என்ற புள்ளியில் இடைநிறுத்தத்தை அனுபவிக்கும் அத்தகைய செயல்பாட்டின் வரைபடம் கீழே உள்ள படத்தில் உள்ளது.

எடுத்துக்காட்டு 1.செயல்பாடு f(x) பின்வருமாறு வரையறுக்கப்படுகிறது:

இந்தச் செயல்பாடு அதன் கிளைகளின் ஒவ்வொரு எல்லைப் புள்ளிகளிலும், அதாவது புள்ளிகளில் தொடர்ச்சியாக இருக்கும் x = 0 , x = 1 , x = 3 ?

தீர்வு. ஒவ்வொரு எல்லைப் புள்ளியிலும் ஒரு செயல்பாட்டின் தொடர்ச்சிக்கான மூன்று நிபந்தனைகளையும் நாங்கள் சரிபார்க்கிறோம். முதல் நிபந்தனை பூர்த்தி செய்யப்பட்டது, எதிலிருந்து செயல்பாடு வரையறுக்கப்பட்டுள்ளதுஒவ்வொரு எல்லைப் புள்ளிகளிலும் செயல்பாட்டின் வரையறையிலிருந்து பின்பற்றப்படுகிறது. மீதமுள்ள இரண்டு நிபந்தனைகளை சரிபார்க்க இது உள்ளது.

புள்ளி x= 0 இந்த இடத்தில் இடது கை வரம்பைக் கண்டுபிடிப்போம்:

வலது கை வரம்பைக் கண்டுபிடிப்போம்:

xஇந்த புள்ளியை உள்ளடக்கிய செயல்பாட்டின் கிளைக்கு = 0 கண்டுபிடிக்க வேண்டும், அதாவது இரண்டாவது கிளை. நாங்கள் அவற்றைக் காண்கிறோம்:

நாம் பார்க்க முடியும் என, செயல்பாட்டின் வரம்பு மற்றும் புள்ளியில் செயல்பாட்டின் மதிப்பு x= 0 சமம். எனவே, செயல்பாடு புள்ளியில் தொடர்ந்து உள்ளது x = 0 .

புள்ளி x= 1 இந்த இடத்தில் இடது கை வரம்பைக் கண்டுபிடிப்போம்:

வலது கை வரம்பைக் கண்டுபிடிப்போம்:

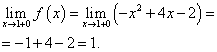
ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வரம்பு மற்றும் செயல்பாட்டின் மதிப்பு xஇந்த புள்ளியை உள்ளடக்கிய செயல்பாட்டின் கிளைக்கு = 1 கண்டுபிடிக்க வேண்டும், அதாவது இரண்டாவது கிளை. நாங்கள் அவற்றைக் காண்கிறோம்:

ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வரம்பு மற்றும் செயல்பாட்டின் மதிப்பு x= 1 சமம். எனவே, செயல்பாடு புள்ளியில் தொடர்ந்து உள்ளது x = 1 .

புள்ளி x= 3 இந்த இடத்தில் இடது கை வரம்பைக் கண்டுபிடிப்போம்:

வலது கை வரம்பைக் கண்டுபிடிப்போம்:

ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வரம்பு மற்றும் செயல்பாட்டின் மதிப்பு xஇந்த புள்ளியை உள்ளடக்கிய செயல்பாட்டின் கிளைக்கு = 3 கண்டுபிடிக்கப்பட வேண்டும், அதாவது இரண்டாவது கிளை. நாங்கள் அவற்றைக் காண்கிறோம்:

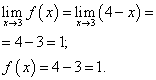ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வரம்பு மற்றும் செயல்பாட்டின் மதிப்பு x= 3 சமம். எனவே, செயல்பாடு புள்ளியில் தொடர்ந்து உள்ளது x = 3 .

முக்கிய முடிவு: இந்த செயல்பாடுஒவ்வொரு எல்லைப் புள்ளியிலும் தொடர்கிறது.

ஒரு கட்டத்தில் செயல்பாட்டின் தொடர்ச்சியை நீங்களே நிறுவுங்கள், பின்னர் தீர்வைப் பாருங்கள்

ஒரு செயல்பாட்டில் தொடர்ச்சியான மாற்றம் தாவல்கள் இல்லாமல் படிப்படியான மாற்றம் என வரையறுக்கப்படுகிறது, இதில் வாதத்தில் ஒரு சிறிய மாற்றம் செயல்பாட்டில் சிறிய மாற்றத்தை ஏற்படுத்துகிறது.

செயல்பாட்டில் இந்த தொடர்ச்சியான மாற்றத்தை ஒரு எடுத்துக்காட்டுடன் விளக்குவோம்.

மேசைக்கு மேலே ஒரு நூலில் ஒரு எடை தொங்கட்டும். இந்த சுமையின் செல்வாக்கின் கீழ், நூல் நீண்டுள்ளது, எனவே தூரம் எல்நூலின் இடைநீக்கப் புள்ளியில் இருந்து சுமை என்பது சுமையின் வெகுஜனத்தின் செயல்பாடாகும் மீ, அதாவது எல் = f(மீ) , மீ≥0 .

நீங்கள் சுமையின் வெகுஜனத்தை சற்று மாற்றினால், தூரம் எல்கொஞ்சம் மாறும்: சிறிய மாற்றங்கள் மீசிறிய மாற்றங்கள் ஒத்துப்போகின்றன எல். இருப்பினும், சுமையின் நிறை நூலின் இழுவிசை வலிமைக்கு அருகில் இருந்தால், சுமையின் வெகுஜனத்தில் சிறிது அதிகரிப்பு நூல் உடைந்து போகலாம்: தூரம் எல்திடீரென்று அதிகரிக்கும் மற்றும் இடைநீக்கம் புள்ளியில் இருந்து அட்டவணை மேற்பரப்புக்கு தூரத்திற்கு சமமாக மாறும். ஒரு செயல்பாட்டின் வரைபடம் எல் = f(மீ) படத்தில் காட்டப்பட்டுள்ளது. ஒரு பிரிவில், இந்த வரைபடம் ஒரு தொடர்ச்சியான (திடமான) வரியாகும், மேலும் ஒரு கட்டத்தில் அது குறுக்கிடப்படுகிறது. இதன் விளைவாக இரண்டு கிளைகளைக் கொண்ட ஒரு வரைபடம் உள்ளது. தவிர அனைத்து புள்ளிகளிலும், செயல்பாடு எல் = f(மீ) தொடர்ச்சியாக உள்ளது, ஆனால் ஒரு கட்டத்தில் அது ஒரு இடைநிறுத்தத்தைக் கொண்டுள்ளது.

தொடர்ச்சிக்கான ஒரு செயல்பாட்டைப் படிப்பது ஒரு சுயாதீனமான பணியாக இருக்கலாம் அல்லது செயல்பாட்டின் முழுமையான ஆய்வு மற்றும் அதன் வரைபடத்தை உருவாக்குவதற்கான நிலைகளில் ஒன்றாக இருக்கலாம்.

ஒரு இடைவெளியில் செயல்பாட்டின் தொடர்ச்சி

செயல்படட்டும் ஒய் = f(x) இடைவெளியில் வரையறுக்கப்பட்டுள்ளது] அ, பி[ மேலும் இந்த இடைவெளியின் ஒவ்வொரு புள்ளியிலும் தொடர்கிறது. பின்னர் அது இடைவெளியில் தொடர்ச்சியானது என்று அழைக்கப்படுகிறது] அ, பி[ . படிவத்தின் இடைவெளியில் ஒரு செயல்பாட்டின் தொடர்ச்சியின் கருத்து ]-∞ இதேபோல் வரையறுக்கப்படுகிறது, பி[ , ]அ, + ∞[ , ]- ∞, + ∞[ . இப்போது செயல்பாட்டை விடுங்கள் ஒய் = f(x) இடைவெளியில் வரையறுக்கப்பட்டது [ அ, பி] . ஒரு இடைவெளிக்கும் பிரிவுக்கும் உள்ள வேறுபாடு: இடைவெளியின் எல்லைப் புள்ளிகள் இடைவெளியில் சேர்க்கப்படவில்லை, ஆனால் ஒரு பிரிவின் எல்லைப் புள்ளிகள் பிரிவில் சேர்க்கப்பட்டுள்ளன. இங்கே நாம் ஒரு பக்க தொடர்ச்சி என்று அழைக்கப்படுவதைக் குறிப்பிட வேண்டும்: புள்ளியில் அ, பிரிவில் மீதமுள்ளது [ அ, பி] , நாம் வலதுபுறம் மற்றும் புள்ளியில் இருந்து மட்டுமே அணுக முடியும் பி- இடதுபுறம் மட்டுமே. செயல்பாடு இடைவெளியில் தொடர்ச்சியாக இருக்கும் [ அ, பி] , இந்தப் பிரிவின் அனைத்து உள் புள்ளிகளிலும் அது தொடர்ச்சியாக இருந்தால், புள்ளியில் வலதுபுறத்தில் தொடர்கிறது அமற்றும் புள்ளியில் தொடர்ந்து விடப்படுகிறது பி.

தொடர்ச்சியான செயல்பாட்டின் உதாரணம் எந்த அடிப்படை செயல்பாடுகளாக இருக்கலாம். ஒவ்வொன்றும் அடிப்படை செயல்பாடுஅது வரையறுக்கப்பட்ட எந்த இடைவெளியிலும் தொடர்கிறது. எடுத்துக்காட்டாக, செயல்பாடுகள் மற்றும் எந்த இடைவெளியிலும் தொடர்ச்சியாக இருக்கும் [ அ, பி], செயல்பாடு இடைவெளியில் தொடர்ந்து இருக்கும் [ 0 , பி] , ஒரு புள்ளியைக் கொண்டிருக்காத எந்தப் பிரிவிலும் செயல்பாடு தொடர்ச்சியாக இருக்கும் அ = 2 .

எடுத்துக்காட்டு 4.தொடர்ச்சிக்கான செயல்பாட்டை ஆராயுங்கள்.

தீர்வு. முதல் நிபந்தனையைப் பார்ப்போம். செயல்பாடு புள்ளிகளில் வரையறுக்கப்படவில்லை - 3 மற்றும் 3. முழு எண் கோட்டுடன் செயல்பாட்டின் தொடர்ச்சிக்கான நிபந்தனைகளில் குறைந்தபட்சம் ஒன்று திருப்தி அடையவில்லை. எனவே, இந்த செயல்பாடு இடைவெளியில் தொடர்ந்து இருக்கும்

எடுத்துக்காட்டு 5.அளவுருவின் மதிப்பை தீர்மானிக்கவும் அமுழுவதும் தொடர்ந்து வரையறையின் களம்செயல்பாடு

தீர்வு.

வலது புற வரம்பை இங்கே காணலாம்:

வெளிப்படையாக, புள்ளியில் மதிப்பு x= 2 சமமாக இருக்க வேண்டும் கோடாரி :

அ = 1,5 .

எடுத்துக்காட்டு 6.எந்த அளவுரு மதிப்புகளில் தீர்மானிக்கவும் அமற்றும் பிமுழுவதும் தொடர்ந்து வரையறையின் களம்செயல்பாடு

தீர்வு.
புள்ளியில் செயல்பாட்டின் இடது பக்க வரம்பைக் கண்டுபிடிப்போம்:

எனவே, புள்ளியில் உள்ள மதிப்பு 1 ஆக இருக்க வேண்டும்:

புள்ளியில் இடது கை செயல்பாட்டைக் கண்டுபிடிப்போம்:

வெளிப்படையாக, ஒரு கட்டத்தில் செயல்பாட்டின் மதிப்பு இதற்கு சமமாக இருக்க வேண்டும்:

பதில்: செயல்பாடு எப்போது என்பது வரையறையின் முழு களத்திலும் தொடர்ச்சியாக இருக்கும் அ = 1; பி = -3 .

தொடர்ச்சியான செயல்பாடுகளின் அடிப்படை பண்புகள்

கணிதம், முதலில், பல்வேறு இயக்க விதிகளைப் படிப்பதன் மூலம் தொடர்ச்சியான செயல்பாட்டின் கருத்துக்கு வந்தது. விண்வெளி மற்றும் நேரம் எல்லையற்றது, மற்றும் சார்பு, எடுத்துக்காட்டாக, பாதைகள் கள்அவ்வப்போது டி, சட்டத்தால் வெளிப்படுத்தப்பட்டது கள் = f(டி) , தொடர்ச்சியின் உதாரணம் தருகிறது செயல்பாடுகள் f(டி) . சூடான நீரின் வெப்பநிலையும் தொடர்ந்து மாறுகிறது; டி = f(டி) .

கணித பகுப்பாய்வில், தொடர்ச்சியான செயல்பாடுகளைக் கொண்ட சில பண்புகள் நிரூபிக்கப்பட்டுள்ளன. இந்த பண்புகளில் மிக முக்கியமானவற்றை முன்வைப்போம்.

1. ஒரு இடைவெளியில் தொடர்ச்சியான செயல்பாடு இடைவெளியின் முனைகளில் வெவ்வேறு குறிகளின் மதிப்புகளை எடுத்தால், இந்த இடைவெளியின் ஒரு கட்டத்தில் அது பூஜ்ஜியத்திற்கு சமமான மதிப்பை எடுக்கும். மிகவும் முறையான அறிக்கையில், இந்த சொத்து முதல் போல்சானோ-காச்சி தேற்றம் எனப்படும் தேற்றத்தில் கொடுக்கப்பட்டுள்ளது.

2. செயல்பாடு f(x), இடைவெளியில் தொடர்ந்து [ அ, பி] , அனைத்து இடைநிலை மதிப்புகளையும் இறுதி புள்ளிகளில் உள்ள மதிப்புகளுக்கு இடையில் எடுக்கும், அதாவது இடையில் f(அ) மற்றும் f(பி) . மிகவும் முறையான அறிக்கையில், இந்த சொத்து இரண்டாவது போல்சானோ-காச்சி தேற்றம் எனப்படும் தேற்றத்தில் கொடுக்கப்பட்டுள்ளது.