சீரற்ற மாறி எடுத்துக்காட்டுகளின் மாறுபாட்டைக் கண்டறிதல். ஒரு தனித்த சீரற்ற மாறியின் பரவல். நிலையான விலகல்
சிதறல் சீரற்ற மாறிஇந்த அளவின் மதிப்புகளின் பரவலின் அளவீடு ஆகும். குறைந்த மாறுபாடு என்பது மதிப்புகள் ஒன்றோடொன்று இணைந்திருப்பதைக் குறிக்கிறது. பெரிய சிதறல் மதிப்புகளின் வலுவான பரவலைக் குறிக்கிறது. ஒரு சீரற்ற மாறியின் மாறுபாடு என்ற கருத்து புள்ளிவிவரங்களில் பயன்படுத்தப்படுகிறது. எடுத்துக்காட்டாக, நீங்கள் இரண்டு மதிப்புகளின் மாறுபாட்டை ஒப்பிட்டுப் பார்த்தால் (ஆண் மற்றும் பெண் நோயாளிகளுக்கு இடையே), ஒரு மாறியின் முக்கியத்துவத்தை நீங்கள் சோதிக்கலாம். புள்ளிவிவர மாதிரிகளை உருவாக்கும்போது மாறுபாடு பயன்படுத்தப்படுகிறது, ஏனெனில் குறைந்த மாறுபாடு நீங்கள் மதிப்புகளை அதிகமாகப் பொருத்துகிறீர்கள் என்பதற்கான அறிகுறியாக இருக்கலாம்.படிகள்
மாதிரி மாறுபாட்டைக் கணக்கிடுகிறது
-
மாதிரி மதிப்புகளை பதிவு செய்யவும்.பெரும்பாலான சந்தர்ப்பங்களில், புள்ளிவிவர வல்லுநர்கள் குறிப்பிட்ட மக்கள்தொகையின் மாதிரிகளை மட்டுமே அணுக முடியும். எடுத்துக்காட்டாக, ஒரு விதியாக, புள்ளிவிவர வல்லுநர்கள் ரஷ்யாவில் உள்ள அனைத்து கார்களின் மக்கள்தொகையை பராமரிப்பதற்கான செலவை பகுப்பாய்வு செய்யவில்லை - அவர்கள் பல ஆயிரம் கார்களின் சீரற்ற மாதிரியை பகுப்பாய்வு செய்கிறார்கள். அத்தகைய மாதிரி ஒரு காரின் சராசரி விலையை தீர்மானிக்க உதவும், ஆனால், பெரும்பாலும், இதன் விளைவாக வரும் மதிப்பு உண்மையான ஒன்றிலிருந்து வெகு தொலைவில் இருக்கும்.
- எடுத்துக்காட்டாக, ஒரு ஓட்டலில் 6 நாட்களில் விற்கப்பட்ட பன்களின் எண்ணிக்கையை சீரற்ற வரிசையில் எடுத்துப் பார்ப்போம். மாதிரி உள்ளது அடுத்த பார்வை: 17, 15, 23, 7, 9, 13. இது மாதிரி, மக்கள் தொகை அல்ல, ஏனெனில் கஃபே திறந்திருக்கும் ஒவ்வொரு நாளும் விற்கப்படும் பன்கள் பற்றிய தரவு எங்களிடம் இல்லை.
- மதிப்புகளின் மாதிரியைக் காட்டிலும் மக்கள்தொகையைக் கொடுத்தால், அடுத்த பகுதிக்குத் தொடரவும்.
-
மாதிரி மாறுபாட்டைக் கணக்கிட ஒரு சூத்திரத்தை எழுதுங்கள்.சிதறல் என்பது ஒரு குறிப்பிட்ட அளவு மதிப்புகளின் பரவலின் அளவீடு ஆகும். மாறுபாடு மதிப்பு பூஜ்ஜியத்திற்கு எவ்வளவு நெருக்கமாக இருக்கிறதோ, அவ்வளவு நெருக்கமாக மதிப்புகள் ஒன்றாக தொகுக்கப்படுகின்றன. மதிப்புகளின் மாதிரியுடன் பணிபுரியும் போது, மாறுபாட்டைக் கணக்கிட பின்வரும் சூத்திரத்தைப் பயன்படுத்தவும்:
- s 2 (\டிஸ்ப்ளே ஸ்டைல் s^(2)) = ∑[(x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- எக்ஸ்) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))] / (n - 1)
- s 2 (\டிஸ்ப்ளே ஸ்டைல் s^(2))- இது சிதறல். சிதறல் சதுர அலகுகளில் அளவிடப்படுகிறது.
- x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- மாதிரியில் உள்ள ஒவ்வொரு மதிப்பும்.
- x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))நீங்கள் x̅ ஐ கழிக்க வேண்டும், அதை சதுரப்படுத்த வேண்டும், பின்னர் முடிவுகளை சேர்க்க வேண்டும்.
- x̅ - மாதிரி சராசரி (மாதிரி சராசரி).
- n - மாதிரியில் உள்ள மதிப்புகளின் எண்ணிக்கை.
-
மாதிரி சராசரியைக் கணக்கிடுங்கள்.இது x̅ எனக் குறிக்கப்படுகிறது. மாதிரி சராசரி ஒரு எளிய எண்கணித சராசரியாக கணக்கிடப்படுகிறது: மாதிரியில் உள்ள அனைத்து மதிப்புகளையும் சேர்த்து, பின்னர் மாதிரியில் உள்ள மதிப்புகளின் எண்ணிக்கையால் முடிவைப் பிரிக்கவும்.
- எங்கள் எடுத்துக்காட்டில், மாதிரியில் உள்ள மதிப்புகளைச் சேர்க்கவும்: 15 + 17 + 23 + 7 + 9 + 13 = 84
இப்போது மாதிரியில் உள்ள மதிப்புகளின் எண்ணிக்கையால் முடிவைப் பிரிக்கவும் (எங்கள் எடுத்துக்காட்டில் 6 உள்ளன): 84 ÷ 6 = 14.
மாதிரி சராசரி x̅ = 14. - மாதிரி சராசரி என்பது மாதிரியில் உள்ள மதிப்புகள் விநியோகிக்கப்படும் மைய மதிப்பாகும். மாதிரியைச் சுற்றியுள்ள மாதிரிக் கிளஸ்டரில் உள்ள மதிப்புகள் சராசரியாக இருந்தால், மாறுபாடு சிறியது; இல்லையெனில் மாறுபாடு பெரியது.
- எங்கள் எடுத்துக்காட்டில், மாதிரியில் உள்ள மதிப்புகளைச் சேர்க்கவும்: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
மாதிரியின் ஒவ்வொரு மதிப்பிலிருந்தும் மாதிரி சராசரியைக் கழிக்கவும்.இப்போது வித்தியாசத்தை கணக்கிடுங்கள் x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- x̅, எங்கே x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- மாதிரியில் உள்ள ஒவ்வொரு மதிப்பும். பெறப்பட்ட ஒவ்வொரு முடிவும் மாதிரி சராசரியிலிருந்து ஒரு குறிப்பிட்ட மதிப்பின் விலகலின் அளவைக் குறிக்கிறது, அதாவது, இந்த மதிப்பு மாதிரி சராசரியிலிருந்து எவ்வளவு தூரம் உள்ளது.
- எங்கள் எடுத்துக்காட்டில்:
x 1 (\டிஸ்ப்ளே ஸ்டைல் x_(1))- x̅ = 17 - 14 = 3
x 2 (\டிஸ்ப்ளே ஸ்டைல் x_(2))- x̅ = 15 - 14 = 1
x 3 (\டிஸ்ப்ளே ஸ்டைல் x_(3))- x = 23 - 14 = 9
x 4 (\டிஸ்ப்ளே ஸ்டைல் x_(4))- x̅ = 7 - 14 = -7
x 5 (\டிஸ்ப்ளே ஸ்டைல் x_(5))- x̅ = 9 - 14 = -5
x 6 (\டிஸ்ப்ளே ஸ்டைல் x_(6))- x̅ = 13 - 14 = -1 - பெறப்பட்ட முடிவுகளின் சரியான தன்மையை சரிபார்க்க எளிதானது, ஏனெனில் அவற்றின் கூட்டுத்தொகை பூஜ்ஜியத்திற்கு சமமாக இருக்க வேண்டும். இது சராசரி மதிப்பை நிர்ணயிப்பதோடு தொடர்புடையது எதிர்மறை மதிப்புகள்(சராசரி மதிப்பிலிருந்து சிறிய மதிப்புகளுக்கான தூரங்கள்) நேர்மறை மதிப்புகளால் முழுமையாக ஈடுசெய்யப்படுகின்றன (சராசரி மதிப்பிலிருந்து பெரிய மதிப்புகளுக்கான தூரங்கள்).
- எங்கள் எடுத்துக்காட்டில்:
-
மேலே குறிப்பிட்டுள்ளபடி, வேறுபாடுகளின் கூட்டுத்தொகை x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- x̅ பூஜ்ஜியத்திற்குச் சமமாக இருக்க வேண்டும். என்று அர்த்தம் சராசரி மாறுபாடுஎப்போதும் பூஜ்ஜியத்திற்கு சமமாக இருக்கும், இது ஒரு குறிப்பிட்ட அளவு மதிப்புகளின் பரவலைப் பற்றி எந்த யோசனையும் கொடுக்காது. இந்தச் சிக்கலைத் தீர்க்க, ஒவ்வொரு வித்தியாசத்தையும் சமப்படுத்தவும் x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- எக்ஸ். இது உங்களுக்கு மட்டுமே கிடைக்கும் நேர்மறை எண்கள், சேர்க்கும் போது 0 தராது.
- எங்கள் எடுத்துக்காட்டில்:
(x 1 (\டிஸ்ப்ளே ஸ்டைல் x_(1))- எக்ஸ்) 2 = 3 2 = 9 (\டிஸ்ப்ளே ஸ்டைல் ^(2)=3^(2)=9)
(x 2 (\டிஸ்ப்ளே ஸ்டைல் (x_(2))- எக்ஸ்) 2 = 1 2 = 1 (\டிஸ்ப்ளே ஸ்டைல் ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - வித்தியாசத்தின் சதுரத்தைக் கண்டுபிடித்தீர்கள் - x̅) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))மாதிரியில் உள்ள ஒவ்வொரு மதிப்புக்கும்.
- எங்கள் எடுத்துக்காட்டில்:
-
வேறுபாடுகளின் சதுரங்களின் கூட்டுத்தொகையைக் கணக்கிடுங்கள்.அதாவது, இப்படி எழுதப்பட்ட சூத்திரத்தின் பகுதியைக் கண்டறியவும்: ∑[( x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- எக்ஸ்) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))]. இங்கு Σ என்பது ஒவ்வொரு மதிப்பிற்கும் உள்ள வர்க்க வேறுபாடுகளின் கூட்டுத்தொகையைக் குறிக்கிறது x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))மாதிரியில். நீங்கள் ஏற்கனவே வர்க்க வேறுபாடுகளைக் கண்டறிந்துள்ளீர்கள் (x i (\டிஸ்ப்ளே ஸ்டைல் (x_(i)))- எக்ஸ்) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))ஒவ்வொரு மதிப்புக்கும் x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))மாதிரியில்; இப்போது இந்த சதுரங்களைச் சேர்க்கவும்.
- எங்கள் எடுத்துக்காட்டில்: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
முடிவை n - 1 ஆல் வகுக்கவும், n என்பது மாதிரியில் உள்ள மதிப்புகளின் எண்ணிக்கை.சில காலத்திற்கு முன்பு, மாதிரி மாறுபாட்டைக் கணக்கிட, புள்ளியியல் வல்லுநர்கள் முடிவை n ஆல் வகுத்தனர்; இந்த வழக்கில் நீங்கள் ஸ்கொயர் மாறுபாட்டின் சராசரியைப் பெறுவீர்கள், இது கொடுக்கப்பட்ட மாதிரியின் மாறுபாட்டை விவரிக்க சிறந்தது. ஆனால் எந்த மாதிரியும் ஒரு சிறிய பகுதி மட்டுமே என்பதை நினைவில் கொள்ளுங்கள் மக்கள் தொகைமதிப்புகள். நீங்கள் மற்றொரு மாதிரியை எடுத்து அதே கணக்கீடுகளைச் செய்தால், நீங்கள் வேறுபட்ட முடிவைப் பெறுவீர்கள். n - 1 ஆல் வகுத்தல் (வெறும் n ஐ விட) மக்கள்தொகை மாறுபாட்டின் மிகவும் துல்லியமான மதிப்பீட்டை வழங்குகிறது, இதில் நீங்கள் ஆர்வமாக உள்ளீர்கள். n - 1 ஆல் வகுத்தல் பொதுவானதாகிவிட்டது, எனவே இது மாதிரி மாறுபாட்டைக் கணக்கிடுவதற்கான சூத்திரத்தில் சேர்க்கப்பட்டுள்ளது.
- எங்கள் எடுத்துக்காட்டில், மாதிரியில் 6 மதிப்புகள் உள்ளன, அதாவது n = 6.
மாதிரி மாறுபாடு = s 2 = 166 6 − 1 = (\டிஸ்ப்ளே ஸ்டைல் s^(2)=(\frac (166)(6-1))=) 33,2
- எங்கள் எடுத்துக்காட்டில், மாதிரியில் 6 மதிப்புகள் உள்ளன, அதாவது n = 6.
-
மாறுபாடு மற்றும் நிலையான விலகல் இடையே உள்ள வேறுபாடு.சூத்திரத்தில் ஒரு அடுக்கு உள்ளது என்பதை நினைவில் கொள்ளவும், எனவே சிதறல் பகுப்பாய்வு செய்யப்படும் மதிப்பின் சதுர அலகுகளில் அளவிடப்படுகிறது. சில நேரங்களில் அத்தகைய அளவு செயல்படுவது மிகவும் கடினம்; அத்தகைய சந்தர்ப்பங்களில் அவர்கள் பயன்படுத்துகின்றனர் நிலையான விலகல், இது சமமானது சதுர வேர்சிதறலில் இருந்து. அதனால்தான் மாதிரி மாறுபாடு எனக் குறிக்கப்படுகிறது s 2 (\டிஸ்ப்ளே ஸ்டைல் s^(2)), மற்றும் மாதிரியின் நிலையான விலகல் பின்வருமாறு கள் (\டிஸ்ப்ளே ஸ்டைல்கள்).
- எங்கள் எடுத்துக்காட்டில், மாதிரியின் நிலையான விலகல்: s = √33.2 = 5.76.
மக்கள்தொகை மாறுபாட்டைக் கணக்கிடுதல்
-
சில மதிப்புகளின் தொகுப்பை பகுப்பாய்வு செய்யுங்கள்.பரிசீலனையில் உள்ள அளவின் அனைத்து மதிப்புகளும் தொகுப்பில் அடங்கும். உதாரணமாக, நீங்கள் குடியிருப்பாளர்களின் வயதைப் படிக்கிறீர்கள் என்றால் லெனின்கிராட் பகுதி, பின்னர் மக்கள் தொகையில் இந்த பகுதியில் வசிப்பவர்கள் அனைவரின் வயதும் அடங்கும். மக்கள்தொகையுடன் பணிபுரியும் போது, ஒரு அட்டவணையை உருவாக்கி அதில் மக்கள் தொகை மதிப்புகளை உள்ளிட பரிந்துரைக்கப்படுகிறது. பின்வரும் உதாரணத்தைக் கவனியுங்கள்:
- ஒரு குறிப்பிட்ட அறையில் 6 மீன்வளங்கள் உள்ளன. ஒவ்வொரு மீன்வளத்திலும் பின்வரும் எண்ணிக்கையிலான மீன்கள் உள்ளன:
x 1 = 5 (\டிஸ்ப்ளே ஸ்டைல் x_(1)=5)
x 2 = 5 (\டிஸ்ப்ளே ஸ்டைல் x_(2)=5)
x 3 = 8 (\டிஸ்ப்ளே ஸ்டைல் x_(3)=8)
x 4 = 12 (\டிஸ்ப்ளே ஸ்டைல் x_(4)=12)
x 5 = 15 (\டிஸ்ப்ளே ஸ்டைல் x_(5)=15)
x 6 = 18 (\டிஸ்ப்ளே ஸ்டைல் x_(6)=18)
- ஒரு குறிப்பிட்ட அறையில் 6 மீன்வளங்கள் உள்ளன. ஒவ்வொரு மீன்வளத்திலும் பின்வரும் எண்ணிக்கையிலான மீன்கள் உள்ளன:
-
மக்கள்தொகை மாறுபாட்டைக் கணக்கிடுவதற்கான சூத்திரத்தை எழுதுங்கள்.மக்கள்தொகையில் ஒரு குறிப்பிட்ட அளவின் அனைத்து மதிப்புகளும் உள்ளதால், கீழே உள்ள சூத்திரம் மக்கள்தொகை மாறுபாட்டின் சரியான மதிப்பைப் பெற உங்களை அனுமதிக்கிறது. மாதிரி மாறுபாட்டிலிருந்து மக்கள்தொகை மாறுபாட்டை வேறுபடுத்துவதற்கு (இது ஒரு மதிப்பீடு மட்டுமே), புள்ளியியல் வல்லுநர்கள் பல்வேறு மாறிகளைப் பயன்படுத்துகின்றனர்:
- σ 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)) = (∑(x i (\டிஸ்ப்ளே ஸ்டைல் x_(i)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)))/என்
- σ 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))- மக்கள்தொகை பரவல் ("சிக்மா ஸ்கொயர்" என படிக்கவும்). சிதறல் சதுர அலகுகளில் அளவிடப்படுகிறது.
- x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))- ஒவ்வொரு மதிப்பும் முழுமையாக.
- Σ - தொகை அடையாளம். அதாவது, ஒவ்வொரு மதிப்பிலிருந்தும் x i (\டிஸ்ப்ளே ஸ்டைல் x_(i))நீங்கள் μ ஐ கழித்து, அதை சதுரம் செய்து, பின்னர் முடிவுகளைச் சேர்க்க வேண்டும்.
- μ - மக்கள் தொகை சராசரி.
- n - மக்கள் தொகையில் உள்ள மதிப்புகளின் எண்ணிக்கை.
-
சராசரி மக்கள் தொகையைக் கணக்கிடுங்கள்.மக்கள்தொகையுடன் பணிபுரியும் போது, அதன் சராசரி μ (mu) எனக் குறிக்கப்படுகிறது. மக்கள்தொகை சராசரி ஒரு எளிய எண்கணித சராசரியாகக் கணக்கிடப்படுகிறது: மக்கள்தொகையில் உள்ள அனைத்து மதிப்புகளையும் சேர்த்து, பின்னர் மக்கள்தொகையில் உள்ள மதிப்புகளின் எண்ணிக்கையால் முடிவைப் பிரிக்கவும்.
- சராசரிகள் எப்போதும் எண்கணித சராசரியாக கணக்கிடப்படுவதில்லை என்பதை நினைவில் கொள்ளுங்கள்.
- எங்கள் எடுத்துக்காட்டில், மக்கள் தொகையின் அர்த்தம்: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\டிஸ்ப்ளே ஸ்டைல் (\frac (5+5+8+12+15+18)(6))) = 10,5
-
மக்கள்தொகையின் ஒவ்வொரு மதிப்பிலிருந்தும் மக்கள்தொகை சராசரியைக் கழிக்கவும்.வேறுபாடு மதிப்பு பூஜ்ஜியத்திற்கு நெருக்கமாக உள்ளது, குறிப்பிட்ட மதிப்பு மக்கள்தொகை சராசரிக்கு நெருக்கமாக உள்ளது. மக்கள்தொகையில் உள்ள ஒவ்வொரு மதிப்புக்கும் அதன் சராசரிக்கும் உள்ள வித்தியாசத்தைக் கண்டறியவும், மதிப்புகளின் விநியோகம் குறித்த முதல் யோசனையைப் பெறுவீர்கள்.
- எங்கள் எடுத்துக்காட்டில்:
x 1 (\டிஸ்ப்ளே ஸ்டைல் x_(1))- μ = 5 - 10.5 = -5.5
x 2 (\டிஸ்ப்ளே ஸ்டைல் x_(2))- μ = 5 - 10.5 = -5.5
x 3 (\டிஸ்ப்ளே ஸ்டைல் x_(3))- μ = 8 - 10.5 = -2.5
x 4 (\டிஸ்ப்ளே ஸ்டைல் x_(4))- μ = 12 - 10.5 = 1.5
x 5 (\டிஸ்ப்ளே ஸ்டைல் x_(5))- μ = 15 - 10.5 = 4.5
x 6 (\டிஸ்ப்ளே ஸ்டைல் x_(6))- μ = 18 - 10.5 = 7.5
- எங்கள் எடுத்துக்காட்டில்:
-
பெறப்பட்ட ஒவ்வொரு முடிவையும் சதுரம்.வேறுபாடு மதிப்புகள் நேர்மறை மற்றும் எதிர்மறை இரண்டும் இருக்கும்; இந்த மதிப்புகள் எண் கோட்டில் வரையப்பட்டால், அவை மக்கள்தொகை சராசரியின் வலது மற்றும் இடதுபுறத்தில் இருக்கும். இது நேர்மறை மற்றும் மாறுபாட்டைக் கணக்கிடுவதற்கு ஏற்றதல்ல எதிர்மறை எண்கள்ஒருவருக்கொருவர் ஈடுசெய்யுங்கள். எனவே பிரத்தியேகமாக நேர்மறை எண்களைப் பெற ஒவ்வொரு வித்தியாசத்தையும் சதுரப்படுத்தவும்.
- எங்கள் எடுத்துக்காட்டில்:
(x i (\டிஸ்ப்ளே ஸ்டைல் x_(i)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))ஒவ்வொரு மக்கள் தொகை மதிப்புக்கும் (i = 1 முதல் i = 6 வரை):
(-5,5)2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)) = 30,25
(-5,5)2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)), எங்கே x n (\டிஸ்ப்ளே ஸ்டைல் x_(n))- மக்கள் தொகையில் கடைசி மதிப்பு. - பெறப்பட்ட முடிவுகளின் சராசரி மதிப்பைக் கணக்கிட, நீங்கள் அவற்றின் தொகையைக் கண்டுபிடித்து அதை n ஆல் வகுக்க வேண்டும்:(( x 1 (\டிஸ்ப்ளே ஸ்டைல் x_(1)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)) + (x 2 (\டிஸ்ப்ளே ஸ்டைல் x_(2)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)) + ... + (x n (\டிஸ்ப்ளே ஸ்டைல் x_(n)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2)))/என்
- இப்போது மேலே உள்ள விளக்கத்தை மாறிகளைப் பயன்படுத்தி எழுதுவோம்: (∑( x i (\டிஸ்ப்ளே ஸ்டைல் x_(i)) - μ) 2 (\டிஸ்ப்ளே ஸ்டைல் ^(2))) / n மற்றும் மக்கள்தொகை மாறுபாட்டைக் கணக்கிடுவதற்கான சூத்திரத்தைப் பெறவும்.
- எங்கள் எடுத்துக்காட்டில்:
இதில் σ 2 j என்பது jth குழுவின் உள்குழு மாறுபாடு ஆகும்.
தொகுக்கப்படாத தரவுகளுக்கு எஞ்சிய மாறுபாடு- தோராயமான துல்லியத்தின் அளவீடு, அதாவது. அசல் தரவுக்கான பின்னடைவு வரியின் தோராயம்: 
y(t) என்பது போக்கு சமன்பாட்டைப் பயன்படுத்தும் முன்னறிவிப்பு; y t - ஆரம்ப இயக்கவியல் தொடர்; n - புள்ளிகளின் எண்ணிக்கை; p – பின்னடைவு சமன்பாடு குணகங்களின் எண்ணிக்கை (விளக்க மாறிகளின் எண்ணிக்கை).
இந்த எடுத்துக்காட்டில் இது அழைக்கப்படுகிறது பாரபட்சமற்ற மாறுபாடு மதிப்பீட்டாளர்.
எடுத்துக்காட்டு எண். 1. கட்டண வகைகளின்படி ஒரு சங்கத்தின் மூன்று நிறுவனங்களின் தொழிலாளர்களின் விநியோகம் பின்வரும் தரவுகளால் வகைப்படுத்தப்படுகிறது:
| கட்டண வகைதொழிலாளி | நிறுவனத்தில் உள்ள தொழிலாளர்களின் எண்ணிக்கை | ||
| நிறுவனம் 1 | நிறுவனம் 2 | நிறுவனம் 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
வரையறு:
1. ஒவ்வொரு நிறுவனத்திற்கும் மாறுபாடு (உள் குழு மாறுபாடுகள்);
2. குழுவிற்குள் உள்ள மாறுபாடுகளின் சராசரி;
3. இன்டர்குரூப் சிதறல்;
4. மொத்த மாறுபாடு.
தீர்வு.
சிக்கலைத் தீர்க்கத் தொடங்குவதற்கு முன், எந்த அம்சம் பயனுள்ளது மற்றும் எது காரணியானது என்பதைக் கண்டுபிடிப்பது அவசியம். பரிசீலனையில் உள்ள எடுத்துக்காட்டில், விளைவான பண்புக்கூறு “கட்டண வகை” மற்றும் காரணி பண்புக்கூறு “நிறுவனத்தின் எண் (பெயர்)” ஆகும்.
எங்களிடம் மூன்று குழுக்கள் (நிறுவனங்கள்) உள்ளன, அதற்காக குழு சராசரி மற்றும் உள்குழு மாறுபாடுகளைக் கணக்கிடுவது அவசியம்:

| நிறுவனம் | குழு சராசரி, | குழு மாறுபாட்டிற்குள், |
| 1 | 4 | 1,8 |
குழுவிற்குள் உள்ள மாறுபாடுகளின் சராசரி ( எஞ்சிய மாறுபாடு) சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படும்:
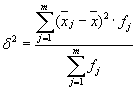
நீங்கள் எங்கே கணக்கிடலாம்:

அல்லது:

பிறகு:
மொத்த மாறுபாடு இதற்கு சமமாக இருக்கும்: s 2 = 1.6 + 0 = 1.6.
பின்வரும் இரண்டு சூத்திரங்களில் ஒன்றைப் பயன்படுத்தி மொத்த மாறுபாட்டையும் கணக்கிடலாம்:

நடைமுறைச் சிக்கல்களைத் தீர்க்கும் போது, இரண்டு மாற்று மதிப்புகளை மட்டுமே எடுக்கும் அம்சத்தை ஒருவர் அடிக்கடி கையாள வேண்டும். இந்த வழக்கில், நாங்கள் ஒரு அம்சத்தின் குறிப்பிட்ட மதிப்பின் எடையைப் பற்றி பேசவில்லை, ஆனால் மொத்தத்தில் அதன் பங்கைப் பற்றி பேசுகிறோம். ஆய்வு செய்யப்படும் பண்பைக் கொண்ட மக்கள்தொகை அலகுகளின் விகிதம் குறிக்கப்பட்டால் " ஆர்", மற்றும் இல்லாதவர்கள் - மூலம்" கே", பின்னர் சூத்திரத்தைப் பயன்படுத்தி மாறுபாட்டைக் கணக்கிடலாம்:
s 2 = p×q
எடுத்துக்காட்டு எண். 2. ஒரு குழுவில் உள்ள ஆறு தொழிலாளர்களின் உற்பத்தித் தரவுகளின் அடிப்படையில், இடைக்குழு மாறுபாட்டைத் தீர்மானித்து, மொத்த மாறுபாடு 12.2 ஆக இருந்தால், அவர்களின் தொழிலாளர் உற்பத்தித்திறனில் பணி மாற்றத்தின் தாக்கத்தை மதிப்பீடு செய்யவும்.
| குழு பணியாளர் எண். | தொழிலாளர் வெளியீடு, பிசிக்கள். | |
| முதல் ஷிப்டில் | இரண்டாவது ஷிப்டில் | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
தீர்வு. ஆரம்ப தரவு
| எக்ஸ் | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | மொத்தம் |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| மொத்தம் | 31 | 33 | 37 | 37 | 40 | 38 |
எங்களிடம் 6 குழுக்கள் உள்ளன, அதற்காக குழு சராசரி மற்றும் உள்குழு மாறுபாடுகளைக் கணக்கிடுவது அவசியம்.
1. ஒவ்வொரு குழுவின் சராசரி மதிப்புகளைக் கண்டறியவும்.
2. ஒவ்வொரு குழுவின் சராசரி சதுரத்தைக் கண்டறியவும்.
கணக்கீட்டு முடிவுகளை அட்டவணையில் சுருக்கமாகக் கூறுவோம்:
| குழு எண் | குழு சராசரி | குழுவிற்குள் மாறுபாடு |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. குழுவிற்குள் மாறுபாடுஒரு குழுவிற்குள் உள்ள அனைத்து காரணிகளின் செல்வாக்கின் கீழ் ஆய்வு செய்யப்பட்ட (விளைவான) பண்புகளின் மாற்றத்தை (மாறுபாடு) வகைப்படுத்துகிறது, குழுவாக்கத்தின் அடிப்படையான காரணியைத் தவிர:
சூத்திரத்தைப் பயன்படுத்தி உள்குழு மாறுபாடுகளின் சராசரியைக் கணக்கிடுகிறோம்:
4. இடைக்குழு மாறுபாடு குழுவின் அடிப்படையை உருவாக்கும் காரணி (காரணி பண்பு) செல்வாக்கின் கீழ் ஆய்வு செய்யப்பட்ட (விளைவு) பண்புகளின் மாற்றத்தை (மாறுபாடு) வகைப்படுத்துகிறது.
இடைக்குழு மாறுபாட்டை நாங்கள் பின்வருமாறு வரையறுக்கிறோம்:
எங்கே
பிறகு
மொத்த மாறுபாடுவிதிவிலக்கு இல்லாமல் அனைத்து காரணிகளின் (காரணி பண்புகள்) செல்வாக்கின் கீழ் ஆய்வு செய்யப்பட்ட (விளைவு) பண்புகளின் மாற்றத்தை (மாறுபாடு) வகைப்படுத்துகிறது. சிக்கலின் நிலைமைகளின்படி, இது 12.2 க்கு சமம்.
அனுபவ தொடர்பு உறவுமொத்த மாறுபாடு எவ்வளவு என்பதை அளவிடுகிறது விளைவாக அடையாளம்ஆய்வு செய்யப்பட்ட காரணியை ஏற்படுத்துகிறது. இது மொத்த மாறுபாட்டிற்கான காரணி மாறுபாட்டின் விகிதம்:
அனுபவ தொடர்பு உறவை நாங்கள் வரையறுக்கிறோம்:
குணாதிசயங்களுக்கிடையிலான இணைப்புகள் பலவீனமாகவும் வலுவாகவும் இருக்கலாம் (நெருக்கமானது). அவற்றின் அளவுகோல்கள் சாடாக் அளவில் மதிப்பிடப்படுகின்றன:
0.1 0.3 0.5 0.7 0.9 எங்கள் எடுத்துக்காட்டில், பண்பு Y மற்றும் காரணி X இடையே உள்ள உறவு பலவீனமாக உள்ளது
தீர்மான குணகம்.
தீர்மானத்தின் குணகத்தை தீர்மானிப்போம்:
எனவே, 0.67% மாறுபாடு குணாதிசயங்களுக்கிடையிலான வேறுபாடுகளால் ஏற்படுகிறது, மேலும் 99.37% மற்ற காரணிகளால் ஏற்படுகிறது.
முடிவுரை: இந்த வழக்கில், தொழிலாளர்களின் வெளியீடு ஒரு குறிப்பிட்ட ஷிப்டில் வேலை சார்ந்து இருக்காது, அதாவது. அவர்களின் தொழிலாளர் உற்பத்தித்திறனில் பணி மாற்றத்தின் தாக்கம் குறிப்பிடத்தக்கதாக இல்லை மற்றும் பிற காரணிகளால் ஏற்படுகிறது.
எடுத்துக்காட்டு எண். 3. சராசரி அடிப்படையில் ஊதியங்கள்மற்றும் இரண்டு குழுக்களின் தொழிலாளர்களுக்கு அதன் மதிப்பிலிருந்து ஸ்கொயர்டு விலகல்கள், மாறுபாடுகளைச் சேர்க்கும் விதியைப் பயன்படுத்துவதன் மூலம் மொத்த மாறுபாட்டைக் கண்டறியவும்:
தீர்வு:குழுவிற்குள் உள்ள மாறுபாடுகளின் சராசரி
இடைக்குழு மாறுபாட்டை நாங்கள் பின்வருமாறு வரையறுக்கிறோம்:
மொத்த மாறுபாடு: 480 + 13824 = 14304
எதிர்பார்ப்பு மற்றும் மாறுபாடு ஆகியவை சீரற்ற மாறியின் மிகவும் பொதுவாகப் பயன்படுத்தப்படும் எண் பண்புகளாகும். அவை விநியோகத்தின் மிக முக்கியமான அம்சங்களை வகைப்படுத்துகின்றன: அதன் நிலை மற்றும் சிதறலின் அளவு. பல நடைமுறைச் சிக்கல்களில், ஒரு சீரற்ற மாறியின் முழுமையான, முழுமையான பண்பு - விநியோகச் சட்டம் - ஒன்றைப் பெற முடியாது, அல்லது தேவையே இல்லை. இந்த சந்தர்ப்பங்களில், எண் பண்புகளைப் பயன்படுத்தி ஒரு சீரற்ற மாறியின் தோராயமான விளக்கத்திற்கு வரம்பிடப்பட்டுள்ளது.
எதிர்பார்க்கப்படும் மதிப்பு பெரும்பாலும் சீரற்ற மாறியின் சராசரி மதிப்பு என்று அழைக்கப்படுகிறது. ஒரு சீரற்ற மாறியின் பரவல் என்பது சிதறலின் சிறப்பியல்பு ஆகும், அதன் கணித எதிர்பார்ப்பைச் சுற்றி ஒரு சீரற்ற மாறி பரவுகிறது.
தனித்த சீரற்ற மாறியின் எதிர்பார்ப்பு
தனித்த சீரற்ற மாறியின் விநியோகத்தின் இயந்திர விளக்கத்தின் அடிப்படையில் முதலில் கணித எதிர்பார்ப்பு என்ற கருத்தை அணுகுவோம். x அச்சின் புள்ளிகளுக்கு இடையே அலகு நிறை விநியோகிக்கப்படட்டும் எக்ஸ்1 , எக்ஸ் 2 , ..., எக்ஸ் n, மற்றும் ஒவ்வொரு பொருள் புள்ளியும் தொடர்புடைய நிறை கொண்டது ப1 , ப 2 , ..., ப n. முழு அமைப்பின் நிலையை வகைப்படுத்தும் அப்சிஸ்ஸா அச்சில் ஒரு புள்ளியைத் தேர்ந்தெடுப்பது அவசியம் பொருள் புள்ளிகள், அவர்களின் வெகுஜனங்களை கணக்கில் எடுத்துக்கொள்வது. பொருள் புள்ளிகளின் அமைப்பின் நிறை மையத்தை அத்தகைய புள்ளியாகக் கொள்வது இயற்கையானது. இது சீரற்ற மாறியின் எடையுள்ள சராசரி எக்ஸ், ஒவ்வொரு புள்ளியின் abscissa எக்ஸ்நான்தொடர்புடைய நிகழ்தகவுக்கு சமமான "எடை" உடன் நுழைகிறது. இந்த வழியில் பெறப்பட்ட சீரற்ற மாறியின் சராசரி மதிப்பு எக்ஸ்அதன் கணித எதிர்பார்ப்பு என்று அழைக்கப்படுகிறது.
தனித்த சீரற்ற மாறியின் கணித எதிர்பார்ப்பு என்பது அதன் அனைத்து சாத்தியமான மதிப்புகளின் தயாரிப்புகளின் கூட்டுத்தொகை மற்றும் இந்த மதிப்புகளின் நிகழ்தகவுகள் ஆகும்:

எடுத்துக்காட்டு 1.வெற்றி-வெற்றி லாட்டரி ஏற்பாடு செய்யப்பட்டுள்ளது. 1000 வெற்றிகள் உள்ளன, அவற்றில் 400 10 ரூபிள் ஆகும். ஒவ்வொன்றும் 300-20 ரூபிள். ஒவ்வொன்றும் 200-100 ரூபிள். மற்றும் 100 - 200 ரூபிள் ஒவ்வொன்றும். என்ன சராசரி அளவுஒரு டிக்கெட் வாங்கியவர்களுக்கு வெற்றி?
தீர்வு. சராசரி வெற்றிகள் 10*400 + 20*300 + 100*200 + 200*100 = 50,000 ரூபிள்களுக்கு சமமான வெற்றிகளின் மொத்தத் தொகை 1000 (வெற்றிகளின் மொத்த அளவு) ஆல் வகுக்கப்பட்டுள்ளதா என்பதைக் கண்டுபிடிப்போம். பின்னர் நாம் 50000/1000 = 50 ரூபிள் கிடைக்கும். ஆனால் சராசரி வெற்றிகளைக் கணக்கிடுவதற்கான வெளிப்பாடு பின்வரும் வடிவத்தில் வழங்கப்படலாம்:

மறுபுறம், இந்த நிலைமைகளில், வென்ற தொகை ஒரு சீரற்ற மாறி ஆகும், இது 10, 20, 100 மற்றும் 200 ரூபிள் மதிப்புகளை எடுக்கலாம். முறையே 0.4 க்கு சமமான நிகழ்தகவுகளுடன்; 0.3; 0.2; 0.1 எனவே, எதிர்பார்க்கப்படும் சராசரி வெற்றியானது, வெற்றிகளின் அளவு மற்றும் அவற்றைப் பெறுவதற்கான நிகழ்தகவு ஆகியவற்றின் தயாரிப்புகளின் கூட்டுத்தொகைக்கு சமம்.
எடுத்துக்காட்டு 2.பதிப்பாளர் புதிய புத்தகத்தை வெளியிட முடிவு செய்தார். அவர் புத்தகத்தை 280 ரூபிள்களுக்கு விற்க திட்டமிட்டுள்ளார், அதில் அவர் 200, 50 - புத்தகக் கடை மற்றும் 30 - ஆசிரியரைப் பெறுவார். ஒரு புத்தகத்தை வெளியிடுவதற்கான செலவுகள் மற்றும் புத்தகத்தின் குறிப்பிட்ட எண்ணிக்கையிலான பிரதிகள் விற்கப்படுவதற்கான நிகழ்தகவு பற்றிய தகவல்களை அட்டவணை வழங்குகிறது.
வெளியீட்டாளர் எதிர்பார்க்கும் லாபத்தைக் கண்டறியவும்.
தீர்வு. சீரற்ற மாறி "லாபம்" என்பது விற்பனையிலிருந்து வரும் வருமானத்திற்கும் செலவுகளின் விலைக்கும் உள்ள வித்தியாசத்திற்கு சமம். உதாரணமாக, ஒரு புத்தகத்தின் 500 பிரதிகள் விற்கப்பட்டால், விற்பனையின் வருமானம் 200 * 500 = 100,000, மற்றும் வெளியீட்டு செலவு 225,000 ரூபிள் ஆகும். இதனால், வெளியீட்டாளர் 125,000 ரூபிள் இழப்பை எதிர்கொள்கிறார். பின்வரும் அட்டவணை சீரற்ற மாறியின் எதிர்பார்க்கப்படும் மதிப்புகளை சுருக்கமாகக் கூறுகிறது - லாபம்:
| எண் | லாபம் எக்ஸ்நான் | நிகழ்தகவு பநான் | எக்ஸ்நான் பநான் |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| மொத்தம்: | 1,00 | 25000 |
இவ்வாறு, நாம் பெறுகிறோம் எதிர்பார்க்கப்படும் மதிப்புவெளியீட்டாளரின் லாபம்:
![]() .
.
எடுத்துக்காட்டு 3.ஒரு ஷாட்டில் அடிக்கும் நிகழ்தகவு ப= 0.2. 5 க்கு சமமான வெற்றிகளின் எண்ணிக்கையின் கணித எதிர்பார்ப்பை வழங்கும் எறிபொருள்களின் நுகர்வு தீர்மானிக்கவும்.
தீர்வு. நாம் இதுவரை பயன்படுத்திய அதே கணித எதிர்பார்ப்பு சூத்திரத்திலிருந்து, நாங்கள் வெளிப்படுத்துகிறோம் எக்ஸ்- ஷெல் நுகர்வு:
![]() .
.
எடுத்துக்காட்டு 4.ஒரு சீரற்ற மாறியின் கணித எதிர்பார்ப்பைத் தீர்மானிக்கவும் எக்ஸ்மூன்று ஷாட்களுடன் கூடிய வெற்றிகளின் எண்ணிக்கை, ஒவ்வொரு ஷாட்டிலும் ஒரு வெற்றியின் நிகழ்தகவு ப = 0,4 .
குறிப்பு: சீரற்ற மாறி மதிப்புகளின் நிகழ்தகவைக் கண்டறியவும் பெர்னோலியின் சூத்திரம் .
கணித எதிர்பார்ப்பின் பண்புகள்
கணித எதிர்பார்ப்பின் பண்புகளை கருத்தில் கொள்வோம்.
சொத்து 1.ஒரு நிலையான மதிப்பின் கணித எதிர்பார்ப்பு இந்த மாறிலிக்கு சமம்:
சொத்து 2.நிலையான காரணியை கணித எதிர்பார்ப்பு அடையாளத்திலிருந்து எடுக்கலாம்:
![]()
சொத்து 3.சீரற்ற மாறிகளின் கூட்டுத்தொகையின் (வேறுபாடு) கணித எதிர்பார்ப்பு அவற்றின் கணித எதிர்பார்ப்புகளின் கூட்டுத்தொகைக்கு (வேறுபாடு) சமம்:
சொத்து 4.சீரற்ற மாறிகளின் ஒரு பொருளின் கணித எதிர்பார்ப்பு அவற்றின் கணித எதிர்பார்ப்புகளின் விளைபொருளுக்கு சமம்:
சொத்து 5.ஒரு சீரற்ற மாறியின் அனைத்து மதிப்புகளும் இருந்தால் எக்ஸ்அதே எண்ணிக்கையில் குறைதல் (அதிகரிப்பு). உடன், அதன் கணித எதிர்பார்ப்பு அதே எண்ணிக்கையில் குறையும் (அதிகரிக்கும்):
![]()
கணித எதிர்பார்ப்புக்கு மட்டுமே உங்களை கட்டுப்படுத்த முடியாது
பெரும்பாலான சந்தர்ப்பங்களில், கணித எதிர்பார்ப்பு மட்டுமே ஒரு சீரற்ற மாறியை போதுமான அளவு வகைப்படுத்த முடியாது.
சீரற்ற மாறிகளை விடுங்கள் எக்ஸ்மற்றும் ஒய்பின்வரும் விநியோகச் சட்டங்களால் வழங்கப்படுகின்றன:
| பொருள் எக்ஸ் | நிகழ்தகவு |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| பொருள் ஒய் | நிகழ்தகவு |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
இந்த அளவுகளின் கணித எதிர்பார்ப்புகள் ஒரே மாதிரியானவை - பூஜ்ஜியத்திற்கு சமம்:


இருப்பினும், அவற்றின் விநியோக முறை வேறுபட்டது. சீரற்ற மதிப்பு எக்ஸ்கணித எதிர்பார்ப்பு மற்றும் சீரற்ற மாறி ஆகியவற்றிலிருந்து சிறிது வேறுபடும் மதிப்புகளை மட்டுமே எடுக்க முடியும் ஒய்கணித எதிர்பார்ப்பில் இருந்து கணிசமாக விலகும் மதிப்புகளை எடுக்க முடியும். இதேபோன்ற உதாரணம்: சராசரி ஊதியம் அதிக மற்றும் குறைந்த ஊதியம் பெறும் தொழிலாளர்களின் பங்கை தீர்மானிக்க முடியாது. வேறு வார்த்தைகளில் கூறுவதானால், குறைந்தபட்சம் சராசரியாக அதிலிருந்து என்ன விலகல்கள் சாத்தியமாகும் என்பதை கணித எதிர்பார்ப்பிலிருந்து ஒருவர் தீர்மானிக்க முடியாது. இதைச் செய்ய, சீரற்ற மாறியின் மாறுபாட்டை நீங்கள் கண்டுபிடிக்க வேண்டும்.
தனித்த சீரற்ற மாறியின் மாறுபாடு
மாறுபாடுதனித்த சீரற்ற மாறி எக்ஸ்கணித எதிர்பார்ப்பிலிருந்து அதன் விலகலின் சதுரத்தின் கணித எதிர்பார்ப்பு என்று அழைக்கப்படுகிறது:

சீரற்ற மாறியின் நிலையான விலகல் எக்ஸ்அழைக்கப்பட்டது எண்கணித மதிப்புஅதன் மாறுபாட்டின் வர்க்கமூலம்:
![]() .
.
எடுத்துக்காட்டு 5.சீரற்ற மாறிகளின் மாறுபாடுகள் மற்றும் நிலையான விலகல்களைக் கணக்கிடுங்கள் எக்ஸ்மற்றும் ஒய், விநியோகச் சட்டங்கள் மேலே உள்ள அட்டவணையில் கொடுக்கப்பட்டுள்ளன.
தீர்வு. சீரற்ற மாறிகளின் கணித எதிர்பார்ப்புகள் எக்ஸ்மற்றும் ஒய், மேலே காணப்படும், பூஜ்ஜியத்திற்கு சமம். இல் சிதறல் சூத்திரத்தின் படி ஈ(எக்ஸ்)=ஈ(ஒய்)=0 நாம் பெறுகிறோம்:


பின்னர் சீரற்ற மாறிகளின் நிலையான விலகல்கள் எக்ஸ்மற்றும் ஒய்ஒப்பனை
![]() .
.
எனவே, அதே கணித எதிர்பார்ப்புகளுடன், சீரற்ற மாறியின் மாறுபாடு எக்ஸ்மிகவும் சிறியது, ஆனால் ஒரு சீரற்ற மாறி ஒய்- குறிப்பிடத்தக்கது. இது அவற்றின் விநியோகத்தில் உள்ள வேறுபாடுகளின் விளைவாகும்.
எடுத்துக்காட்டு 6.முதலீட்டாளருக்கு 4 மாற்று முதலீட்டு திட்டங்கள் உள்ளன. இந்தத் திட்டங்களில் எதிர்பார்க்கப்படும் லாபத்தை தொடர்புடைய நிகழ்தகவுடன் அட்டவணை சுருக்கமாகக் கூறுகிறது.
| திட்டம் 1 | திட்டம் 2 | திட்டம் 3 | திட்டம் 4 |
| 500, பி=1 | 1000, பி=0,5 | 500, பி=0,5 | 500, பி=0,5 |
| 0, பி=0,5 | 1000, பி=0,25 | 10500, பி=0,25 | |
| 0, பி=0,25 | 9500, பி=0,25 |
ஒவ்வொரு மாற்றுக்கும் கணித எதிர்பார்ப்பு, மாறுபாடு மற்றும் நிலையான விலகல் ஆகியவற்றைக் கண்டறியவும்.
தீர்வு. 3வது மாற்றுக்கு இந்த மதிப்புகள் எவ்வாறு கணக்கிடப்படுகின்றன என்பதைக் காண்பிப்போம்:
அட்டவணை அனைத்து மாற்றுகளுக்கும் காணப்படும் மதிப்புகளை சுருக்கமாகக் கூறுகிறது.
அனைத்து மாற்றுகளும் ஒரே கணித எதிர்பார்ப்புகளைக் கொண்டுள்ளன. இதன் பொருள் நீண்ட காலத்திற்கு அனைவருக்கும் ஒரே மாதிரியான வருமானம் உள்ளது. நிலையான விலகல் அபாயத்தின் அளவீடாக விளக்கப்படலாம் - அது அதிகமாக இருந்தால், முதலீட்டின் ஆபத்து அதிகமாகும். அதிக ஆபத்தை விரும்பாத முதலீட்டாளர் திட்டம் 1ஐத் தேர்ந்தெடுப்பார், ஏனெனில் அது மிகச்சிறிய நிலையான விலகலைக் கொண்டுள்ளது (0). முதலீட்டாளர் குறுகிய காலத்தில் ஆபத்து மற்றும் அதிக வருமானத்தை விரும்பினால், அவர் மிகப்பெரிய நிலையான விலகலுடன் திட்டத்தைத் தேர்ந்தெடுப்பார் - திட்டம் 4.
சிதறல் பண்புகள்
சிதறலின் பண்புகளை முன்வைப்போம்.
சொத்து 1.நிலையான மதிப்பின் மாறுபாடு பூஜ்ஜியமாகும்:
சொத்து 2.நிலையான காரணியை ஸ்கொயர் செய்வதன் மூலம் சிதறல் அடையாளத்திலிருந்து வெளியே எடுக்கலாம்:
![]() .
.
சொத்து 3.ஒரு சீரற்ற மாறியின் மாறுபாடு, இந்த மதிப்பின் சதுரத்தின் கணித எதிர்பார்ப்புக்கு சமம், இதிலிருந்து மதிப்பின் கணித எதிர்பார்ப்பின் வர்க்கம் கழிக்கப்படுகிறது:
![]() ,
,
எங்கே ![]() .
.
சொத்து 4.சீரற்ற மாறிகளின் கூட்டுத்தொகை (வேறுபாடு) மாறுபாடு அவற்றின் மாறுபாடுகளின் கூட்டுத்தொகைக்கு (வேறுபாடு) சமம்:
எடுத்துக்காட்டு 7.ஒரு தனித்த சீரற்ற மாறி என்று அறியப்படுகிறது எக்ஸ்இரண்டு மதிப்புகளை மட்டுமே எடுக்கும்: −3 மற்றும் 7. கூடுதலாக, கணித எதிர்பார்ப்பு அறியப்படுகிறது: ஈ(எக்ஸ்) = 4 . தனித்த சீரற்ற மாறியின் மாறுபாட்டைக் கண்டறியவும்.
தீர்வு. மூலம் குறிப்போம் பஒரு சீரற்ற மாறி ஒரு மதிப்பை எடுக்கும் நிகழ்தகவு எக்ஸ்1 = −3 . பின்னர் மதிப்பின் நிகழ்தகவு எக்ஸ்2 = 7 1 - ஆக இருக்கும் ப. கணித எதிர்பார்ப்புக்கான சமன்பாட்டைப் பெறுவோம்:
ஈ(எக்ஸ்) = எக்ஸ் 1 ப + எக்ஸ் 2 (1 − ப) = −3ப + 7(1 − ப) = 4 ,
நிகழ்தகவுகளை நாம் எங்கே பெறுகிறோம்: ப= 0.3 மற்றும் 1 - ப = 0,7 .
சீரற்ற மாறியின் விநியோக விதி:
| எக்ஸ் | −3 | 7 |
| ப | 0,3 | 0,7 |
இந்த ரேண்டம் மாறியின் மாறுபாட்டை, சிதறலின் பண்பு 3ல் இருந்து சூத்திரத்தைப் பயன்படுத்தி கணக்கிடுகிறோம்:
டி(எக்ஸ்) = 2,7 + 34,3 − 16 = 21 .
ஒரு சீரற்ற மாறியின் கணித எதிர்பார்ப்பை நீங்களே கண்டுபிடித்து, பின்னர் தீர்வைப் பாருங்கள்
எடுத்துக்காட்டு 8.தனித்த சீரற்ற மாறி எக்ஸ்இரண்டு மதிப்புகளை மட்டுமே எடுக்கிறது. இது நிகழ்தகவு 0.4 உடன் அதிக மதிப்புகள் 3 ஐ ஏற்றுக்கொள்கிறது. கூடுதலாக, சீரற்ற மாறியின் மாறுபாடு அறியப்படுகிறது டி(எக்ஸ்) = 6 . சீரற்ற மாறியின் கணித எதிர்பார்ப்பைக் கண்டறியவும்.
எடுத்துக்காட்டு 9.கலசத்தில் 6 வெள்ளை மற்றும் 4 கருப்பு பந்துகள் உள்ளன. கலசத்திலிருந்து 3 பந்துகள் எடுக்கப்படுகின்றன. வரையப்பட்ட பந்துகளில் உள்ள வெள்ளைப் பந்துகளின் எண்ணிக்கை தனித்த சீரற்ற மாறியாகும் எக்ஸ். இந்த சீரற்ற மாறியின் கணித எதிர்பார்ப்பு மற்றும் மாறுபாட்டைக் கண்டறியவும்.
தீர்வு. சீரற்ற மதிப்பு எக்ஸ் 0, 1, 2, 3 மதிப்புகளை எடுக்கலாம். தொடர்புடைய நிகழ்தகவுகளை இதிலிருந்து கணக்கிடலாம் நிகழ்தகவு பெருக்கல் விதி. சீரற்ற மாறியின் விநியோக விதி:
| எக்ஸ் | 0 | 1 | 2 | 3 |
| ப | 1/30 | 3/10 | 1/2 | 1/6 |
எனவே இந்த சீரற்ற மாறியின் கணித எதிர்பார்ப்பு:
எம்(எக்ஸ்) = 3/10 + 1 + 1/2 = 1,8 .
கொடுக்கப்பட்ட சீரற்ற மாறியின் மாறுபாடு:
டி(எக்ஸ்) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
தொடர்ச்சியான சீரற்ற மாறியின் எதிர்பார்ப்பு மற்றும் மாறுபாடு
தொடர்ச்சியான சீரற்ற மாறிக்கு, கணித எதிர்பார்ப்பின் இயந்திர விளக்கம் அதே பொருளைத் தக்க வைத்துக் கொள்ளும்: அடர்த்தியுடன் x- அச்சில் தொடர்ந்து விநியோகிக்கப்படும் ஒரு அலகு வெகுஜனத்திற்கான வெகுஜன மையம் f(எக்ஸ்) ஒரு தனித்த சீரற்ற மாறி போலல்லாமல், அதன் செயல்பாடு வாதம் எக்ஸ்நான்ஒரு தொடர்ச்சியான சீரற்ற மாறிக்கு திடீரென மாறுகிறது, வாதம் தொடர்ந்து மாறுகிறது. ஆனால் தொடர்ச்சியான சீரற்ற மாறியின் கணித எதிர்பார்ப்பும் அதன் சராசரி மதிப்புடன் தொடர்புடையது.
தொடர்ச்சியான சீரற்ற மாறியின் கணித எதிர்பார்ப்பு மற்றும் மாறுபாட்டைக் கண்டறிய, நீங்கள் திட்டவட்டமான ஒருங்கிணைப்புகளைக் கண்டறிய வேண்டும். . தொடர்ச்சியான சீரற்ற மாறியின் அடர்த்தி செயல்பாடு கொடுக்கப்பட்டால், அது நேரடியாக ஒருங்கிணைப்பில் நுழைகிறது. நிகழ்தகவு பரவல் செயல்பாடு கொடுக்கப்பட்டால், அதை வேறுபடுத்துவதன் மூலம், நீங்கள் அடர்த்தி செயல்பாட்டைக் கண்டறிய வேண்டும்.
தொடர்ச்சியான சீரற்ற மாறியின் சாத்தியமான அனைத்து மதிப்புகளின் எண்கணித சராசரி அதன் என அழைக்கப்படுகிறது கணித எதிர்பார்ப்பு, அல்லது மூலம் குறிக்கப்படுகிறது.
ஒரு தனித்த நிகழ்தகவு இடத்தில் கொடுக்கப்பட்ட ஒரு சீரற்ற மாறி X இன் கணித எதிர்பார்ப்பு (சராசரி மதிப்பு) என்பது தொடர் முழுவதுமாக ஒன்றிணைந்தால் m =M[X]=∑x i p i ஆகும்.
சேவையின் நோக்கம். ஆன்லைன் சேவையைப் பயன்படுத்துதல் கணித எதிர்பார்ப்பு, மாறுபாடு மற்றும் நிலையான விலகல் ஆகியவை கணக்கிடப்படுகின்றன(உதாரணத்தைப் பார்க்கவும்). கூடுதலாக, F(X) விநியோகச் செயல்பாட்டின் வரைபடம் திட்டமிடப்பட்டுள்ளது.
சீரற்ற மாறியின் கணித எதிர்பார்ப்பின் பண்புகள்
- ஒரு நிலையான மதிப்பின் கணித எதிர்பார்ப்பு தனக்குச் சமம்: M[C]=C, C - மாறிலி;
- M=C M[X]
- சீரற்ற மாறிகளின் கூட்டுத்தொகையின் கணித எதிர்பார்ப்பு அவற்றின் கணித எதிர்பார்ப்புகளின் கூட்டுத்தொகைக்கு சமம்: M=M[X]+M[Y]
- சுயாதீன சீரற்ற மாறிகளின் உற்பத்தியின் கணித எதிர்பார்ப்பு அவற்றின் கணித எதிர்பார்ப்புகளின் பெருக்கத்திற்கு சமம்: M=M[X] M[Y] , X மற்றும் Y ஆகியவை சுயாதீனமாக இருந்தால்.
சிதறல் பண்புகள்
- நிலையான மதிப்பின் மாறுபாடு பூஜ்ஜியம்: D(c)=0.
- நிலையான காரணியை ஸ்கொயர் செய்வதன் மூலம் சிதறல் குறியின் கீழ் இருந்து எடுக்கலாம்: D(k*X)= k 2 D(X).
- X மற்றும் Y ஆகிய சீரற்ற மாறிகள் சுயாதீனமாக இருந்தால், கூட்டுத்தொகையின் மாறுபாடு மாறுபாடுகளின் கூட்டுத்தொகைக்கு சமமாக இருக்கும்: D(X+Y)=D(X)+D(Y).
- சீரற்ற மாறிகள் X மற்றும் Y சார்ந்து இருந்தால்: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- பின்வரும் கணக்கீட்டு சூத்திரம் சிதறலுக்கு செல்லுபடியாகும்:
D(X)=M(X 2)-(M(X)) 2
உதாரணமாக. X மற்றும் Y ஆகிய இரண்டு சார்பற்ற சீரற்ற மாறிகளின் கணித எதிர்பார்ப்புகள் மற்றும் மாறுபாடுகள் அறியப்படுகின்றன: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Z=9X-8Y+7 என்ற சீரற்ற மாறியின் கணித எதிர்பார்ப்பு மற்றும் மாறுபாட்டைக் கண்டறியவும்.
தீர்வு. கணித எதிர்பார்ப்பின் பண்புகளின் அடிப்படையில்: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23
சிதறலின் பண்புகளின் அடிப்படையில்: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
கணித எதிர்பார்ப்பைக் கணக்கிடுவதற்கான அல்காரிதம்
தனித்துவமான சீரற்ற மாறிகளின் பண்புகள்: அவற்றின் அனைத்து மதிப்புகளையும் மறுபெயரிடலாம் இயற்கை எண்கள்; ஒவ்வொரு மதிப்பும் பூஜ்ஜியம் அல்லாத நிகழ்தகவுடன் தொடர்புடையது.- ஜோடிகளை ஒவ்வொன்றாகப் பெருக்குகிறோம்: x i ஆல் p i .
- ஒவ்வொரு ஜோடியின் உற்பத்தியையும் x i p i .
எடுத்துக்காட்டாக, n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
எடுத்துக்காட்டு எண். 1.
| x i | 1 | 3 | 4 | 7 | 9 |
| p i | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
m = ∑x i p i சூத்திரத்தைப் பயன்படுத்தி கணித எதிர்பார்ப்பைக் காண்கிறோம்.
எதிர்பார்ப்பு M[X].
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
d = ∑x 2 i p i - M[x] 2 சூத்திரத்தைப் பயன்படுத்தி மாறுபாட்டைக் காண்கிறோம்.
மாறுபாடு D[X].
D[X] = 1 2 *0.1 + 3 2 *0.2 + 4 2 *0.1 + 7 2 *0.3 + 9 2 *0.3 - 5.9 2 = 7.69
நிலையான விலகல் σ(x).
σ = sqrt(D[X]) = sqrt(7.69) = 2.78
எடுத்துக்காட்டு எண். 2. ஒரு தனித்த சீரற்ற மாறி உள்ளது அடுத்த வரிசைவிநியோகங்கள்:
| எக்ஸ் | -10 | -5 | 0 | 5 | 10 |
| ஆர் | ஏ | 0,32 | 2அ | 0,41 | 0,03 |
தீர்வு. a இன் மதிப்பு உறவிலிருந்து கண்டறியப்படுகிறது: Σp i = 1
Σp i = a + 0.32 + 2 a + 0.41 + 0.03 = 0.76 + 3 a = 1
0.76 + 3 a = 1 அல்லது 0.24=3 a , எங்கிருந்து a = 0.08
எடுத்துக்காட்டு எண். 3. ஒரு தனித்த சீரற்ற மாறியின் பரவல் விதியை அதன் மாறுபாடு அறியப்பட்டால் தீர்மானிக்கவும், மற்றும் x 1
ப 1 =0.3; ப 2 =0.3; ப 3 =0.1; ப 4 =0.3
d(x)=12.96
தீர்வு.
d(x) மாறுபாட்டைக் கண்டறிய இங்கே நீங்கள் ஒரு சூத்திரத்தை உருவாக்க வேண்டும்:
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
இதில் எதிர்பார்ப்பு m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
எங்கள் தரவுகளுக்கு
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12.96 = 6 2 0.3+9 2 0.3+x 3 2 0.1+15 2 0.3-(9+0.1x 3) 2
அல்லது -9/100 (x 2 -20x+96)=0
அதன்படி, சமன்பாட்டின் வேர்களை நாம் கண்டுபிடிக்க வேண்டும், அவற்றில் இரண்டு இருக்கும்.
x 3 =8, x 3 =12
நிபந்தனை x 1ஐப் பூர்த்தி செய்யும் ஒன்றைத் தேர்ந்தெடுக்கவும்
ஒரு தனித்த சீரற்ற மாறியின் விநியோக சட்டம்
x 1 =6; x 2 =9; x 3 =12; x 4 =15
ப 1 =0.3; ப 2 =0.3; ப 3 =0.1; ப 4 =0.3
 .
.
மாறாக, எதிர்மறை அல்லாத a.e. போன்ற செயல்பாடு  , பின்னர் அதன் அடர்த்தியில் முற்றிலும் தொடர்ச்சியான நிகழ்தகவு அளவீடு உள்ளது.
, பின்னர் அதன் அடர்த்தியில் முற்றிலும் தொடர்ச்சியான நிகழ்தகவு அளவீடு உள்ளது.
Lebesgue integral இல் அளவை மாற்றுதல்:
 ,
,
நிகழ்தகவு அளவீட்டைப் பொறுத்த வரையில் ஒருங்கிணைக்கக்கூடிய எந்த போரல் செயல்பாடு உள்ளது.
சிதறல், வகைகள் மற்றும் சிதறலின் பண்புகள் சிதறல் கருத்து
புள்ளிவிவரங்களில் சிதறல்எண்கணித சராசரியிலிருந்து வகைப்படுத்தப்பட்ட குணாதிசயத்தின் தனிப்பட்ட மதிப்புகளின் நிலையான விலகலாகக் காணப்படுகிறது. ஆரம்ப தரவைப் பொறுத்து, இது எளிய மற்றும் எடையுள்ள மாறுபாடு சூத்திரங்களைப் பயன்படுத்தி தீர்மானிக்கப்படுகிறது:
1. எளிய மாறுபாடு(தொகுக்கப்படாத தரவுகளுக்கு) சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது:
![]()
2. எடையுள்ள மாறுபாடு (மாறுபாடு தொடர்களுக்கு):

இதில் n என்பது அதிர்வெண் (காரணி X இன் மறுநிகழ்வு)
மாறுபாட்டைக் கண்டறிவதற்கான எடுத்துக்காட்டு
இந்தப் பக்கம் மாறுபாட்டைக் கண்டறிவதற்கான ஒரு நிலையான உதாரணத்தை விவரிக்கிறது, அதைக் கண்டறிவதற்கான பிற சிக்கல்களையும் நீங்கள் பார்க்கலாம்
எடுத்துக்காட்டு 1. குழு, குழு சராசரி, இடைக்குழு மற்றும் மொத்த மாறுபாடு ஆகியவற்றை தீர்மானித்தல்
எடுத்துக்காட்டு 2. ஒரு குழு அட்டவணையில் மாறுபாடு மற்றும் மாறுபாட்டின் குணகம் கண்டறிதல்
எடுத்துக்காட்டு 3. ஒரு தனித் தொடரில் மாறுபாட்டைக் கண்டறிதல்
எடுத்துக்காட்டு 4. பின்வரும் தரவு 20 கடித மாணவர்களின் குழுவிற்கு கிடைக்கிறது. குணாதிசயத்தின் விநியோகத்தின் இடைவெளித் தொடரை உருவாக்குவது, பண்புகளின் சராசரி மதிப்பைக் கணக்கிடுவது மற்றும் அதன் சிதறலைப் படிப்பது அவசியம்.

ஒரு இடைவெளி குழுவை உருவாக்குவோம். சூத்திரத்தைப் பயன்படுத்தி இடைவெளியின் வரம்பை தீர்மானிப்போம்:
![]()
இதில் X max என்பது குழுப் பண்புகளின் அதிகபட்ச மதிப்பு; X நிமிடம் - தொகுத்தல் பண்புகளின் குறைந்தபட்ச மதிப்பு; n - இடைவெளிகளின் எண்ணிக்கை:
நாங்கள் n=5 ஐ ஏற்றுக்கொள்கிறோம். படி: h = (192 - 159)/ 5 = 6.6
ஒரு இடைவெளி குழுவை உருவாக்குவோம்

மேலும் கணக்கீடுகளுக்கு, நாங்கள் ஒரு துணை அட்டவணையை உருவாக்குவோம்:

X"i – இடைவெளியின் நடுப்பகுதி. (உதாரணமாக, இடைவெளியின் நடுப்பகுதி 159 – 165.6 = 162.3)
எடையுள்ள எண்கணித சராசரி சூத்திரத்தைப் பயன்படுத்தி மாணவர்களின் சராசரி உயரத்தை நாங்கள் தீர்மானிக்கிறோம்:

சூத்திரத்தைப் பயன்படுத்தி மாறுபாட்டைத் தீர்மானிப்போம்:
சூத்திரத்தை இவ்வாறு மாற்றலாம்:

இந்த சூத்திரத்திலிருந்து அது பின்வருமாறு மாறுபாடு சமம் விருப்பங்களின் சதுரங்களின் சராசரிக்கும் சதுரத்திற்கும் சராசரிக்கும் இடையிலான வேறுபாடு.
மாறுபாடு தொடரில் சிதறல்கணங்களின் முறையைப் பயன்படுத்தி சம இடைவெளிகளுடன், சிதறலின் இரண்டாவது பண்புகளைப் பயன்படுத்தி பின்வரும் வழியில் கணக்கிடலாம் (அனைத்து விருப்பங்களையும் இடைவெளியின் மதிப்பால் வகுத்தல்). மாறுபாட்டை தீர்மானித்தல், கணங்களின் முறையைப் பயன்படுத்தி கணக்கிடப்படுகிறது, பின்வரும் சூத்திரத்தைப் பயன்படுத்துவது குறைவான உழைப்பு:

i என்பது இடைவெளியின் மதிப்பு; A என்பது ஒரு வழக்கமான பூஜ்ஜியமாகும், இதற்காக அதிக அதிர்வெண் கொண்ட இடைவெளியின் நடுப்பகுதியைப் பயன்படுத்துவது வசதியானது; m1 என்பது முதல் வரிசை தருணத்தின் சதுரம்; m2 - இரண்டாவது வரிசையின் தருணம்
மாற்று பண்பு மாறுபாடு (ஒரு புள்ளியியல் மக்கள்தொகையில் இரண்டு பரஸ்பர பிரத்தியேக விருப்பங்கள் மட்டுமே இருக்கும் வகையில் ஒரு சிறப்பியல்பு மாற்றங்கள் இருந்தால், அத்தகைய மாறுபாடு மாற்று என்று அழைக்கப்படுகிறது) சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்:

இந்த சிதறல் சூத்திரத்தில் q = 1- p ஐ மாற்றினால், நாம் பெறுகிறோம்:

மாறுபாட்டின் வகைகள்
மொத்த மாறுபாடுஇந்த மாறுபாட்டை ஏற்படுத்தும் அனைத்து காரணிகளின் செல்வாக்கின் கீழ் ஒட்டுமொத்த மக்கள்தொகை முழுவதும் ஒரு பண்பு மாறுபாட்டை அளவிடுகிறது. இது x இன் ஒட்டுமொத்த சராசரி மதிப்பிலிருந்து ஒரு குணாதிசயமான x இன் தனிப்பட்ட மதிப்புகளின் விலகல்களின் சராசரி சதுரத்திற்குச் சமம் மற்றும் எளிய மாறுபாடு அல்லது எடையுள்ள மாறுபாடு என வரையறுக்கலாம்.
குழுவிற்குள் மாறுபாடு சீரற்ற மாறுபாட்டை வகைப்படுத்துகிறது, அதாவது. கணக்கிடப்படாத காரணிகளின் செல்வாக்கின் காரணமாக ஏற்படும் மாறுபாட்டின் ஒரு பகுதி மற்றும் குழுவின் அடிப்படையை உருவாக்கும் காரணி-பண்பு சார்ந்து இல்லை. இத்தகைய சிதறல் குழுவின் எண்கணித சராசரியிலிருந்து குழு X க்குள் உள்ள பண்புக்கூறின் தனிப்பட்ட மதிப்புகளின் விலகல்களின் சராசரி சதுரத்திற்கு சமம் மற்றும் எளிய சிதறல் அல்லது எடையுள்ள சிதறல் என கணக்கிடலாம்.
இதனால், குழுவிற்குள் மாறுபாடு நடவடிக்கைகள்ஒரு குழுவிற்குள் ஒரு பண்பின் மாறுபாடு மற்றும் சூத்திரத்தால் தீர்மானிக்கப்படுகிறது:

xi என்பது குழு சராசரி; ni என்பது குழுவில் உள்ள அலகுகளின் எண்ணிக்கை.
எடுத்துக்காட்டாக, ஒரு பட்டறையில் தொழிலாளர் உற்பத்தித்திறன் மட்டத்தில் தொழிலாளர் தகுதிகளின் செல்வாக்கைப் படிக்கும் பணியில் தீர்மானிக்கப்பட வேண்டிய உள்குழு மாறுபாடுகள் ஒவ்வொரு குழுவிலும் சாத்தியமான அனைத்து காரணிகளாலும் ஏற்படும் வெளியீட்டில் மாறுபாடுகளைக் காட்டுகின்றன (உபகரணங்களின் தொழில்நுட்ப நிலை, கிடைக்கும் தன்மை கருவிகள் மற்றும் பொருட்கள், தொழிலாளர்களின் வயது, உழைப்பு தீவிரம் போன்றவை. .), தகுதி வகை வேறுபாடுகள் தவிர (ஒரு குழுவிற்குள் அனைத்து தொழிலாளர்களுக்கும் ஒரே தகுதிகள் உள்ளன).
குழுவிற்குள் உள்ள மாறுபாடுகளின் சராசரி சீரற்ற மாறுபாட்டை பிரதிபலிக்கிறது, அதாவது, குழுவாகும் காரணியைத் தவிர, மற்ற எல்லா காரணிகளின் செல்வாக்கின் கீழ் ஏற்பட்ட மாறுபாட்டின் ஒரு பகுதி. இது சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது:

இடைக்குழு மாறுபாடுஇதன் விளைவாக வரும் பண்புகளின் முறையான மாறுபாட்டை வகைப்படுத்துகிறது, இது குழுவின் அடிப்படையை உருவாக்கும் காரணி-பண்பின் செல்வாக்கின் காரணமாகும். இது குழுவின் ஒட்டுமொத்த சராசரியிலிருந்து விலகல்களின் சராசரி சதுரத்திற்கு சமம். இன்டர்குரூப் மாறுபாடு சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது:

