மேட்ரிக்ஸின் தரவரிசை என்ன. மேட்ரிக்ஸ் ரேங்க் மற்றும் மேட்ரிக்ஸ் அடிப்படையில் மைனர்

மேட்ரிக்ஸின் தரவரிசை ஒரு முக்கியமான எண் பண்பு ஆகும். மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிவதில் மிகவும் பொதுவான சிக்கல் நேரியல் இயற்கணித சமன்பாடுகளின் அமைப்பின் நிலைத்தன்மையை சரிபார்க்கிறது. இந்த கட்டுரையில் மேட்ரிக்ஸ் தரவரிசையின் கருத்தை வழங்குவோம் மற்றும் அதைக் கண்டுபிடிப்பதற்கான முறைகளைக் கருத்தில் கொள்வோம். பொருளை நன்கு புரிந்துகொள்ள, பல எடுத்துக்காட்டுகளுக்கான தீர்வுகளை விரிவாக ஆராய்வோம்.

பக்க வழிசெலுத்தல்.

மேட்ரிக்ஸின் தரத்தை தீர்மானித்தல் மற்றும் தேவையான கூடுதல் கருத்துகள்.

மேட்ரிக்ஸின் ரேங்க் வரையறைக்கு குரல் கொடுப்பதற்கு முன், மைனர் என்ற கருத்தை நீங்கள் நன்கு புரிந்து கொள்ள வேண்டும், மேலும் மேட்ரிக்ஸின் மைனர்களைக் கண்டறிவது தீர்மானிப்பதைக் கணக்கிடும் திறனைக் குறிக்கிறது. எனவே, தேவைப்பட்டால், கட்டுரையின் கோட்பாடு, மேட்ரிக்ஸின் தீர்மானிப்பதைக் கண்டறியும் முறைகள் மற்றும் தீர்மானிப்பவரின் பண்புகளை நீங்கள் நினைவுபடுத்த பரிந்துரைக்கிறோம்.

ஒரு அணி A வரிசையை எடுத்துக் கொள்வோம். k சிலவாக இருக்கட்டும் இயற்கை எண், m மற்றும் n எண்களில் மிகச்சிறியதை விட அதிகமாக இல்லை, அதாவது, .

வரையறை.

சிறிய kth ஆர்டர்அணி A என்பது ஒரு சதுர மேட்ரிக்ஸின் நிர்ணயம் ஆகும், இது அணி A இன் உறுப்புகளால் ஆனது, அவை முன்பே தேர்ந்தெடுக்கப்பட்ட k வரிசைகள் மற்றும் k நெடுவரிசைகளில் அமைந்துள்ளன, மேலும் அணி A இன் உறுப்புகளின் அமைப்பு பாதுகாக்கப்படுகிறது.

வேறு வார்த்தைகளில் கூறுவதானால், அணி A இல் நாம் (p-k) வரிசைகள் மற்றும் (n-k) நெடுவரிசைகளை நீக்கினால், மீதமுள்ள உறுப்புகளிலிருந்து ஒரு அணியை உருவாக்கி, அணி A இன் உறுப்புகளின் அமைப்பைப் பாதுகாத்தால், பின்னர் இதன் விளைவாக வரும் அணி, அணி A இன் k வரிசையின் மைனர் ஆகும்.

ஒரு உதாரணத்தைப் பயன்படுத்தி மேட்ரிக்ஸ் மைனரின் வரையறையைப் பார்ப்போம்.

மேட்ரிக்ஸைக் கவனியுங்கள் .

இந்த மேட்ரிக்ஸின் பல முதல்-வரிசை மைனர்களை எழுதுவோம். எடுத்துக்காட்டாக, அணி A இன் மூன்றாவது வரிசை மற்றும் இரண்டாவது நெடுவரிசையைத் தேர்வுசெய்தால், எங்கள் தேர்வு முதல்-வரிசை மைனருக்கு ஒத்திருக்கும் . வேறு வார்த்தைகளில் கூறுவதானால், இந்த மைனரைப் பெற, நாங்கள் முதல் மற்றும் இரண்டாவது வரிசைகளையும், மேட்ரிக்ஸ் A இலிருந்து முதல், மூன்றாவது மற்றும் நான்காவது நெடுவரிசைகளையும் கடந்து, மீதமுள்ள உறுப்பிலிருந்து ஒரு தீர்மானத்தை உருவாக்கினோம். மேட்ரிக்ஸ் A இன் முதல் வரிசை மற்றும் மூன்றாவது நெடுவரிசையைத் தேர்வுசெய்தால், நமக்கு ஒரு மைனர் கிடைக்கும் .

கருதப்படும் முதல்-வரிசை சிறார்களைப் பெறுவதற்கான நடைமுறையை விளக்குவோம்
மற்றும் .

எனவே, மேட்ரிக்ஸின் முதல்-வரிசை மைனர்கள் மேட்ரிக்ஸ் கூறுகளாகும்.

பல இரண்டாம் நிலை மைனர்களைக் காட்டுவோம். இரண்டு வரிசைகள் மற்றும் இரண்டு நெடுவரிசைகளைத் தேர்ந்தெடுக்கவும். உதாரணமாக, முதல் மற்றும் இரண்டாவது வரிசைகள் மற்றும் மூன்றாவது மற்றும் நான்காவது நெடுவரிசைகளை எடுத்துக் கொள்ளுங்கள். இந்தத் தேர்வின் மூலம் எங்களிடம் இரண்டாவது வரிசை மைனர் இருக்கிறார் . மேட்ரிக்ஸ் ஏ இலிருந்து மூன்றாவது வரிசை, முதல் மற்றும் இரண்டாவது நெடுவரிசைகளை நீக்குவதன் மூலமும் இந்த மைனர் உருவாக்கப்படலாம்.

அணி A இன் மற்றொரு இரண்டாம்-வரிசை மைனர் .

இந்த இரண்டாம் நிலை சிறார்களின் கட்டுமானத்தை விளக்குவோம்
மற்றும் .

இதேபோல், அணி A இன் மூன்றாம் வரிசை மைனர்களைக் காணலாம். மேட்ரிக்ஸ் A இல் மூன்று வரிசைகள் மட்டுமே இருப்பதால், அனைத்தையும் தேர்ந்தெடுக்கிறோம். இந்த வரிசைகளின் முதல் மூன்று நெடுவரிசைகளைத் தேர்ந்தெடுத்தால், மூன்றாம் வரிசை மைனர் கிடைக்கும்

மேட்ரிக்ஸ் A இன் கடைசி நெடுவரிசையைக் கடப்பதன் மூலமும் இதை உருவாக்கலாம்.

மற்றொரு மூன்றாவது ஆர்டர் மைனர்

அணி A இன் மூன்றாவது நெடுவரிசையை நீக்குவதன் மூலம் பெறப்பட்டது.

இந்த மூன்றாம் வரிசை சிறார்களின் கட்டுமானத்தைக் காட்டும் படம் இங்கே உள்ளது
மற்றும் .

கொடுக்கப்பட்ட அணி A க்கு, மூன்றை விட அதிக மைனர்கள் இல்லை.

வரிசையின் அணி A இல் kth வரிசையில் எத்தனை மைனர்கள் உள்ளனர்?

வரிசை k இன் மைனர்களின் எண்ணிக்கை , எங்கே என கணக்கிடலாம் மற்றும் - முறையே p இலிருந்து k மற்றும் n இலிருந்து k வரையிலான சேர்க்கைகளின் எண்ணிக்கை.

மேட்ரிக்ஸ் A வரிசையின் அனைத்து மைனர்களையும் n ஆல் p வரிசையை எவ்வாறு உருவாக்குவது?

எங்களுக்கு பல அணி வரிசை எண்கள் மற்றும் பல நெடுவரிசை எண்கள் தேவைப்படும். நாங்கள் எல்லாவற்றையும் எழுதுகிறோம் கே மூலம் p உறுப்புகளின் சேர்க்கைகள்(ஒரு சிறிய வரிசை k ஐ உருவாக்கும்போது அவை அணி A இன் தேர்ந்தெடுக்கப்பட்ட வரிசைகளுடன் ஒத்திருக்கும்). வரிசை எண்களின் ஒவ்வொரு கலவையிலும், k நெடுவரிசை எண்களின் n உறுப்புகளின் அனைத்து சேர்க்கைகளையும் வரிசையாகச் சேர்க்கிறோம். அணி A இன் வரிசை எண்கள் மற்றும் நெடுவரிசை எண்களின் சேர்க்கைகளின் இந்த தொகுப்புகள், வரிசையின் அனைத்து மைனர்களையும் உருவாக்க உதவும்.

அதை ஒரு உதாரணத்துடன் பார்ப்போம்.

உதாரணமாக.

மேட்ரிக்ஸின் அனைத்து இரண்டாம் வரிசை சிறார்களையும் கண்டறியவும்.

தீர்வு.

அசல் மேட்ரிக்ஸின் வரிசை 3 ஆல் 3 ஆக இருப்பதால், இரண்டாவது வரிசை மைனர்களின் மொத்த எண்ணிக்கை இருக்கும் .

அணி A: 1, 2 இன் 3 முதல் 2 வரிசை எண்களின் அனைத்து சேர்க்கைகளையும் எழுதுவோம்; 1, 3 மற்றும் 2, 3. 3 முதல் 2 நெடுவரிசை எண்களின் அனைத்து சேர்க்கைகளும் 1, 2; 1, 3 மற்றும் 2, 3.

அணி A இன் முதல் மற்றும் இரண்டாவது வரிசைகளை எடுத்துக் கொள்வோம். இந்த வரிசைகளுக்கான முதல் மற்றும் இரண்டாவது நெடுவரிசைகள், முதல் மற்றும் மூன்றாவது நெடுவரிசைகள், இரண்டாவது மற்றும் மூன்றாவது நெடுவரிசைகளைத் தேர்ந்தெடுப்பதன் மூலம், முறையே சிறார்களைப் பெறுகிறோம்.

முதல் மற்றும் மூன்றாவது வரிசைகளுக்கு, ஒரே மாதிரியான நெடுவரிசைகளுடன், எங்களிடம் உள்ளது

இரண்டாவது மற்றும் மூன்றாவது வரிசைகளில் முதல் மற்றும் இரண்டாவது, முதல் மற்றும் மூன்றாவது, இரண்டாவது மற்றும் மூன்றாவது நெடுவரிசைகளைச் சேர்க்க இது உள்ளது:

எனவே, அணி A இன் ஒன்பது இரண்டாம் வரிசை மைனர்களும் கண்டுபிடிக்கப்பட்டுள்ளனர்.

இப்போது நாம் மேட்ரிக்ஸின் தரத்தை தீர்மானிக்க தொடரலாம்.

வரையறை.

மேட்ரிக்ஸ் தரவரிசைமேட்ரிக்ஸின் பூஜ்ஜியமற்ற மைனரின் மிக உயர்ந்த வரிசையாகும்.

அணி A இன் ரேங்க் ரேங்க்(A) எனக் குறிக்கப்படுகிறது. Rg(A) அல்லது Rang(A) என்ற பெயர்களையும் நீங்கள் காணலாம்.

மேட்ரிக்ஸ் ரேங்க் மற்றும் மேட்ரிக்ஸ் மைனர் ஆகியவற்றின் வரையறைகளிலிருந்து, பூஜ்ஜிய மேட்ரிக்ஸின் தரவரிசை பூஜ்ஜியத்திற்கு சமம் என்றும், பூஜ்ஜியமற்ற மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்குக் குறையாது என்றும் முடிவு செய்யலாம்.

வரையறையின்படி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிதல்.

எனவே, மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிவதற்கான முதல் முறை சிறார்களை கணக்கிடும் முறை. இந்த முறை மேட்ரிக்ஸின் தரத்தை நிர்ணயிப்பதை அடிப்படையாகக் கொண்டது.

வரிசையின் அணி A இன் தரவரிசையை நாம் கண்டுபிடிக்க வேண்டும்.

சுருக்கமாக விவரிப்போம் அல்காரிதம்சிறார்களைக் கணக்கிடுவதன் மூலம் இந்த சிக்கலைத் தீர்ப்பது.

பூஜ்ஜியத்திலிருந்து வேறுபட்ட மேட்ரிக்ஸின் குறைந்தபட்சம் ஒரு உறுப்பு இருந்தால், மேட்ரிக்ஸின் தரவரிசை குறைந்தபட்சம் ஒன்றுக்கு சமமாக இருக்கும் (பூஜ்ஜியத்திற்கு சமமாக இல்லாத முதல்-வரிசை மைனர் இருப்பதால்).

அடுத்து நாம் இரண்டாவது வரிசை சிறார்களைப் பார்க்கிறோம். அனைத்து இரண்டாம் வரிசை மைனர்களும் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்கு சமம். இரண்டாவது வரிசையில் பூஜ்ஜியமற்ற மைனர் ஒன்று இருந்தால், நாங்கள் மூன்றாவது வரிசையின் சிறார்களைக் கணக்கிடுகிறோம், மேலும் மேட்ரிக்ஸின் தரம் குறைந்தது இரண்டுக்கு சமமாக இருக்கும்.

இதேபோல், அனைத்து மூன்றாம் வரிசை மைனர்களும் பூஜ்ஜியமாக இருந்தால், மேட்ரிக்ஸின் தரவரிசை இரண்டு. பூஜ்ஜியத்தைத் தவிர குறைந்தபட்சம் ஒரு மூன்றாம் வரிசை மைனர் இருந்தால், மேட்ரிக்ஸின் ரேங்க் குறைந்தது மூன்று ஆகும், மேலும் நான்காவது வரிசை மைனர்களைக் கணக்கிடுவதற்கு நாங்கள் செல்கிறோம்.

மேட்ரிக்ஸின் தரவரிசை p மற்றும் n எண்களில் மிகச்சிறியதை விட அதிகமாக இருக்கக்கூடாது என்பதை நினைவில் கொள்க.

உதாரணமாக.

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும் .

தீர்வு.

அணி பூஜ்ஜியமாக இல்லாததால், அதன் தரவரிசை ஒன்றுக்கு குறைவாக இல்லை.

இரண்டாவது வரிசையில் சிறியது பூஜ்ஜியத்திலிருந்து வேறுபட்டது, எனவே, அணி A இன் தரவரிசை குறைந்தது இரண்டு ஆகும். மூன்றாம் வரிசை சிறார்களைக் கணக்கிடுவதற்கு நாங்கள் செல்கிறோம். அவர்கள் மொத்தம் விஷயங்கள்.

அனைத்து மூன்றாம் வரிசை சிறார்களும் பூஜ்ஜியத்திற்கு சமம். எனவே, மேட்ரிக்ஸின் தரவரிசை இரண்டு.

பதில்:

ரேங்க்(A) = 2 .

சிறார்களை எல்லைப்படுத்தும் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிதல்.

ஒரு மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிவதற்கான பிற முறைகள் உள்ளன, அவை குறைந்த கணக்கீட்டு வேலைகளுடன் முடிவைப் பெற உங்களை அனுமதிக்கின்றன.

அத்தகைய ஒரு முறை விளிம்பு சிறிய முறை.

சமாளிப்போம் விளிம்பு சிறிய கருத்து.

மைனர் M ok உடன் தொடர்புடைய அணி மைனருடன் தொடர்புடைய அணியை "கொண்டிருந்தால்" அணி A இன் (k+1) வது வரிசையின் மைனர் M ok, அணி A இன் மைனர் M வரிசை k எல்லையாக இருக்கும் என்று கூறப்படுகிறது. எம் .

வேறு வார்த்தைகளில் கூறுவதானால், ஒரு வரிசை மற்றும் ஒரு நெடுவரிசையின் கூறுகளை நீக்குவதன் மூலம், எல்லையான மைனர் M உடன் தொடர்புடைய அணியானது, மைனர் M ok உடன் தொடர்புடைய அணியிலிருந்து பெறப்படுகிறது.

எடுத்துக்காட்டாக, மேட்ரிக்ஸைக் கவனியுங்கள் இரண்டாவது ஆர்டரை மைனர் எடுக்கவும். எல்லைக்குட்பட்ட அனைத்து சிறார்களையும் எழுதுவோம்:

சிறார்களை எல்லைக்குட்படுத்தும் முறை பின்வரும் தேற்றத்தால் நியாயப்படுத்தப்படுகிறது (ஆதாரம் இல்லாமல் அதன் உருவாக்கத்தை நாங்கள் முன்வைக்கிறோம்).

தேற்றம்.

n ஆல் p வரிசையின் ஒரு அணி A இன் kth வரிசை மைனர் எல்லையில் உள்ள அனைத்து மைனர்களும் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், அணி A இன் அனைத்து மைனர்களும் (k+1) பூஜ்ஜியத்திற்கு சமம்.

எனவே, ஒரு மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிய, போதுமான அளவு எல்லையில் இருக்கும் அனைத்து சிறார்களையும் பார்க்க வேண்டிய அவசியமில்லை. ஒரு அணி A வரிசையின் kth வரிசையின் மைனரின் எல்லையில் உள்ள சிறார்களின் எண்ணிக்கை, சூத்திரத்தால் கண்டறியப்படுகிறது . அணி A இன் (k + 1) வரிசை மைனர்களை விட அணி A இன் kth வரிசை மைனர் எல்லையில் மைனர்கள் இல்லை என்பதை நினைவில் கொள்ளவும். எனவே, பெரும்பாலான சந்தர்ப்பங்களில், அனைத்து சிறார்களையும் வெறுமனே கணக்கிடுவதை விட எல்லைக்குட்பட்ட சிறார்களின் முறையைப் பயன்படுத்துவது மிகவும் லாபகரமானது.

சிறார்களை எல்லைப்படுத்தும் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டுபிடிப்பதற்குச் செல்லலாம். சுருக்கமாக விவரிப்போம் அல்காரிதம்இந்த முறை.

அணி A பூஜ்ஜியமற்றதாக இருந்தால், முதல்-வரிசை மைனராக, பூஜ்ஜியத்திலிருந்து வேறுபட்ட அணி A இன் எந்த உறுப்புகளையும் எடுத்துக்கொள்கிறோம். அதன் எல்லைக்குட்பட்ட சிறார்களைப் பார்ப்போம். அவை அனைத்தும் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்கு சமம். குறைந்தபட்சம் ஒரு பூஜ்ஜியமற்ற எல்லை மைனர் இருந்தால் (அதன் வரிசை இரண்டு), அதன் எல்லை மைனர்களை நாங்கள் பரிசீலிக்கிறோம். அவை அனைத்தும் பூஜ்ஜியமாக இருந்தால், தரவரிசை(A) = 2. குறைந்தபட்சம் ஒரு எல்லை மைனர் பூஜ்ஜியம் அல்லாததாக இருந்தால் (அதன் வரிசை மூன்று), அதன் எல்லை மைனர்களை நாங்கள் கருதுகிறோம். மற்றும் பல. இதன் விளைவாக, அணி A இன் (k + 1) வது வரிசையின் அனைத்து எல்லை மைனர்களும் பூஜ்ஜியத்திற்குச் சமமாக இருந்தால் ரேங்க்(A) = k அல்லது ரேங்க்(A) = min(p, n) அல்லாதது இருந்தால் பூஜ்ஜிய சிறிய வரிசையின் சிறிய எல்லை (நிமிடம்(p, n) - 1) .

ஒரு உதாரணத்தைப் பயன்படுத்தி மேட்ரிக்ஸின் தரத்தைக் கண்டறிய சிறார்களை எல்லைப்படுத்தும் முறையைப் பார்ப்போம்.

உதாரணமாக.

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும் சிறார்களை எல்லைப்படுத்தும் முறை மூலம்.

தீர்வு.

அணி A இன் 1 1 உறுப்பு பூஜ்ஜியமற்றதாக இருப்பதால், அதை முதல்-வரிசை மைனராக எடுத்துக்கொள்வோம். பூஜ்ஜியத்திலிருந்து வேறுபட்ட எல்லைக்குட்பட்ட மைனரைத் தேடத் தொடங்குவோம்:

பூஜ்ஜியத்திலிருந்து வேறுபட்ட இரண்டாவது வரிசையின் விளிம்பு மைனர் காணப்படுகிறது. அதன் எல்லைக்குட்பட்ட சிறார்களைப் பார்ப்போம் (அவர்களின் விஷயங்கள்):

இரண்டாவது-வரிசை மைனரின் எல்லையில் உள்ள அனைத்து மைனர்களும் பூஜ்ஜியத்திற்கு சமம், எனவே, அணி A இன் ரேங்க் இரண்டுக்கு சமம்.

பதில்:

ரேங்க்(A) = 2 .

உதாரணமாக.

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும் எல்லைக்குட்பட்ட சிறார்களைப் பயன்படுத்துதல்.

தீர்வு.

முதல் வரிசையின் பூஜ்ஜியமற்ற மைனராக, அணி A இன் 1 1 = 1 உறுப்பை எடுத்துக்கொள்கிறோம். இரண்டாவது வரிசையைச் சுற்றியுள்ள மைனர் பூஜ்ஜியத்திற்கு சமமாக இல்லை. இந்த மைனர் மூன்றாம் வரிசை மைனரால் எல்லையில் உள்ளது
. இது பூஜ்ஜியத்திற்குச் சமமாக இல்லாததாலும், அதற்கு ஒற்றை எல்லையான மைனர் இல்லாததாலும், அணி A இன் ரேங்க் மூன்றுக்கு சமம்.

பதில்:

ரேங்க்(A) = 3 .

எலிமெண்டரி மேட்ரிக்ஸ் மாற்றங்களைப் பயன்படுத்தி தரவரிசையைக் கண்டறிதல் (காஸ் முறை).

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிய மற்றொரு வழியைக் கருத்தில் கொள்வோம்.

பின்வரும் மேட்ரிக்ஸ் மாற்றங்கள் அடிப்படை என அழைக்கப்படுகின்றன:

• மேட்ரிக்ஸின் வரிசைகளை (அல்லது நெடுவரிசைகளை) மறுசீரமைத்தல்;
• ஒரு அணியின் எந்த வரிசையின் (நெடுவரிசை) அனைத்து கூறுகளையும் பூஜ்ஜியத்திலிருந்து வேறுபட்ட தன்னிச்சையான எண் k ஆல் பெருக்குதல்;
• ஒரு வரிசையின் உறுப்புகளுடன் (நெடுவரிசை) மற்றொரு வரிசையின் (நெடுவரிசை) தொடர்புடைய உறுப்புகளைச் சேர்ப்பது, ஒரு தன்னிச்சையான எண் k ஆல் பெருக்கப்படுகிறது.

மேட்ரிக்ஸ் பி என்பது மேட்ரிக்ஸ் ஏ க்கு சமமானதாக அழைக்கப்படுகிறது, ஒரு வரையறுக்கப்பட்ட எண்ணைப் பயன்படுத்தி A இலிருந்து B பெறப்பட்டால் அடிப்படை மாற்றங்கள். மெட்ரிக்குகளின் சமன்பாடு "~" என்ற குறியீட்டால் குறிக்கப்படுகிறது, அதாவது A ~ B என்று எழுதப்பட்டுள்ளது.

எலிமெண்டரி மேட்ரிக்ஸ் உருமாற்றங்களைப் பயன்படுத்தி ஒரு மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிவது இந்த அறிக்கையின் அடிப்படையில் அமைந்துள்ளது: மேட்ரிக்ஸ் B ஆனது மேட்ரிக்ஸ் A இலிருந்து வரையறுக்கப்பட்ட எண்ணிக்கையிலான அடிப்படை மாற்றங்களைப் பயன்படுத்தி பெறப்பட்டால், ரேங்க்(A) = Rank(B) .

இந்த அறிக்கையின் செல்லுபடியாகும் மேட்ரிக்ஸின் நிர்ணயிப்பாளரின் பண்புகளில் இருந்து பின்வருமாறு:

• மேட்ரிக்ஸின் வரிசைகளை (அல்லது நெடுவரிசைகளை) மறுசீரமைக்கும்போது, ​​அதன் தீர்மானிப்பான் அடையாளத்தை மாற்றுகிறது. இது பூஜ்ஜியத்திற்கு சமமாக இருந்தால், வரிசைகள் (நெடுவரிசைகள்) மறுசீரமைக்கப்படும் போது, ​​அது பூஜ்ஜியத்திற்கு சமமாக இருக்கும்.
• மேட்ரிக்ஸின் எந்த வரிசையின் (நெடுவரிசை) அனைத்து உறுப்புகளையும் பூஜ்ஜியத்தைத் தவிர தன்னிச்சையான எண் k ஆல் பெருக்கும்போது, ​​அதன் விளைவாக வரும் மேட்ரிக்ஸின் நிர்ணயிப்பானது k ஆல் பெருக்கப்படும் அசல் மேட்ரிக்ஸின் நிர்ணயிப்பிற்கு சமமாக இருக்கும். அசல் மேட்ரிக்ஸின் நிர்ணயம் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், எந்த வரிசை அல்லது நெடுவரிசையின் அனைத்து கூறுகளையும் k எண்ணால் பெருக்கினால், அதன் விளைவாக வரும் மேட்ரிக்ஸின் தீர்மானகரும் பூஜ்ஜியத்திற்கு சமமாக இருக்கும்.
• மேட்ரிக்ஸின் ஒரு குறிப்பிட்ட வரிசையின் (நெடுவரிசை) உறுப்புகளுடன் மேட்ரிக்ஸின் மற்றொரு வரிசையின் (நெடுவரிசை) தொடர்புடைய உறுப்புகளைச் சேர்ப்பது, ஒரு குறிப்பிட்ட எண்ணால் பெருக்கப்படும் k, அதன் தீர்மானிப்பதை மாற்றாது.

அடிப்படை மாற்றங்களின் முறையின் சாராம்சம்அடிப்படை மாற்றங்களைப் பயன்படுத்தி ஒரு ட்ரெப்சாய்டல் ஒன்றிற்கு (குறிப்பிட்ட வழக்கில், மேல் முக்கோணத்திற்கு) நாம் கண்டுபிடிக்க வேண்டிய மேட்ரிக்ஸைக் குறைப்பதில் உள்ளது.

இது ஏன் செய்யப்படுகிறது? இந்த வகை மெட்ரிக்குகளின் தரவரிசை கண்டுபிடிக்க மிகவும் எளிதானது. குறைந்தபட்சம் ஒரு பூஜ்ஜியமற்ற உறுப்பு கொண்டிருக்கும் வரிகளின் எண்ணிக்கைக்கு இது சமம். அடிப்படை மாற்றங்களைச் செய்யும்போது மேட்ரிக்ஸின் தரவரிசை மாறாது என்பதால், இதன் விளைவாக வரும் மதிப்பு அசல் மேட்ரிக்ஸின் தரமாக இருக்கும்.

மெட்ரிக்குகளின் விளக்கப்படங்களை நாங்கள் தருகிறோம், அவற்றில் ஒன்று மாற்றங்களுக்குப் பிறகு பெறப்பட வேண்டும். அவற்றின் தோற்றம் மேட்ரிக்ஸின் வரிசையைப் பொறுத்தது.

இந்த விளக்கப்படங்கள் மேட்ரிக்ஸ் A ஐ மாற்றும் வார்ப்புருக்கள்.

விவரிப்போம் முறை அல்காரிதம்.

வரிசையின் பூஜ்ஜியமற்ற அணி A இன் தரவரிசையை நாம் கண்டுபிடிக்க வேண்டும் (p என்பது nக்கு சமமாக இருக்கலாம்).

அதனால், . அணி A இன் முதல் வரிசையின் அனைத்து கூறுகளையும் ஆல் பெருக்குவோம். இந்த வழக்கில், நாம் ஒரு சமமான மேட்ரிக்ஸைப் பெறுகிறோம், அதை A (1) குறிக்கிறது:

இதன் விளைவாக வரும் அணி A (1) இன் இரண்டாவது வரிசையின் உறுப்புகளுக்கு, முதல் வரிசையின் தொடர்புடைய கூறுகளை பெருக்குவோம். மூன்றாவது வரியின் உறுப்புகளுக்கு, முதல் வரியின் தொடர்புடைய கூறுகளைச் சேர்த்து, பெருக்கப்படுகிறது. மற்றும் p-th வரி வரை. சமமான மேட்ரிக்ஸைப் பெறுவோம், அதை A (2) குறிக்கவும்:

இதன் விளைவாக வரும் மேட்ரிக்ஸின் அனைத்து கூறுகளும் இரண்டாவது முதல் p-வது வரையிலான வரிசைகளில் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், இந்த மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்கு சமமாக இருக்கும், இதன் விளைவாக, அசல் மேட்ரிக்ஸின் தரவரிசை சமமாக இருக்கும். ஒருவருக்கு.

இரண்டாவது முதல் p-th வரையிலான வரிகளில் குறைந்தது ஒரு பூஜ்ஜியமற்ற உறுப்பு இருந்தால், நாங்கள் தொடர்ந்து மாற்றங்களைச் செய்கிறோம். மேலும், நாங்கள் முற்றிலும் அதே வழியில் செயல்படுகிறோம், ஆனால் படத்தில் குறிக்கப்பட்ட அணி A (2) இன் பகுதியுடன் மட்டுமே.

என்றால், அணி A (2) இன் வரிசைகள் மற்றும் (அல்லது) நெடுவரிசைகளை மறுசீரமைப்போம், இதனால் "புதிய" உறுப்பு பூஜ்ஜியமாக இல்லை.

சில மேட்ரிக்ஸ் கொடுக்கலாம்:

.

இந்த மேட்ரிக்ஸில் தேர்ந்தெடுப்போம் தன்னிச்சையான சரங்கள் மற்றும் தன்னிச்சையான நெடுவரிசைகள்
. பின்னர் தீர்மானிப்பவர் வது வரிசை, அணி உறுப்புகளால் ஆனது
, தேர்ந்தெடுக்கப்பட்ட வரிசைகள் மற்றும் நெடுவரிசைகளின் குறுக்குவெட்டில் அமைந்துள்ளது, இது மைனர் என்று அழைக்கப்படுகிறது வது வரிசை அணி
.

வரையறை 1.13.மேட்ரிக்ஸ் தரவரிசை
இந்த மேட்ரிக்ஸின் பூஜ்ஜியமற்ற மைனரின் மிகப்பெரிய வரிசையாகும்.

மேட்ரிக்ஸின் தரவரிசையைக் கணக்கிட, அதன் அனைத்து சிறார்களையும் மிகக் குறைந்த வரிசையாகக் கருத்தில் கொள்ள வேண்டும், அவற்றில் குறைந்தபட்சம் ஒன்று பூஜ்ஜியத்திலிருந்து வேறுபட்டால், உயர்ந்த வரிசையின் சிறார்களைக் கருத்தில் கொள்ள வேண்டும். மேட்ரிக்ஸின் தரத்தை நிர்ணயிப்பதற்கான இந்த அணுகுமுறை எல்லை முறை (அல்லது சிறார்களை எல்லைப்படுத்தும் முறை) என்று அழைக்கப்படுகிறது.

சிக்கல் 1.4.சிறார்களை எல்லைப்படுத்தும் முறையைப் பயன்படுத்தி, மேட்ரிக்ஸின் தரத்தை தீர்மானிக்கவும்
.

.

எடுத்துக்காட்டாக, முதல்-வரிசை விளிம்பைக் கவனியுங்கள்,
. சில இரண்டாம் வரிசை விளிம்புகளைக் கருத்தில் கொள்ள நாங்கள் செல்கிறோம்.

உதாரணத்திற்கு,
.

இறுதியாக, மூன்றாம் வரிசை எல்லையை பகுப்பாய்வு செய்வோம்.

.

எனவே பூஜ்ஜியம் அல்லாத மைனரின் அதிகபட்ச வரிசை 2 ஆகும், எனவே
.

சிக்கல் 1.4 ஐத் தீர்க்கும் போது, ​​பல இரண்டாம் வரிசை சிறார்களின் எண்ணிக்கை பூஜ்ஜியமாக இருப்பதை நீங்கள் கவனிக்கலாம். இது சம்பந்தமாக, பின்வரும் கருத்து பொருந்தும்.

வரையறை 1.14.மேட்ரிக்ஸின் அடிப்படை மைனர் என்பது பூஜ்ஜியமற்ற மைனர் ஆகும், அதன் வரிசை மேட்ரிக்ஸின் தரத்திற்கு சமம்.

தேற்றம் 1.2.(அடிப்படை சிறு தேற்றம்). அடிப்படை வரிசைகள் (அடிப்படை நெடுவரிசைகள்) நேரியல் சார்புடையவை.

மேட்ரிக்ஸின் வரிசைகள் (நெடுவரிசைகள்) நேரியல் சார்ந்து இருக்கும் என்பதை நினைவில் கொள்ளவும்

தேற்றம் 1.3.நேரியல் சார்பற்ற அணி வரிசைகளின் எண்ணிக்கை நேரியல் சார்பற்ற அணி நெடுவரிசைகளின் எண்ணிக்கைக்கு சமம் மற்றும் மேட்ரிக்ஸின் தரத்திற்கு சமம்.

தேற்றம் 1.4.(தீர்மானி பூஜ்ஜியத்திற்கு சமமாக இருக்க தேவையான மற்றும் போதுமான நிபந்தனை). தீர்மானிப்பதற்காக -வது வரிசை பூஜ்ஜியத்திற்கு சமமாக இருந்தது, அதன் வரிசைகள் (நெடுவரிசைகள்) நேரியல் சார்ந்து இருப்பது அவசியம் மற்றும் போதுமானது.

மேட்ரிக்ஸின் தரவரிசையை அதன் வரையறையின் அடிப்படையில் கணக்கிடுவது மிகவும் சிக்கலானது. உயர் ஆர்டர்களின் மெட்ரிக்குகளுக்கு இது மிகவும் முக்கியமானது. இது சம்பந்தமாக, நடைமுறையில், மேட்ரிக்ஸின் தரவரிசை 10.2 - 10.4 கோட்பாடுகளின் பயன்பாட்டின் அடிப்படையில் கணக்கிடப்படுகிறது, அதே போல் மேட்ரிக்ஸ் சமநிலை மற்றும் அடிப்படை மாற்றங்களின் கருத்துகளின் பயன்பாடு.

வரையறை 1.15.இரண்டு மெட்ரிக்குகள்
மற்றும் அவற்றின் ரேங்க்கள் சமமாக இருந்தால் அவை சமமானவை என்று அழைக்கப்படுகின்றன, அதாவது.
.

மெட்ரிக்ஸ் என்றால்
மற்றும் சமமானவை, பின்னர் கவனிக்கவும்
 .

தேற்றம் 1.5.அடிப்படை மாற்றங்கள் காரணமாக மேட்ரிக்ஸின் தரவரிசை மாறாது.

எலிமெண்டரி மேட்ரிக்ஸ் உருமாற்றங்கள் என்று சொல்வோம்
மேட்ரிக்ஸில் பின்வரும் செயல்பாடுகளில் ஏதேனும்:

வரிசைகளை நெடுவரிசைகள் மற்றும் நெடுவரிசைகளை தொடர்புடைய வரிசைகளுடன் மாற்றுதல்;

மேட்ரிக்ஸ் வரிசைகளை மறுசீரமைத்தல்;

அனைத்து கூறுகளும் பூஜ்ஜியமாக இருக்கும் ஒரு கோட்டைக் கடப்பது;

ஒரு சரத்தை பூஜ்ஜியத்தைத் தவிர வேறு எண்ணால் பெருக்குதல்;

ஒரு வரியின் உறுப்புகளுடன் சேர்த்து மற்றொரு வரியின் தொடர்புடைய உறுப்புகள் அதே எண்ணால் பெருக்கப்படும்
.

தேற்றத்தின் முடிவு 1.5.அணி என்றால்
மேட்ரிக்ஸிலிருந்து பெறப்பட்டது வரையறுக்கப்பட்ட எண்ணிக்கையிலான அடிப்படை மாற்றங்களைப் பயன்படுத்தி, பின்னர் அணி
மற்றும் சமமானவை.

மேட்ரிக்ஸின் தரத்தை கணக்கிடும் போது, ​​வரையறுக்கப்பட்ட எண்ணிக்கையிலான அடிப்படை மாற்றங்களைப் பயன்படுத்தி ஒரு ட்ரெப்சாய்டல் வடிவத்திற்கு குறைக்கப்பட வேண்டும்.

வரையறை 1.16.பூஜ்யம் அல்லாத உயர்ந்த வரிசையின் எல்லைக்குட்பட்ட மைனரில், மூலைவிட்டத்திற்குக் கீழே உள்ள அனைத்து உறுப்புகளும் மறைந்துவிடும் போது, ​​ட்ரெப்சாய்டலை அணி பிரதிநிதித்துவத்தின் ஒரு வடிவம் என்று அழைப்போம். உதாரணத்திற்கு:

.

இங்கே
, அணி உறுப்புகள்
பூஜ்ஜியத்திற்கு செல்க. அத்தகைய மேட்ரிக்ஸின் பிரதிநிதித்துவ வடிவம் ட்ரெப்சாய்டலாக இருக்கும்.

ஒரு விதியாக, காஸியன் அல்காரிதத்தைப் பயன்படுத்தி மெட்ரிக்குகள் ட்ரெப்சாய்டல் வடிவத்திற்குக் குறைக்கப்படுகின்றன. காஸ் அல்காரிதத்தின் யோசனை என்னவென்றால், மேட்ரிக்ஸின் முதல் வரிசையின் கூறுகளை தொடர்புடைய காரணிகளால் பெருக்குவதன் மூலம், முதல் நெடுவரிசையின் அனைத்து கூறுகளும் உறுப்புக்கு கீழே அமைந்துள்ளன.
, பூஜ்ஜியமாக மாறும். பின்னர், இரண்டாவது நெடுவரிசையின் கூறுகளை தொடர்புடைய காரணிகளால் பெருக்கி, இரண்டாவது நெடுவரிசையின் அனைத்து கூறுகளும் உறுப்புக்கு கீழே இருப்பதை உறுதிசெய்கிறோம்.
, பூஜ்ஜியமாக மாறும். பின்னர் அதே வழியில் தொடரவும்.

சிக்கல் 1.5.மேட்ரிக்ஸின் தரத்தை ட்ரெப்சாய்டல் வடிவத்திற்குக் குறைப்பதன் மூலம் தீர்மானிக்கவும்.

.

காஸியன் அல்காரிதத்தைப் பயன்படுத்துவதை எளிதாக்க, நீங்கள் முதல் மற்றும் மூன்றாவது வரிகளை மாற்றலாம்.








.

அது இங்கே தெளிவாக உள்ளது
. இருப்பினும், முடிவை மிகவும் நேர்த்தியான வடிவத்திற்கு கொண்டு வர, நீங்கள் நெடுவரிசைகளை மாற்றுவதைத் தொடரலாம்.










.

ஒரு எண் r ஆனது அணி A இன் ரேங்க் என அழைக்கப்படுகிறது:
1) அணி A இல் பூஜ்ஜியத்திலிருந்து வேறுபட்ட r வரிசையின் மைனர் உள்ளது;
2) அனைத்து மைனர்களும் (r+1) மற்றும் அதற்கு மேல் இருந்தால், அவை பூஜ்ஜியத்திற்கு சமம்.
இல்லையெனில், மேட்ரிக்ஸின் தரவரிசை பூஜ்ஜியத்தைத் தவிர மிக உயர்ந்த சிறிய வரிசையாகும்.
பதவிகள்: rangA, r A அல்லது r.
வரையறையில் இருந்து r என்பது ஒரு முழு எண் நேர்மறை எண். பூஜ்ய அணிக்கு, தரவரிசை பூஜ்ஜியமாகக் கருதப்படுகிறது.

சேவையின் நோக்கம். ஆன்லைன் கால்குலேட்டர் கண்டுபிடிக்க வடிவமைக்கப்பட்டுள்ளது அணி தரவரிசை. இந்த வழக்கில், தீர்வு வேர்ட் மற்றும் எக்செல் வடிவத்தில் சேமிக்கப்படும். உதாரண தீர்வைப் பார்க்கவும்.

வழிமுறைகள். மேட்ரிக்ஸ் பரிமாணத்தைத் தேர்ந்தெடுத்து, அடுத்து என்பதைக் கிளிக் செய்யவும்.

வரையறை . தரவரிசை r இன் அணி கொடுக்கப்பட வேண்டும். பூஜ்ஜியத்திலிருந்து வேறுபட்ட மற்றும் r வரிசையைக் கொண்ட எந்த சிறிய அணியும் அடிப்படை என்றும், அதன் கூறுகளின் வரிசைகள் மற்றும் நெடுவரிசைகள் அடிப்படை வரிசைகள் மற்றும் நெடுவரிசைகள் என்றும் அழைக்கப்படுகின்றன.
இந்த வரையறையின்படி, ஒரு அணி A பல அடிப்படை மைனர்களைக் கொண்டிருக்கலாம்.

அடையாள அணி E இன் தரவரிசை n (வரிசைகளின் எண்ணிக்கை).

எடுத்துக்காட்டு 1. இரண்டு மெட்ரிக்குகள் கொடுக்கப்பட்டால், மற்றும் அவர்களின் சிறார்களும் , . அவற்றில் எதை அடிப்படையாக எடுத்துக்கொள்ளலாம்?
தீர்வு. மைனர் M 1 =0, எனவே இது எந்த மெட்ரிக்குகளுக்கும் அடிப்படையாக இருக்க முடியாது. மைனர் M 2 =-9≠0 மற்றும் வரிசை 2 உள்ளது, அதாவது இது A அல்லது / மற்றும் B ஆகிய மெட்ரிக்குகளின் அடிப்படையாக எடுத்துக்கொள்ளப்படலாம், அவை 2 க்கு சமமான ரேங்க்களைக் கொண்டிருந்தால். detB=0 (இரண்டு விகிதாசார நெடுவரிசைகளைக் கொண்ட ஒரு தீர்மானிப்பாளராக), பின்னர் rangB=2 மற்றும் M 2 ஆகியவை அணி B இன் அடிப்படை மைனராக எடுத்துக்கொள்ளப்படலாம். அணி A இன் தரவரிசை 3 ஆகும், ஏனெனில் detA=-27≠ 0 எனவே, இந்த மேட்ரிக்ஸின் அடிப்படை மைனர் 3 க்கு சமமாக இருக்க வேண்டும், அதாவது M 2 அணி A க்கு அடிப்படை அல்ல. மேட்ரிக்ஸ் A க்கு ஒரு ஒற்றை அடிப்படை மைனர் உள்ளது, இது அணி A இன் நிர்ணயிப்பிற்கு சமம் என்பதை நினைவில் கொள்க.

தேற்றம் (சிறிய அடிப்படையைப் பற்றி). மேட்ரிக்ஸின் எந்த வரிசையும் (நெடுவரிசை) அதன் அடிப்படை வரிசைகளின் (நெடுவரிசைகள்) நேரியல் கலவையாகும்.
தேற்றத்திலிருந்து தொடர்ச்சிகள்.

1. r இன் ஒவ்வொரு (r+1) நெடுவரிசை (வரிசை) அணியும் நேரியல் சார்ந்தது.
2. அணி தரவரிசை என்றால் குறைவான எண்ணிக்கைஅதன் வரிசைகள் (நெடுவரிசைகள்), அதன் வரிசைகள் (நெடுவரிசைகள்) நேரியல் சார்ந்து இருக்கும். ரேங்க் ஏ என்றால் எண்ணுக்கு சமம்அதன் வரிசைகள் (நெடுவரிசைகள்), பின்னர் வரிசைகள் (நெடுவரிசைகள்) நேரியல் சுயாதீனமானவை.
3. ஒரு அணி A இன் நிர்ணயம் பூஜ்ஜியத்திற்கு சமம், அதன் வரிசைகள் (நெடுவரிசைகள்) நேரியல் சார்ந்து இருந்தால் மட்டுமே.
4. பூஜ்ஜியத்தைத் தவிர வேறு எந்த எண்ணாலும் பெருக்கப்படும் ஒரு அணியின் வரிசையில் (நெடுவரிசை) மற்றொரு வரிசையை (நெடுவரிசை) சேர்த்தால், அணியின் தரம் மாறாது.
5. மற்ற வரிசைகளின் (நெடுவரிசைகளின்) நேரியல் கலவையான மேட்ரிக்ஸில் ஒரு வரிசையை (நெடுவரிசை) கடந்துவிட்டால், மேட்ரிக்ஸின் தரவரிசை மாறாது.
6. மேட்ரிக்ஸின் தரவரிசை அதன் நேரியல் சார்பற்ற வரிசைகளின் (நெடுவரிசைகள்) அதிகபட்ச எண்ணிக்கைக்கு சமம்.
7. நேரியல் சார்பற்ற வரிசைகளின் அதிகபட்ச எண்ணிக்கையானது நேரியல் சார்பற்ற நெடுவரிசைகளின் அதிகபட்ச எண்ணிக்கையைப் போலவே இருக்கும்.

எடுத்துக்காட்டு 2. மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும் .
தீர்வு. மேட்ரிக்ஸ் தரவரிசையின் வரையறையின் அடிப்படையில், பூஜ்ஜியத்திலிருந்து வேறுபட்ட, உயர்ந்த வரிசையின் மைனரைத் தேடுவோம். முதலில் மேட்ரிக்ஸை மேலும் மாற்றுவோம் எளிய பார்வை. இதைச் செய்ய, மேட்ரிக்ஸின் முதல் வரிசையை (-2) பெருக்கி இரண்டாவதாகச் சேர்க்கவும், பின்னர் அதை (-1) ஆல் பெருக்கி மூன்றாவது வரிசையில் சேர்க்கவும்.

தலைப்பின் முக்கியமான நடைமுறை பயன்பாட்டையும் நாங்கள் கருத்தில் கொள்வோம்: அமைப்பு ஆராய்ச்சி நேரியல் சமன்பாடுகள்கூட்டுக்கு.

மேட்ரிக்ஸின் தரவரிசை என்ன?

கட்டுரையின் நகைச்சுவையான கல்வெட்டில் உள்ளது பெரிய பங்குஉண்மை. நாங்கள் வழக்கமாக "தரவரிசை" என்ற வார்த்தையை ஒருவித வரிசைமுறையுடன் தொடர்புபடுத்துகிறோம், பெரும்பாலும் ஒரு தொழில் ஏணியுடன். ஒருவருக்கு அறிவு, அனுபவம், திறன்கள், தொடர்புகள் போன்றவை அதிகமாக இருக்கும். - அவரது நிலை மற்றும் வாய்ப்புகளின் வரம்பு உயர்ந்தது. இளைஞர்களின் அடிப்படையில், ரேங்க் என்பது "செங்குத்தான" பொது அளவைக் குறிக்கிறது.

எங்கள் கணித சகோதரர்கள் அதே கொள்கைகளின்படி வாழ்கின்றனர். தற்செயலாக சிலவற்றை நடைப்பயிற்சிக்கு எடுத்துக்கொள்வோம் பூஜ்ஜிய மெட்ரிக்குகள்:

மேட்ரிக்ஸில் இருந்தால் அதைப் பற்றி யோசிப்போம் அனைத்து பூஜ்ஜியங்கள், அப்புறம் என்ன ரேங்க் பற்றி பேசலாம்? "மொத்த பூஜ்யம்" என்ற முறைசாரா வெளிப்பாடு அனைவருக்கும் தெரிந்ததே. மெட்ரிக்குகளின் சமூகத்தில் எல்லாம் சரியாகவே உள்ளது:

பூஜ்ஜிய மேட்ரிக்ஸின் தரவரிசைஎந்த அளவும் பூஜ்ஜியத்திற்கு சமம்.

குறிப்பு : பூஜ்ஜிய அணி "தீட்டா" என்ற கிரேக்க எழுத்தால் குறிக்கப்படுகிறது.

மேட்ரிக்ஸின் தரத்தை நன்றாகப் புரிந்துகொள்வதற்காக, இனிமேல் நான் உதவும் பொருட்களைப் பயன்படுத்துவேன் பகுப்பாய்வு வடிவியல். பூஜ்ஜியத்தைக் கவனியுங்கள் திசையன்எங்கள் முப்பரிமாண இடம், இது ஒரு குறிப்பிட்ட திசையை அமைக்காது மற்றும் கட்டிடத்திற்கு பயனற்றது இணைப்பு அடிப்படையில். இயற்கணிதக் கண்ணோட்டத்தில், இந்த வெக்டரின் ஆயத்தொலைவுகள் எழுதப்பட்டுள்ளன அணி"மூன்று ஒன்று" மற்றும் தர்க்கரீதியானது (குறிப்பிடப்பட்ட வடிவியல் அர்த்தத்தில்)இந்த மேட்ரிக்ஸின் தரவரிசை பூஜ்ஜியம் என்று வைத்துக்கொள்வோம்.

இப்போது சிலவற்றைப் பார்ப்போம் பூஜ்யம் அல்லாத நெடுவரிசை திசையன்கள்மற்றும் வரிசை திசையன்கள்:


ஒவ்வொரு நிகழ்விலும் குறைந்தது ஒரு பூஜ்ஜியம் அல்லாத உறுப்பு உள்ளது, அது ஒன்றுதான்!

பூஜ்ஜியமற்ற வரிசை வெக்டரின் (நெடுவரிசை திசையன்) ரேங்க் ஒன்றுக்கு சமம்

மற்றும் பொதுவாகச் சொன்னால் - அணியில் இருந்தால் தன்னிச்சையான அளவுகள்குறைந்தது ஒரு பூஜ்ஜியமற்ற உறுப்பு உள்ளது, பின்னர் அதன் தரவரிசை குறையாமல்அலகுகள்.

இயற்கணித வரிசை திசையன்கள் மற்றும் நெடுவரிசை திசையன்கள் ஒரு குறிப்பிட்ட அளவிற்கு சுருக்கமானவை, எனவே மீண்டும் வடிவியல் தொடர்புக்கு திரும்புவோம். பூஜ்யம் அல்லாதது திசையன்விண்வெளியில் மிகவும் திட்டவட்டமான திசையை அமைக்கிறது மற்றும் கட்டுமானத்திற்கு ஏற்றது அடிப்படையில், எனவே மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்கு சமமாக கருதப்படும்.

தத்துவார்த்த தகவல் : நேரியல் இயற்கணிதத்தில், திசையன் என்பது ஒரு திசையன் இடத்தின் ஒரு உறுப்பு (8 கோட்பாடுகள் மூலம் வரையறுக்கப்படுகிறது), இது குறிப்பாக, வரையறுக்கப்பட்ட ஒரு உண்மையான எண்ணால் கூட்டல் மற்றும் பெருக்கல் செயல்பாடுகளுடன் உண்மையான எண்களின் வரிசைப்படுத்தப்பட்ட வரிசையை (அல்லது நெடுவரிசை) குறிக்கும். அவர்களுக்காக. மேலும் விரிவான தகவல்திசையன்கள் பற்றி கட்டுரையில் காணலாம் நேரியல் மாற்றங்கள்.

நேரியல் சார்ந்தது(ஒருவருக்கொருவர் மூலம் வெளிப்படுத்தப்படுகிறது). உடன் வடிவியல் புள்ளிபார்க்க, இரண்டாவது வரியில் கோலினியர் வெக்டரின் ஆயத்தொலைவுகள் உள்ளன , இது கட்டியமைப்பதில் விஷயத்தை முன்னேற்றவில்லை முப்பரிமாண அடிப்படையில், இந்த அர்த்தத்தில் இருப்பது மிகையானது. எனவே, இந்த மேட்ரிக்ஸின் தரமும் ஒன்றுக்கு சமம்.

திசையன்களின் ஆயங்களை நெடுவரிசைகளாக மீண்டும் எழுதுவோம் ( அணியை மாற்றவும்):

ரேங்க் அடிப்படையில் என்ன மாறிவிட்டது? ஒன்றுமில்லை. நெடுவரிசைகள் விகிதாசாரமாக உள்ளன, அதாவது தரவரிசை ஒன்றுக்கு சமம். மூலம், மூன்று வரிகளும் விகிதாசாரமாக உள்ளன என்பதை நினைவில் கொள்க. அவற்றை ஆயத்தொகுப்புகளுடன் அடையாளம் காணலாம் மூன்றுவிமானத்தின் கோலினியர் திசையன்கள், இதில் ஒரே ஒருஒரு "பிளாட்" அடிப்படையை உருவாக்க பயனுள்ளதாக இருக்கும். மேலும் இது நமது வடிவியல் ரேங்க் உணர்வோடு முற்றிலும் ஒத்துப்போகிறது.

மேலே உள்ள எடுத்துக்காட்டில் இருந்து ஒரு முக்கியமான அறிக்கை பின்வருமாறு:

வரிசைகளில் உள்ள மேட்ரிக்ஸின் ரேங்க் நெடுவரிசைகளில் உள்ள மேட்ரிக்ஸின் தரத்திற்கு சமம். திறம்பட பற்றி பாடத்தில் இதை ஏற்கனவே கொஞ்சம் குறிப்பிட்டுள்ளேன் தீர்மானிப்பதைக் கணக்கிடுவதற்கான முறைகள்.

குறிப்பு : இது பின்வரும் வரிசைகளின் நேரியல் சார்பிலிருந்து நேரியல் சார்புநெடுவரிசைகள் (மற்றும் நேர்மாறாகவும்). ஆனால் நேரத்தை மிச்சப்படுத்தவும், பழக்கத்திற்கு மாறாகவும், நான் எப்போதும் சரங்களின் நேரியல் சார்பு பற்றி பேசுவேன்.

எங்கள் அன்பான செல்லப்பிராணிக்கு தொடர்ந்து பயிற்சி அளிப்போம். மூன்றாவது வரிசையில் உள்ள மேட்ரிக்ஸில் மற்றொரு கோலினியர் வெக்டரின் ஆயங்களைச் சேர்ப்போம் :

முப்பரிமாண அடிப்படையை உருவாக்க அவர் எங்களுக்கு உதவி செய்தாரா? நிச்சயமாக இல்லை. மூன்று திசையன்களும் ஒரே பாதையில் முன்னும் பின்னுமாக நடக்கின்றன, மேலும் மேட்ரிக்ஸின் தரவரிசை ஒன்றுக்கு சமம். நீங்கள் விரும்பும் பல கோலினியர் திசையன்களை நீங்கள் எடுக்கலாம், 100 என்று சொல்லுங்கள், அவற்றின் ஆயங்களை “நூறுக்கு மூன்று” மேட்ரிக்ஸில் வைக்கவும், அத்தகைய வானளாவிய கட்டிடத்தின் தரம் இன்னும் ஒன்றாகவே இருக்கும்.

மேட்ரிக்ஸைப் பற்றி அறிந்து கொள்வோம், அதன் வரிசைகள் நேரியல் சார்பற்றது. ஒரு ஜோடி அல்லாத கோலினியர் திசையன்கள் முப்பரிமாண அடிப்படையை உருவாக்க ஏற்றது. இந்த மேட்ரிக்ஸின் தரவரிசை இரண்டு.

மேட்ரிக்ஸின் தரவரிசை என்ன? கோடுகள் விகிதாசாரமாகத் தெரியவில்லை... எனவே, கோட்பாட்டில், அவை மூன்று. இருப்பினும், இந்த மேட்ரிக்ஸின் தரமும் இரண்டு. நான் முதல் இரண்டு வரிகளைச் சேர்த்து, முடிவை கீழே எழுதினேன், அதாவது. நேர்கோட்டில் வெளிப்படுத்தப்பட்டதுமுதல் இரண்டு வழியாக மூன்றாவது வரி. வடிவியல் ரீதியாக, மேட்ரிக்ஸின் வரிசைகள் மூன்றின் ஆயத்தொலைவுகளுக்கு ஒத்திருக்கும் coplanar திசையன்கள், மற்றும் இந்த மூவரில் ஒரு ஜோடி அல்லாத கோலினியர் தோழர்கள் உள்ளனர்.

நீங்கள் பார்க்க முடியும் என, நேரியல் சார்புகருதப்படும் மேட்ரிக்ஸில் வெளிப்படையாக இல்லை, இன்று அதை எவ்வாறு திறந்த வெளியில் கொண்டு வருவது என்பதைக் கற்றுக்கொள்வோம்.

மேட்ரிக்ஸின் தரவரிசை என்ன என்பதை பலர் யூகிக்க முடியும் என்று நினைக்கிறேன்!

வரிசைகளைக் கொண்ட மேட்ரிக்ஸைக் கவனியுங்கள் நேரியல் சார்பற்றது. திசையன்கள் உருவாகின்றன இணைப்பு அடிப்படையில், மற்றும் இந்த மேட்ரிக்ஸின் தரவரிசை மூன்று.

உங்களுக்கு தெரியும், முப்பரிமாண இடத்தின் எந்த நான்காவது, ஐந்தாவது, பத்தாவது திசையன் மூலம் நேர்கோட்டில் வெளிப்படுத்தப்படும் அடிப்படை திசையன்கள். எனவே, ஒரு மேட்ரிக்ஸில் ஏதேனும் வரிசைகளைச் சேர்த்தால், அதன் தரவரிசை இன்னும் மூன்று சமமாக இருக்கும்.

மெட்ரிக்குகளுக்கும் இதே போன்ற பகுத்தறிவை மேற்கொள்ளலாம் பெரிய அளவுகள்(நிச்சயமாக, எந்த வடிவியல் பொருள் இல்லாமல்).

வரையறை : மேட்ரிக்ஸின் தரவரிசை அதிகபட்ச தொகைநேரியல் சார்பற்ற வரிசைகள். அல்லது: மேட்ரிக்ஸின் தரவரிசை என்பது நேரியல் சார்பற்ற நெடுவரிசைகளின் அதிகபட்ச எண்ணிக்கையாகும். ஆம், அவர்களின் எண்ணிக்கை எப்போதும் ஒரே மாதிரியாக இருக்கும்.

மேற்கூறியவற்றிலிருந்து ஒரு முக்கியமான நடைமுறை வழிகாட்டுதலும் பின்வருமாறு: மேட்ரிக்ஸின் தரவரிசை அதன் குறைந்தபட்ச பரிமாணத்தை விட அதிகமாக இல்லை. உதாரணமாக, மேட்ரிக்ஸில் நான்கு வரிசைகள் மற்றும் ஐந்து நெடுவரிசைகள். குறைந்தபட்ச பரிமாணம் நான்கு, எனவே, இந்த மேட்ரிக்ஸின் தரவரிசை நிச்சயமாக 4 ஐ விட அதிகமாக இருக்காது.

பதவிகள்: உலகக் கோட்பாடு மற்றும் நடைமுறையில், ஒரு மேட்ரிக்ஸின் தரத்தை நியமிப்பதற்கு பொதுவாக ஏற்றுக்கொள்ளப்பட்ட தரநிலை எதுவும் இல்லை: - அவர்கள் சொல்வது போல், ஒரு ஆங்கிலேயர் ஒரு விஷயத்தை எழுதுகிறார். எனவே, அமெரிக்க மற்றும் ரஷ்ய நரகத்தைப் பற்றிய பிரபலமான நகைச்சுவையின் அடிப்படையில், மேட்ரிக்ஸின் தரத்தை ஒரு சொந்த வார்த்தையுடன் குறிப்போம். உதாரணத்திற்கு: . மேட்ரிக்ஸ் "பெயரிடப்படாதது" என்றால், அதில் பல உள்ளன, நீங்கள் வெறுமனே எழுதலாம் .

சிறார்களைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையை எவ்வாறு கண்டுபிடிப்பது?

என் பாட்டியின் மேட்ரிக்ஸில் ஐந்தாவது நெடுவரிசை இருந்தால், அவர் 4 வது வரிசையில் (“நீலம்”, “ராஸ்பெர்ரி” + 5 வது நெடுவரிசை) மற்றொரு மைனரைக் கணக்கிட வேண்டும்.

முடிவுரை: பூஜ்ஜியம் அல்லாத மைனரின் அதிகபட்ச வரிசை மூன்று, அதாவது .

ஒருவேளை எல்லோரும் இந்த சொற்றொடரை முழுமையாகப் புரிந்து கொள்ளவில்லை: 4 வது வரிசையின் மைனர் பூஜ்ஜியத்திற்கு சமம், ஆனால் 3 வது வரிசையின் சிறார்களில் பூஜ்ஜியமற்ற ஒன்று இருந்தது - எனவே அதிகபட்ச வரிசை பூஜ்யம் அல்லாதசிறிய மற்றும் சமம் மூன்று.

கேள்வி எழுகிறது: தீர்மானிப்பதை ஏன் உடனடியாக கணக்கிடக்கூடாது? சரி, முதலாவதாக, பெரும்பாலான பணிகளில் மேட்ரிக்ஸ் சதுரமாக இல்லை, இரண்டாவதாக, நீங்கள் பூஜ்ஜியமற்ற மதிப்பைப் பெற்றாலும், பணி பெரும்பாலும் நிராகரிக்கப்படும், ஏனெனில் இது வழக்கமாக நிலையான "கீழ்-மேல்" தீர்வை உள்ளடக்கியது. கருத்தில் கொள்ளப்பட்ட எடுத்துக்காட்டில், 4 வது வரிசையின் பூஜ்ஜிய நிர்ணயிப்பானது, மேட்ரிக்ஸின் தரவரிசை நான்கிற்கு குறைவாக இருப்பதைக் கூற அனுமதிக்கிறது.

நான் ஒப்புக்கொள்ள வேண்டும், சிறார்களை எல்லைக்குட்படுத்தும் முறையை சிறப்பாக விளக்குவதற்காக என்னை நானே பகுப்பாய்வு செய்த சிக்கலை நான் கொண்டு வந்தேன். நடைமுறையில், எல்லாம் எளிமையானது:

எடுத்துக்காட்டு 2

எட்ஜ் மைனர்ஸ் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

தீர்வு மற்றும் பதில் பாடத்தின் முடிவில் உள்ளது.

அல்காரிதம் எப்போது வேகமாக வேலை செய்யும்? அதே நான்கால் நான்கு அணிக்கு வருவோம். . வெளிப்படையாக, தீர்வு "நல்லது" விஷயத்தில் மிகக் குறுகியதாக இருக்கும். மூலையில் சிறார்:

மற்றும், என்றால் , பின்னர் , இல்லையெனில் – .

சிந்தனை முற்றிலும் கற்பனையானது அல்ல - முழு விஷயமும் கோண சிறார்களுக்கு மட்டுமே வரையறுக்கப்பட்ட பல எடுத்துக்காட்டுகள் உள்ளன.

இருப்பினும், சில சந்தர்ப்பங்களில் மற்றொரு முறை மிகவும் பயனுள்ளதாகவும் விரும்பத்தக்கதாகவும் இருக்கும்:

காஸியன் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரத்தை எவ்வாறு கண்டுபிடிப்பது?

பத்தி ஏற்கனவே தெரிந்த வாசகர்களுக்காக வடிவமைக்கப்பட்டுள்ளது காசியன் முறைமற்றும் அதிகமாகவோ அல்லது குறைவாகவோ தங்கள் கைகளில் கிடைத்தது.

தொழில்நுட்பக் கண்ணோட்டத்தில், முறை புதுமையானது அல்ல:

1) அடிப்படை மாற்றங்களைப் பயன்படுத்தி, மேட்ரிக்ஸை ஒரு படிநிலை வடிவத்தில் குறைக்கிறோம்;

2) மேட்ரிக்ஸின் தரவரிசை வரிசைகளின் எண்ணிக்கைக்கு சமம்.

என்பது முற்றிலும் தெளிவாக உள்ளது காஸியன் முறையைப் பயன்படுத்துவதால் மேட்ரிக்ஸின் தரம் மாறாது, மற்றும் இங்கே சாராம்சம் மிகவும் எளிமையானது: அல்காரிதம் படி, அடிப்படை மாற்றங்களின் போது, ​​அனைத்து தேவையற்ற விகிதாசார (நேரியல் சார்ந்த) வரிசைகள் அடையாளம் காணப்பட்டு அகற்றப்படுகின்றன, இதன் விளைவாக "உலர்ந்த எச்சம்" - அதிகபட்ச நேரியல் சுயாதீன வரிசைகள்.

பழைய பரிச்சயமான மேட்ரிக்ஸை மாற்றுவோம் மூன்றின் ஆயத்தொகுப்புகள்கோலினியர் திசையன்கள்:

(1) முதல் வரி இரண்டாவது வரியில் சேர்க்கப்பட்டது, பெருக்கல் –2. முதல் வரி மூன்றாவது வரியில் சேர்க்கப்பட்டது.

(2) பூஜ்ஜிய கோடுகள் அகற்றப்படும்.

எனவே, ஒரு வரி மீதமுள்ளது, எனவே . 2 வது வரிசையின் ஒன்பது பூஜ்ஜிய மைனர்களைக் கணக்கிடுவதை விட இது மிக விரைவானது என்று சொல்லத் தேவையில்லை.

அதையே உங்களுக்கு நினைவூட்டுகிறேன் இயற்கணித அணிஎதையும் மாற்ற முடியாது, மேலும் தரவரிசையை நிர்ணயிக்கும் நோக்கத்திற்காக மட்டுமே மாற்றங்கள் செய்யப்படுகின்றன! மூலம், கேள்வியில் மீண்டும் ஒருமுறை வாழ்வோம், ஏன் இல்லை? மூல அணி 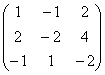அணி மற்றும் வரிசையின் தகவலிலிருந்து அடிப்படையில் வேறுபட்ட தகவலைக் கொண்டுள்ளது. சிலவற்றில் கணித மாதிரிகள்(மிகைப்படுத்தல் இல்லை) ஒரு எண்ணில் உள்ள வேறுபாடு வாழ்க்கை மற்றும் இறப்பு விஷயமாக இருக்கலாம். ... ஞாபகம் வந்தது பள்ளி ஆசிரியர்கள்ஆரம்ப மற்றும் இடைநிலை வகுப்புகளின் கணிதவியலாளர்கள், சிறிதளவு துல்லியமின்மை அல்லது அல்காரிதத்திலிருந்து விலகலுக்கு இரக்கமின்றி தரத்தை 1-2 புள்ளிகளால் குறைக்கிறார்கள். வெளித்தோற்றத்தில் உத்தரவாதம் அளிக்கப்பட்ட "A" க்கு பதிலாக, அது "நல்லது" அல்லது அதைவிட மோசமாக மாறியது மிகவும் ஏமாற்றத்தை அளித்தது. புரிதல் மிகவும் பின்னர் வந்தது - செயற்கைக்கோள்கள், அணு ஆயுதங்கள் மற்றும் மின் உற்பத்தி நிலையங்களை ஒரு நபரிடம் வேறு எப்படி ஒப்படைப்பது? ஆனால் கவலைப்பட வேண்டாம், நான் இந்த பகுதிகளில் வேலை செய்யவில்லை =)

மிகவும் அர்த்தமுள்ள பணிகளுக்குச் செல்வோம், மற்றவற்றுடன், முக்கியமான கணக்கீட்டு நுட்பங்களைப் பற்றி அறிந்து கொள்வோம். காஸ் முறை:

எடுத்துக்காட்டு 3

அடிப்படை மாற்றங்களைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

தீர்வு: ஒரு "நான்கு ஐந்து" அணி வழங்கப்படுகிறது, அதாவது அதன் தரவரிசை நிச்சயமாக 4 க்கு மேல் இல்லை.

முதல் நெடுவரிசையில், 1 அல்லது –1 இல்லை, எனவே, குறைந்தபட்சம் ஒரு யூனிட்டையாவது பெற கூடுதல் நடவடிக்கைகள் தேவை. தளத்தின் இருப்பு முழுவதும், என்னிடம் மீண்டும் மீண்டும் கேள்வி கேட்கப்பட்டது: "அடிப்படை மாற்றங்களின் போது நெடுவரிசைகளை மறுசீரமைக்க முடியுமா?" இங்கே - நாங்கள் முதல் மற்றும் இரண்டாவது நெடுவரிசைகளை மறுசீரமைத்தோம், எல்லாம் நன்றாக இருக்கிறது! இது பயன்படுத்தப்படும் பெரும்பாலான பணிகளில் காசியன் முறை, நெடுவரிசைகளை உண்மையில் மறுசீரமைக்க முடியும். ஆனால் தேவையில்லை. மேலும் புள்ளியானது மாறிகளுடன் சாத்தியமான குழப்பத்தில் கூட இல்லை, புள்ளி என்னவென்றால், உயர் கணிதத்தின் கிளாசிக்கல் போக்கில் இந்த நடவடிக்கை பாரம்பரியமாக கருதப்படுவதில்லை, எனவே அத்தகைய தலையீடு மிகவும் வக்கிரமாக பார்க்கப்படும் (அல்லது எல்லாவற்றையும் மீண்டும் செய்ய வேண்டிய கட்டாயம் கூட).

இரண்டாவது புள்ளி எண்களைப் பற்றியது. நீங்கள் உங்கள் முடிவை எடுக்கும்போது, ​​பின்வரும் கட்டைவிரல் விதியைப் பயன்படுத்துவது உதவியாக இருக்கும்: அடிப்படை மாற்றங்கள், முடிந்தால், மேட்ரிக்ஸ் எண்களைக் குறைக்க வேண்டும். எல்லாவற்றிற்கும் மேலாக, ஒன்று, இரண்டு, மூன்றுடன் வேலை செய்வது மிகவும் எளிதானது, எடுத்துக்காட்டாக, 23, 45 மற்றும் 97 ஐ விட. மேலும் முதல் செயல், முதல் நெடுவரிசையில் ஒன்றைப் பெறுவது மட்டுமல்லாமல், எண்களை நீக்குவதையும் நோக்கமாகக் கொண்டுள்ளது. 7 மற்றும் 11.

முதலில் முழுமையான தீர்வு, பின்னர் கருத்துகள்:

(1) முதல் வரி இரண்டாவது வரியில் சேர்க்கப்பட்டது, பெருக்கல் –2. முதல் வரி மூன்றாவது வரியில் சேர்க்கப்பட்டது, -3 ஆல் பெருக்கப்பட்டது. மற்றும் குவியலுக்கு: 1 வது வரி 4 வது வரியில் சேர்க்கப்பட்டது, -1 ஆல் பெருக்கப்பட்டது.

(2) கடைசி மூன்று வரிகள் விகிதாசாரமாக உள்ளன. 3 மற்றும் 4 வது வரிகள் அகற்றப்பட்டன, இரண்டாவது வரி முதல் இடத்திற்கு மாற்றப்பட்டது.

(3) முதல் வரி இரண்டாவது வரியில் சேர்க்கப்பட்டது, -3 ஆல் பெருக்கப்பட்டது.

எக்கலான் வடிவத்தில் குறைக்கப்பட்ட அணி இரண்டு வரிசைகளைக் கொண்டுள்ளது.

பதில்:

இப்போது நான்கால் நான்கு மேட்ரிக்ஸை சித்திரவதை செய்வது உங்கள் முறை:

எடுத்துக்காட்டு 4

காஸியன் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

அதை உங்களுக்கு நினைவூட்டுகிறேன் காசியன் முறைதெளிவற்ற கடினத்தன்மையைக் குறிக்கவில்லை, உங்கள் முடிவு பெரும்பாலும் எனது முடிவிலிருந்து மாறுபடும். பாடத்தின் முடிவில் ஒரு பணியின் சுருக்கமான எடுத்துக்காட்டு.

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறிய நான் எந்த முறையைப் பயன்படுத்த வேண்டும்?

நடைமுறையில், தரவரிசையைக் கண்டறிய எந்த முறையைப் பயன்படுத்த வேண்டும் என்பது பெரும்பாலும் குறிப்பிடப்படவில்லை. அத்தகைய சூழ்நிலையில், நிபந்தனை பகுப்பாய்வு செய்யப்பட வேண்டும் - சில மெட்ரிக்குகளுக்கு சிறார்களின் மூலம் தீர்க்க மிகவும் பகுத்தறிவு உள்ளது, மற்றவர்களுக்கு அடிப்படை மாற்றங்களைப் பயன்படுத்துவது மிகவும் லாபகரமானது:

எடுத்துக்காட்டு 5

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

தீர்வு: முதல் முறை எப்படியோ உடனடியாக மறைந்துவிடும் =)

சற்று அதிகமாக, மேட்ரிக்ஸின் நெடுவரிசைகளைத் தொட வேண்டாம் என்று நான் அறிவுறுத்தினேன், ஆனால் பூஜ்ஜிய நெடுவரிசை அல்லது விகிதாசார/ஒத்திசைவு நெடுவரிசைகள் இருக்கும்போது, ​​​​அதை இன்னும் வெட்டுவது மதிப்பு:

(1) ஐந்தாவது நெடுவரிசை பூஜ்ஜியமாகும், அதை மேட்ரிக்ஸிலிருந்து அகற்றவும். எனவே, மேட்ரிக்ஸின் தரவரிசை நான்குக்கு மேல் இல்லை. முதல் வரி –1 ஆல் பெருக்கப்பட்டது. இது காஸ் முறையின் மற்றொரு கையொப்ப அம்சமாகும், இது பின்வரும் செயலை இனிமையான நடையாக மாற்றுகிறது:

(2) அனைத்து வரிகளிலும், இரண்டாவது முதல், முதல் வரி சேர்க்கப்பட்டது.

(3) முதல் வரி –1 ஆல் பெருக்கப்பட்டது, மூன்றாவது வரி 2 ஆல் வகுக்கப்பட்டது, நான்காவது வரி 3 ஆல் வகுக்கப்பட்டது. இரண்டாவது வரி ஐந்தாவது வரியுடன், –1 ஆல் பெருக்கப்பட்டது.

(4) மூன்றாவது வரி ஐந்தாவது வரியில் சேர்க்கப்பட்டது, அது –2 ஆல் பெருக்கப்பட்டது.

(5) கடைசி இரண்டு வரிகள் விகிதாசாரத்தில் உள்ளன, ஐந்தாவது நீக்கப்பட்டது.

முடிவு 4 வரிகள்.

பதில்:

சுயாதீன ஆய்வுக்கான நிலையான ஐந்து மாடி கட்டிடம்:

எடுத்துக்காட்டு 6

மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

பாடத்தின் முடிவில் ஒரு சிறிய தீர்வு மற்றும் பதில்.

"மேட்ரிக்ஸ் தரவரிசை" என்ற சொற்றொடர் நடைமுறையில் அடிக்கடி காணப்படவில்லை என்பதை கவனத்தில் கொள்ள வேண்டும், மேலும் பெரும்பாலான சிக்கல்களில் நீங்கள் அதை இல்லாமல் செய்ய முடியும். ஆனால் கேள்விக்குரிய கருத்து முக்கியமாக இருக்கும் ஒரு பணி உள்ளது நடிகர், மற்றும் கட்டுரையை முடிக்க இந்த நடைமுறை பயன்பாட்டைப் பார்ப்போம்:

நிலைத்தன்மைக்கான நேரியல் சமன்பாடுகளின் அமைப்பை எவ்வாறு படிப்பது?

பெரும்பாலும், தீர்வுக்கு கூடுதலாக நேரியல் சமன்பாடுகளின் அமைப்புகள்நிபந்தனையின் படி, முதலில் பொருந்தக்கூடிய தன்மைக்காக அதை ஆய்வு செய்ய வேண்டும், அதாவது எந்தவொரு தீர்வும் உள்ளது என்பதை நிரூபிக்க வேண்டும். அத்தகைய சரிபார்ப்பில் முக்கிய பங்கு வகிக்கிறது குரோனெக்கர்-காபெல்லி தேற்றம், தேவையான வடிவத்தில் நான் உருவாக்குவேன்:

தரவரிசை என்றால் கணினி மெட்ரிக்குகள்தரத்திற்கு சமம் நீட்டிக்கப்பட்ட அணி அமைப்பு, பின்னர் அமைப்பு சீரானது, மற்றும் என்றால் கொடுக்கப்பட்ட எண்தெரியாதவர்களின் எண்ணிக்கையுடன் ஒத்துப்போகிறது, பிறகு தீர்வு தனித்துவமானது.

எனவே, பொருந்தக்கூடிய அமைப்பைப் படிக்க, சமத்துவத்தை சரிபார்க்க வேண்டியது அவசியம் , எங்கே - அமைப்பு அணி(பாடத்திலிருந்து சொற்களை நினைவில் கொள்க காஸ் முறை), ஏ - நீட்டிக்கப்பட்ட கணினி அணி(அதாவது மாறிகளின் குணகங்களைக் கொண்ட அணி + இலவச சொற்களின் நெடுவரிசை).

>>மேட்ரிக்ஸ் தரவரிசை

மேட்ரிக்ஸ் தரவரிசை

மேட்ரிக்ஸின் தரத்தை தீர்மானித்தல்

கருத்தில் கொள்வோம் செவ்வக அணி. இந்த மேட்ரிக்ஸில் நாம் தன்னிச்சையாக தேர்ந்தெடுக்கிறோம் என்றால் கேகோடுகள் மற்றும் கேநெடுவரிசைகள், பின்னர் தேர்ந்தெடுக்கப்பட்ட வரிசைகள் மற்றும் நெடுவரிசைகளின் குறுக்குவெட்டில் அமைந்துள்ள உறுப்புகள் உருவாகின்றன சதுர அணி kth வரிசை. இந்த மேட்ரிக்ஸின் தீர்மானிப்பான் அழைக்கப்படுகிறது kth வரிசையில் சிறியது matrix A. வெளிப்படையாக, matrix A ஆனது m ​​மற்றும் n எண்களில் 1 முதல் சிறியது வரை எந்த வரிசையிலும் மைனர்களைக் கொண்டுள்ளது. மேட்ரிக்ஸ் A இன் அனைத்து பூஜ்ஜியமற்ற மைனர்களிலும் ஒன்று உள்ளது குறைந்தபட்சம்ஒரு மைனர் யாருடைய வரிசை மிகப் பெரியதாக இருக்கும். கொடுக்கப்பட்ட மேட்ரிக்ஸின் பூஜ்ஜியமற்ற சிறிய ஆர்டர்களில் மிகப்பெரியது அழைக்கப்படுகிறது தரவரிசைமெட்ரிக்குகள். அணி A இன் ரேங்க் என்றால் ஆர், இதன் பொருள் அணி A பூஜ்ஜியமற்ற சிறிய வரிசையைக் கொண்டுள்ளது ஆர், ஆனால் ஒவ்வொரு மைனர் ஆர்டரை விட பெரியது ஆர், பூஜ்ஜியத்திற்கு சமம். அணி A இன் ரேங்க் r(A) ஆல் குறிக்கப்படுகிறது. வெளிப்படையாக, உறவு வைத்திருக்கிறது

சிறார்களைப் பயன்படுத்தி மேட்ரிக்ஸின் தரத்தைக் கணக்கிடுதல்

மேட்ரிக்ஸின் தரவரிசை சிறார்களை எல்லைப்படுத்தும் முறை அல்லது அடிப்படை மாற்றங்களின் முறை மூலம் கண்டறியப்படுகிறது. முதல் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கணக்கிடும்போது, ​​​​ஒருவர் குறைந்த வரிசையின் மைனர்களில் இருந்து உயர் வரிசையின் மைனர்களுக்கு மாற வேண்டும். உயர் ஒழுங்கு. பூஜ்ஜியத்திலிருந்து வேறுபட்ட அணி A இன் kth வரிசையின் மைனர் D ஏற்கனவே கண்டறியப்பட்டிருந்தால், மைனர் Dயின் எல்லையில் உள்ள (k+1) வரிசை மைனர்களுக்கு மட்டுமே கணக்கீடு தேவைப்படுகிறது, அதாவது. மைனராக அதைக் கொண்டுள்ளது. அவை அனைத்தும் பூஜ்ஜியத்திற்கு சமமாக இருந்தால், மேட்ரிக்ஸின் தரவரிசை சமமாக இருக்கும் கே.

எடுத்துக்காட்டு 1.சிறார்களை எல்லைப்படுத்தும் முறையைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

.

தீர்வு.நாங்கள் 1வது வரிசை சிறார்களுடன் தொடங்குகிறோம், அதாவது. அணி A இன் உறுப்புகளில் இருந்து, எடுத்துக்காட்டாக, முதல் வரிசை மற்றும் முதல் நெடுவரிசையில் அமைந்துள்ள ஒரு சிறிய (உறுப்பு) M 1 = 1 ஐ தேர்வு செய்வோம். இரண்டாவது வரிசை மற்றும் மூன்றாவது நெடுவரிசையின் உதவியுடன் எல்லை, பூஜ்ஜியத்திலிருந்து வேறுபட்ட சிறிய M 2 = ஐப் பெறுகிறோம். இப்போது M2 எல்லையில் உள்ள 3வது வரிசை சிறார்களுக்கு திரும்புவோம். அவற்றில் இரண்டு மட்டுமே உள்ளன (நீங்கள் இரண்டாவது அல்லது நான்காவது நெடுவரிசையைச் சேர்க்கலாம்). அவற்றைக் கணக்கிடுவோம்: = 0. எனவே, மூன்றாம் வரிசையின் அனைத்து எல்லைக் மைனர்களும் பூஜ்ஜியத்திற்கு சமமாக மாறினர். அணி A இன் தரவரிசை இரண்டு.

அடிப்படை மாற்றங்களைப் பயன்படுத்தி மேட்ரிக்ஸின் தரவரிசையைக் கணக்கிடுதல்

தொடக்கநிலைபின்வரும் மேட்ரிக்ஸ் மாற்றங்கள் அழைக்கப்படுகின்றன:

1) ஏதேனும் இரண்டு வரிசைகளின் (அல்லது நெடுவரிசைகள்) வரிசைமாற்றம்

2) ஒரு வரிசையை (அல்லது நெடுவரிசையை) பூஜ்ஜியம் அல்லாத எண்ணால் பெருக்குதல்,

3) ஒரு வரிசையில் (அல்லது நெடுவரிசை) மற்றொரு வரிசையை (அல்லது நெடுவரிசை) சேர்த்தல், ஒரு குறிப்பிட்ட எண்ணால் பெருக்கப்படுகிறது.

இரண்டு மெட்ரிக்குகள் அழைக்கப்படுகின்றன இணையான, வரையறுக்கப்பட்ட அடிப்படை மாற்றங்களைப் பயன்படுத்தி அவற்றில் ஒன்று மற்றொன்றிலிருந்து பெறப்பட்டால்.

சமமான மெட்ரிக்குகள் பொதுவாகச் சமமாக இல்லை, ஆனால் அவற்றின் ரேங்க்கள் சமமாக இருக்கும். Matrices A மற்றும் B சமமானதாக இருந்தால், அது பின்வருமாறு எழுதப்பட்டுள்ளது: A~பி.

நியமனம்மேட்ரிக்ஸ் என்பது ஒரு அணி, இதில் பிரதான மூலைவிட்டத்தின் தொடக்கத்தில் ஒரு வரிசையில் பல உள்ளன (அவற்றின் எண்ணிக்கை பூஜ்ஜியமாக இருக்கலாம்), மற்ற அனைத்து கூறுகளும் பூஜ்ஜியத்திற்கு சமம், எடுத்துக்காட்டாக,

.

வரிசைகள் மற்றும் நெடுவரிசைகளின் அடிப்படை மாற்றங்களைப் பயன்படுத்தி, எந்த மேட்ரிக்ஸையும் நியமனமாக குறைக்கலாம். ஒரு நியமன மேட்ரிக்ஸின் தரவரிசை அதன் முக்கிய மூலைவிட்டத்தில் உள்ள ஒன்றின் எண்ணிக்கைக்கு சமம்.

எடுத்துக்காட்டு 2மேட்ரிக்ஸின் தரவரிசையைக் கண்டறியவும்

A=

மற்றும் அதை நியமன வடிவத்திற்கு கொண்டு வரவும்.

தீர்வு.இரண்டாவது வரியிலிருந்து, முதல் வரியைக் கழித்து, இந்த வரிகளை மறுசீரமைக்கவும்:

.

இப்போது இரண்டாவது மற்றும் மூன்றாவது வரிகளிலிருந்து முறையே 2 மற்றும் 5 ஆல் பெருக்கப்படும் முதல் வரியைக் கழிப்போம்:

;

மூன்றாவது வரியிலிருந்து முதலில் கழிக்கவும்; நாங்கள் ஒரு அணியைப் பெறுகிறோம்

பி = ,

இது மேட்ரிக்ஸ் A க்கு சமமானதாகும், ஏனெனில் இது வரையறுக்கப்பட்ட அடிப்படை மாற்றங்களின் தொகுப்பைப் பயன்படுத்தி பெறப்படுகிறது. வெளிப்படையாக, அணி B இன் தரவரிசை 2, எனவே r(A)=2. மேட்ரிக்ஸ் B ஐ எளிதாக நியமனமாக குறைக்கலாம். முதல் நெடுவரிசையைக் கழிப்பதன் மூலம், பொருத்தமான எண்களால் பெருக்கி, அனைத்து அடுத்தடுத்தவற்றிலிருந்தும், முதல் வரிசையைத் தவிர, முதல் வரிசையின் அனைத்து உறுப்புகளையும் பூஜ்ஜியமாக மாற்றுவோம், மீதமுள்ள வரிசைகளின் கூறுகள் மாறாது. பின்னர், இரண்டாவது நெடுவரிசையைக் கழித்து, பொருத்தமான எண்களால் பெருக்கி, அடுத்தடுத்த எல்லாவற்றிலிருந்தும், இரண்டாவது வரிசையைத் தவிர, இரண்டாவது வரிசையின் அனைத்து உறுப்புகளையும் பூஜ்ஜியமாக மாற்றி, நியமன மேட்ரிக்ஸைப் பெறுகிறோம்:

.