சாய்ந்த அறிகுறிகள். செயல்பாட்டு வரைபடங்களின் அறிகுறிகள்: அவற்றின் வகைகள், தீர்வுகளின் எடுத்துக்காட்டுகள்

y = f(x) செயல்பாட்டின் வரைபடத்தின் அறிகுறி ஒரு நேர் கோடு ஆகும், இது புள்ளியில் இருந்து (x, f(x)) இந்த நேர்கோட்டிற்கான தூரம் பூஜ்ஜியமாக மாறும் பண்புகளைக் கொண்டுள்ளது. தோற்றம்.

படம் 3.10 இல். செங்குத்து, கிடைமட்ட மற்றும் சாய்ந்த அறிகுறிகளின் வரைகலை எடுத்துக்காட்டுகள் கொடுக்கப்பட்டுள்ளன.

வரைபடத்தின் அறிகுறிகளைக் கண்டறிவது பின்வரும் மூன்று கோட்பாடுகளை அடிப்படையாகக் கொண்டது.

செங்குத்து அசிம்டோட் தேற்றம். y = f(x) சார்பு x 0 புள்ளியின் ஒரு குறிப்பிட்ட சுற்றுப்புறத்தில் வரையறுக்கப்படட்டும் (இந்தப் புள்ளியைத் தவிர்த்து இருக்கலாம்) மேலும் செயல்பாட்டின் ஒருபக்க வரம்புகளில் குறைந்தபட்சம் ஒன்று முடிவிலிக்கு சமமாக இருக்கும், அதாவது. பின்னர் நேர்கோடு x = x 0 என்பது y = f(x) செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறியாகும்.

வெளிப்படையாக, x 0 புள்ளியில் செயல்பாடு தொடர்ச்சியாக இருந்தால், நேர் கோடு x = x 0 செங்குத்து அறிகுறியாக இருக்க முடியாது. . இதன் விளைவாக, செயல்பாட்டின் இடைநிறுத்தப் புள்ளிகளிலோ அல்லது அதன் வரையறையின் முனைகளிலோ செங்குத்து அறிகுறிகளை தேட வேண்டும்.

கிடைமட்ட அசிம்ப்டோட் தேற்றம். y = f(x) சார்பு, போதுமான அளவு பெரிய x க்கு வரையறுக்கப்பட்டு இருக்கட்டும் இறுதி வரம்புசெயல்பாடுகள் பின்னர் வரி y = b என்பது செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

கருத்து. வரம்புகளில் ஒன்று மட்டுமே வரையறுக்கப்பட்டதாக இருந்தால், செயல்பாடு முறையே இடது பக்க அல்லது வலது பக்க கிடைமட்ட அறிகுறியைக் கொண்டுள்ளது.

அந்த நிகழ்வில், செயல்பாடு ஒரு சாய்ந்த அறிகுறியைக் கொண்டிருக்கலாம்.

சாய்ந்த அசிம்ப்டோட் தேற்றம். y = f(x) சார்பு போதுமான அளவு பெரிய x க்கு வரையறுக்கப்பட்டு வரையறுக்கப்பட்ட வரம்புகள் இருக்கட்டும் . பின்னர் நேர்கோடு y = kx + b என்பது செயல்பாட்டின் வரைபடத்தின் சாய்ந்த அறிகுறியாகும்.

ஆதாரம் இல்லை.

ஒரு கிடைமட்ட அறிகுறியைப் போலவே சாய்ந்த அறிகுறியும் வலது அல்லது இடது கையாக இருக்கலாம், தொடர்புடைய வரம்புகளின் அடிப்படையானது ஒரு குறிப்பிட்ட அடையாளத்தின் முடிவிலியாக இருந்தால்.

செயல்பாடுகளைப் படிப்பது மற்றும் அவற்றின் வரைபடங்களை உருவாக்குவது பொதுவாக பின்வரும் படிகளை உள்ளடக்கியது:

1. செயல்பாட்டின் வரையறையின் டொமைனைக் கண்டறியவும்.

2. சம-ஒற்றின்மைக்கான செயல்பாட்டை ஆராயவும்.

3. வரையறையின் களத்தின் எல்லையில் உள்ள இடைநிறுத்தப் புள்ளிகள் மற்றும் செயல்பாட்டின் நடத்தை ஆகியவற்றை ஆய்வு செய்வதன் மூலம் செங்குத்து அறிகுறிகளைக் கண்டறியவும், அவை வரையறுக்கப்பட்டதாக இருந்தால்.

4. முடிவிலியில் செயல்பாட்டின் நடத்தையை ஆராய்வதன் மூலம் கிடைமட்ட அல்லது சாய்ந்த அறிகுறிகளைக் கண்டறியவும்.

5. செயல்பாட்டின் மோனோடோனிசிட்டியின் தீவிரம் மற்றும் இடைவெளிகளைக் கண்டறியவும்.

6. செயல்பாடு மற்றும் ஊடுருவல் புள்ளிகளின் குவிவு இடைவெளிகளைக் கண்டறியவும்.

7. ஒருங்கிணைப்பு அச்சுகளுடன் வெட்டும் புள்ளிகளைக் கண்டறியவும் மற்றும் வரைபடத்தை தெளிவுபடுத்தும் சில கூடுதல் புள்ளிகளைக் கண்டறியவும்.

செயல்பாடு வேறுபாடு

ஒரு சார்பு சில அடிப்படைக்கு வரையறுக்கப்பட்ட எண்ணுக்கு சமமான வரம்பைக் கொண்டிருந்தால், அதை இந்த எண்ணின் கூட்டுத்தொகையாகவும், எண்ணற்றதாகவும் குறிப்பிடலாம். சிறிய அளவுஅதே அடித்தளத்துடன் (மற்றும் நேர்மாறாகவும்): .

இந்த தேற்றத்தை வேறுபடுத்தக்கூடிய செயல்பாட்டிற்குப் பயன்படுத்துவோம்: .

எனவே, Dу செயல்பாட்டின் அதிகரிப்பு இரண்டு சொற்களைக் கொண்டுள்ளது: 1) Dх ஐப் பொறுத்தவரை நேரியல், அதாவது. f `(x)Dх; 2) Dx ஐப் பொறுத்தவரை நேரியல் அல்ல, அதாவது. a(Dx)Dx. அதே நேரத்தில், இருந்து , இந்த இரண்டாவது காலமானது ஒரு எண்ணற்ற சிறிய அளவைக் குறிக்கிறது உயர் ஒழுங்கு Dx ஐ விட (Dx பூஜ்ஜியத்தை நோக்கி செல்வதால், அது இன்னும் வேகமாக பூஜ்ஜியமாக மாறும்).

ஒரு செயல்பாட்டின் வேறுபாடு முக்கிய, நேரியல் சார்புடைய செயல்பாட்டின் அதிகரிப்பின் Dx பகுதியாகும், இது வழித்தோன்றலின் பெருக்கத்திற்கும் dy = f `(x)Dx இன் இன்கிரிமென்ட்டுக்கும் சமமாகும்.

y = x செயல்பாட்டின் வேறுபாட்டைக் கண்டுபிடிப்போம்.

dy = f `(x)Dх = x`Dх = Dх என்பதால், dx = Dх, அதாவது. ஒரு சுயாதீன மாறியின் வேறுபாடு இந்த மாறியின் அதிகரிப்புக்கு சமம்.

எனவே, ஒரு செயல்பாட்டின் வேறுபாட்டிற்கான சூத்திரத்தை dy = f `(x)dх என எழுதலாம். அதனால்தான் வழித்தோன்றலுக்கான குறியீடுகளில் ஒன்று dy/dх என்ற பின்னம் ஆகும்.

வேற்றுமையின் வடிவியல் பொருள் விளக்கப்பட்டுள்ளது
படம் 3.11. y = f(x) செயல்பாட்டின் வரைபடத்தில் ஒரு தன்னிச்சையான புள்ளி M(x, y) ஐ எடுத்துக் கொள்வோம். வாதம் x ஐ அதிகரிப்பு Dx ஐ வழங்குவோம். பின்னர் y = f(x) சார்பு Dy = f(x + Dx) - f(x) என்ற அதிகரிப்பைப் பெறும். புள்ளி M இல் உள்ள செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு வரைவோம், இது abscissa அச்சின் நேர்மறையான திசையுடன் ஒரு கோணத்தை உருவாக்குகிறது, அதாவது. f `(x) = டான் a. வலது முக்கோணத்திலிருந்து எம்.கே.என்
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.

எனவே, ஒரு சார்பின் வேறுபாடு என்பது, x அதிகரிப்பு Dx ஐப் பெறும் போது, ​​கொடுக்கப்பட்ட புள்ளியில் சார்பின் வரைபடத்திற்கு வரையப்பட்ட தொடுகோட்டின் ஆர்டினேட்டில் உள்ள அதிகரிப்பு ஆகும்.

வேறுபாட்டின் பண்புகள் அடிப்படையில் ஒரு வழித்தோன்றலின் பண்புகளைப் போலவே இருக்கும்:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2.

இருப்பினும், ஒரு செயல்பாட்டின் வேறுபாட்டின் ஒரு முக்கியமான பண்பு உள்ளது, அதன் வழித்தோன்றல் இல்லை - இது வேறுபாட்டின் வடிவத்தின் மாறுபாடு ஆகும்.

y = f(x) செயல்பாட்டிற்கான வேறுபாட்டின் வரையறையிலிருந்து, வேறுபாடு dy = f `(x)dх. இந்த செயல்பாடு y சிக்கலானதாக இருந்தால், அதாவது. y = f(u), u = j(x), பின்னர் y = f மற்றும் f `(x) = f `(u)*u`. பிறகு dy = f `(u)*u`dх. ஆனால் விழாவிற்கு
u = j(x) வேறுபாடு du = u`dх. எனவே dy = f `(u)*du.

dy = f `(x)dх மற்றும் dy = f `(u)*du ஆகிய சமத்துவங்களை ஒப்பிட்டு, சார்பற்ற மாறியின் சார்புக்கு பதிலாக x இன் செயல்பாட்டைக் கருத்தில் கொண்டால், வேறுபட்ட சூத்திரம் மாறாது என்பதை உறுதிசெய்கிறோம். சார்பு மாறி u. வேற்றுமையின் இந்தப் பண்பு மாறுபாட்டின் வடிவத்தின் (அல்லது சூத்திரம்) மாறாத தன்மை (அதாவது, மாறாத தன்மை) எனப்படும்.

இருப்பினும், இந்த இரண்டு சூத்திரங்களில் இன்னும் வேறுபாடு உள்ளது: அவற்றில் முதலாவது, சுயாதீன மாறியின் வேறுபாடு இந்த மாறியின் அதிகரிப்புக்கு சமம், அதாவது. dx = Dx, மற்றும் இரண்டாவதாக, du செயல்பாட்டின் வேறுபாடு Du இந்த செயல்பாட்டின் அதிகரிப்பின் நேரியல் பகுதி மற்றும் சிறிய Dx du » Du க்கு மட்டுமே.

எப்படி செருகுவது கணித சூத்திரங்கள்தளத்திற்கு?

நீங்கள் எப்போதாவது ஒரு வலைப்பக்கத்தில் ஒன்று அல்லது இரண்டு கணித சூத்திரங்களைச் சேர்க்க வேண்டும் என்றால், கட்டுரையில் விவரிக்கப்பட்டுள்ளபடி இதைச் செய்வதற்கான எளிதான வழி: வொல்ஃப்ராம் ஆல்பாவால் தானாக உருவாக்கப்படும் படங்களின் வடிவத்தில் கணித சூத்திரங்கள் தளத்தில் எளிதாகச் செருகப்படுகின்றன. . எளிமை தவிர, இது உலகளாவிய முறைஇணையதளத் தெரிவுநிலையை மேம்படுத்த உதவும் தேடுபொறிகள். இது நீண்ட காலமாக வேலை செய்கிறது (மற்றும், எப்போதும் வேலை செய்யும் என்று நான் நினைக்கிறேன்), ஆனால் ஏற்கனவே தார்மீக ரீதியாக காலாவதியானது.

உங்கள் தளத்தில் நீங்கள் தொடர்ந்து கணித சூத்திரங்களைப் பயன்படுத்தினால், நீங்கள் MathJax ஐப் பயன்படுத்த பரிந்துரைக்கிறேன் - ஒரு சிறப்பு JavaScript நூலகம் கணிதக் குறியீடுஇணைய உலாவிகளில் MathML, LaTeX அல்லது ASCIIMathML மார்க்அப்பைப் பயன்படுத்துகிறது.

MathJax ஐப் பயன்படுத்தத் தொடங்குவதற்கு இரண்டு வழிகள் உள்ளன: (1) எளிய குறியீட்டைப் பயன்படுத்தி, உங்கள் வலைத்தளத்துடன் MathJax ஸ்கிரிப்டை விரைவாக இணைக்கலாம், இது சரியான நேரத்தில் தொலை சேவையகத்திலிருந்து தானாகவே ஏற்றப்படும் (சேவையகங்களின் பட்டியல்); (2) MathJax ஸ்கிரிப்டை ரிமோட் சர்வரில் இருந்து உங்கள் சர்வரில் பதிவிறக்கம் செய்து உங்கள் தளத்தின் அனைத்து பக்கங்களிலும் இணைக்கவும். இரண்டாவது முறை - மிகவும் சிக்கலானது மற்றும் நேரத்தைச் செலவழிக்கும் - உங்கள் தளத்தின் பக்கங்களை ஏற்றுவதை விரைவுபடுத்தும், மேலும் சில காரணங்களால் பெற்றோர் MathJax சேவையகம் தற்காலிகமாக கிடைக்காமல் போனால், இது உங்கள் சொந்த தளத்தை எந்த வகையிலும் பாதிக்காது. இந்த நன்மைகள் இருந்தபோதிலும், நான் முதல் முறையைத் தேர்ந்தெடுத்தேன், ஏனெனில் இது எளிமையானது, வேகமானது மற்றும் தொழில்நுட்ப திறன்கள் தேவையில்லை. எனது உதாரணத்தைப் பின்பற்றவும், மேலும் 5 நிமிடங்களில் உங்கள் தளத்தில் MathJax இன் அனைத்து அம்சங்களையும் நீங்கள் பயன்படுத்த முடியும்.

பிரதான MathJax இணையதளம் அல்லது ஆவணப் பக்கத்தில் எடுக்கப்பட்ட இரண்டு குறியீடு விருப்பங்களைப் பயன்படுத்தி தொலை சேவையகத்திலிருந்து MathJax நூலக ஸ்கிரிப்டை இணைக்கலாம்:

இந்த குறியீடு விருப்பங்களில் ஒன்றை நகலெடுத்து உங்கள் வலைப்பக்கத்தின் குறியீட்டில் ஒட்ட வேண்டும், முன்னுரிமை குறிச்சொற்களுக்கு இடையில் அல்லது குறிச்சொல்லுக்குப் பிறகு உடனடியாக. முதல் விருப்பத்தின்படி, MathJax வேகமாக ஏற்றுகிறது மற்றும் பக்கத்தின் வேகத்தை குறைக்கிறது. ஆனால் இரண்டாவது விருப்பம் MathJax இன் சமீபத்திய பதிப்புகளை தானாகவே கண்காணித்து ஏற்றுகிறது. நீங்கள் முதல் குறியீட்டைச் செருகினால், அது அவ்வப்போது புதுப்பிக்கப்பட வேண்டும். நீங்கள் இரண்டாவது குறியீட்டைச் செருகினால், பக்கங்கள் மெதுவாக ஏற்றப்படும், ஆனால் நீங்கள் தொடர்ந்து MathJax புதுப்பிப்புகளை கண்காணிக்க வேண்டியதில்லை.

MathJax ஐ இணைப்பது Blogger அல்லது WordPress இல் உள்ளது. டெம்ப்ளேட்டின் தொடக்கத்தில் (மேத்ஜாக்ஸ் ஸ்கிரிப்ட் ஒத்திசைவற்ற முறையில் ஏற்றப்பட்டதால், இது அவசியமில்லை). அவ்வளவுதான். இப்போது MathML, LaTeX மற்றும் ASCIIMathML ஆகியவற்றின் மார்க்அப் தொடரியல் கற்றுக்கொள்ளுங்கள், மேலும் உங்கள் தளத்தின் இணையப் பக்கங்களில் கணித சூத்திரங்களைச் செருக நீங்கள் தயாராக உள்ளீர்கள்.

எந்த பின்னமும் படி கட்டப்பட்டது ஒரு குறிப்பிட்ட விதி, இது வரம்பற்ற முறை தொடர்ச்சியாகப் பயன்படுத்தப்படுகிறது. அத்தகைய ஒவ்வொரு நேரமும் மறு செய்கை என்று அழைக்கப்படுகிறது.

மெங்கர் கடற்பாசியை உருவாக்குவதற்கான செயல்பாட்டு வழிமுறை மிகவும் எளிமையானது: பக்க 1 உடன் அசல் கனசதுரம் அதன் முகங்களுக்கு இணையான விமானங்களால் 27 சம கனசதுரங்களாக பிரிக்கப்பட்டுள்ளது. ஒரு மைய கனசதுரமும், முகங்களுடன் ஒட்டிய 6 கனசதுரங்களும் அதிலிருந்து அகற்றப்படுகின்றன. இதன் விளைவாக மீதமுள்ள 20 சிறிய க்யூப்ஸ் கொண்ட ஒரு தொகுப்பு ஆகும். இந்த க்யூப்ஸ் ஒவ்வொன்றிலும் இதைச் செய்தால், 400 சிறிய கனசதுரங்களைக் கொண்ட ஒரு தொகுப்பைப் பெறுகிறோம். இந்த செயல்முறையை முடிவில்லாமல் தொடர்ந்தால், நாம் ஒரு மெங்கர் கடற்பாசி கிடைக்கும்.

ஒரு ஹைபர்போலா என்பது புள்ளிகளின் இருப்பிடமாகும், அதன் இரண்டு கொடுக்கப்பட்ட புள்ளிகளுக்கான தூரத்தில் உள்ள வேறுபாடு foci என்று அழைக்கப்படுகிறது, இது ஒரு நிலையான மதிப்பு (இந்த மாறிலி நேர்மறை மற்றும் foci இடையே உள்ள தூரத்தை விட குறைவாக இருக்க வேண்டும்).

இந்த மாறிலியை 2a ஆல் குறிப்போம், foci க்கு இடையே உள்ள தூரம் மற்றும் § 3 இல் உள்ள அதே வழியில் ஒருங்கிணைப்பு அச்சுகளைத் தேர்வு செய்வோம். ஹைப்பர்போலாவின் தன்னிச்சையான புள்ளியாக இருக்கட்டும்.

ஹைப்பர்போலாவின் வரையறையின்படி

சமத்துவத்தின் வலது பக்கத்தில் நீங்கள் ஒரு கூட்டல் குறி என்றால் மற்றும் ஒரு மைனஸ் அடையாளத்தைத் தேர்ந்தெடுக்க வேண்டும்

கடைசி சமத்துவத்தை இவ்வாறு எழுதலாம்:

தேர்ந்தெடுக்கப்பட்ட ஒருங்கிணைப்பு அமைப்பில் உள்ள ஹைப்பர்போலாவின் சமன்பாடு இதுவாகும்.

இந்த சமன்பாட்டில் உள்ள தீவிரவாதிகளிடமிருந்து நம்மை விடுவித்துக் கொள்வதன் மூலம் (§ 3 இல் உள்ளதைப் போல), சமன்பாட்டை அதன் எளிய வடிவத்திற்கு குறைக்கலாம்.

முதல் ரேடிக்கலை சமத்துவத்தின் வலது பக்கத்திற்கு மாற்றுவது மற்றும் இரு பக்கங்களையும் ஸ்கொயர் செய்வது, வெளிப்படையான மாற்றங்களுக்குப் பிறகு நாம் பெறுகிறோம்:

சமத்துவத்தின் இரு பக்கங்களையும் மீண்டும் ஒருமுறை ஸ்கொயர் செய்து, ஒரே மாதிரியான விதிமுறைகளைக் கொண்டு வந்து, இலவச காலத்தால் வகுத்தால், நாம் பெறுகிறோம்:

இருந்து, மதிப்பு நேர்மறை. மூலம் அதைக் குறிக்கிறது, அதாவது, அனுமானம்

நாம் பெறுகிறோம் நியமன சமன்பாடுமிகைப்படுத்தல்.

ஹைப்பர்போலாவின் வடிவத்தை ஆராய்வோம்.

1) ஹைப்பர்போலாவின் சமச்சீர்நிலைகள். சமன்பாடு (3) தற்போதைய ஆயங்களின் சதுரங்களை மட்டுமே கொண்டிருப்பதால், ஆய அச்சுகள் ஹைப்பர்போலாவின் சமச்சீர் அச்சுகளாகும் (நீள்வட்டத்திற்கான ஒத்த அறிக்கையைப் பார்க்கவும்). குவியங்கள் அமைந்துள்ள ஹைப்பர்போலாவின் சமச்சீர் அச்சு குவிய அச்சு என்று அழைக்கப்படுகிறது. சமச்சீர் அச்சுகள் வெட்டும் புள்ளி - சமச்சீர் மையம் - ஹைபர்போலாவின் மையம் என்று அழைக்கப்படுகிறது. சமன்பாடு (3) மூலம் கொடுக்கப்பட்ட ஹைபர்போலாவிற்கு, குவிய அச்சு எருது அச்சுடன் ஒத்துப்போகிறது, மேலும் மையம்தான் தோற்றம்.

2) சமச்சீர் அச்சுகளுடன் வெட்டும் புள்ளிகள். சமச்சீர் அச்சுகளுடன் ஹைப்பர்போலாவின் குறுக்குவெட்டு புள்ளிகளைக் கண்டுபிடிப்போம் - ஹைபர்போலாவின் முனைகள். சமன்பாட்டில் அனுமானித்து, அச்சுடன் ஹைப்பர்போலாவின் வெட்டும் புள்ளிகளின் அப்சிசாஸைக் காண்கிறோம்.

இதன் விளைவாக, புள்ளிகள் ஹைபர்போலாவின் முனைகளாகும் (படம் 51); அவற்றுக்கிடையேயான தூரம் 2a ஆகும். Oy அச்சுடன் வெட்டும் புள்ளிகளைக் கண்டறிய, இந்த புள்ளிகளின் ஆர்டினேட்டுகளைத் தீர்மானிக்க, சமன்பாட்டைப் பெறுகிறோம்

அதாவது, y க்கு நாம் கற்பனை மதிப்புகளைப் பெற்றோம்; இதன் பொருள் ஓய் அச்சு ஹைப்பர்போலஸை வெட்டுவதில்லை.

இதற்கு இணங்க, ஹைப்பர்போலாவைக் குறுக்கிடும் சமச்சீர் அச்சு உண்மையான சமச்சீர் அச்சு (ஃபோகல் அச்சு) என்றும், ஹைப்பர்போலாவைக் குறுக்கிடாத சமச்சீர் அச்சு சமச்சீரின் கற்பனை அச்சு என்றும் அழைக்கப்படுகிறது. சமன்பாடு (3) மூலம் கொடுக்கப்பட்ட ஒரு ஹைபர்போலாவிற்கு, சமச்சீரின் உண்மையான அச்சு அச்சு, சமச்சீரின் கற்பனை அச்சு என்பது ஹைப்பர்போலாவின் செங்குத்துகளை இணைக்கும் அச்சு மற்றும் அதன் நீளம் 2a, உண்மையான அச்சு என்று அழைக்கப்படுகிறது. ஹைபர்போலா. ஹைப்பர்போலாவின் சமச்சீரின் கற்பனை அச்சில் அதன் மையமான O வின் இருபுறமும் OB மற்றும் நீளம் b ஆகிய பிரிவுகளை நாம் அமைத்தால், பிரிவு மற்றும் அதன் நீளம் ஹைப்பர்போலாவின் கற்பனை அச்சு எனப்படும். a மற்றும் b அளவுகள் முறையே ஹைபர்போலாவின் உண்மையான மற்றும் கற்பனை அரை அச்சுகள் என்று அழைக்கப்படுகின்றன.

3) மிகைப்படுத்தலின் வடிவம். ஹைப்பர்போலாவின் வடிவத்தைப் படிக்கும் போது, ​​x மற்றும் y இன் நேர்மறை மதிப்புகளைக் கருத்தில் கொள்வது போதுமானது, ஏனெனில் வளைவு ஒருங்கிணைப்பு அச்சுகளுடன் ஒப்பிடும்போது சமச்சீராக அமைந்துள்ளது.

சமன்பாடு (3) இலிருந்து 1 ஐப் பின்தொடர்வதால், a லிருந்து a லிருந்து a க்கு அதிகரிக்கும் போது Y ஆனது 0 லிருந்து 0 க்கு அதிகரிக்கும் வளைவு படம். 51. இது நேர் கோடுகளால் வரையறுக்கப்பட்ட துண்டுக்கு வெளியே அமைந்துள்ளது மற்றும் இரண்டு தனித்தனி கிளைகளைக் கொண்டுள்ளது. இந்தக் கிளைகளில் ஒன்றின் எந்தப் புள்ளி M க்கும் (வலது கிளை), மற்றொரு கிளையின் எந்தப் புள்ளிக்கும் M (இடது கிளை).

4) ஹைபர்போலாவின் அறிகுறிகள். ஹைப்பர்போலாவின் வகையை இன்னும் தெளிவாகக் கற்பனை செய்ய, அதனுடன் நெருங்கிய தொடர்புடைய இரண்டு நேர்கோடுகளைக் கவனியுங்கள் - அசிம்ப்டோட்கள் என்று அழைக்கப்படுபவை.

x மற்றும் y நேர்மறை எனக் கருதி, ஆர்டினேட் y ஐப் பொறுத்து ஹைப்பர்போலாவின் சமன்பாட்டை (3) தீர்க்கிறோம்:

சமன்பாட்டை ஒரு நேர் கோட்டின் சமன்பாட்டுடன் ஒப்பிடுவோம், இந்த நேர்கோட்டில் மற்றும் ஹைப்பர்போலாவில் முறையே அமைந்துள்ள தொடர்புடைய இரண்டு புள்ளிகளை அழைப்போம் மற்றும் அதே அப்சிஸ்ஸா (படம் 51). வெளிப்படையாக, தொடர்புடைய புள்ளிகளின் ஆர்டினேட்டுகளின் Y - y வேறுபாடு அவற்றுக்கிடையேயான தூரத்தை வெளிப்படுத்துகிறது, அதாவது.

வரம்பற்ற அதிகரிப்புடன், தூரம் MN, கொலை, பூஜ்ஜியமாக இருக்கும் என்பதைக் காட்டுவோம். உண்மையில்,

எளிமைப்படுத்திய பிறகு நாம் பெறுகிறோம்:

கடைசி சூத்திரத்திலிருந்து, அப்சிசாவில் வரம்பற்ற அதிகரிப்புடன், தூரம் MN குறைந்து பூஜ்ஜியமாக மாறுவதைக் காண்கிறோம். புள்ளி M, முதல் நாற்கரத்தில் ஹைபர்போலாவுடன் நகரும் போது, ​​முடிவிலிக்கு நகரும் போது, ​​அதன் நேர்கோட்டிற்கான தூரம் குறைந்து பூஜ்ஜியமாக மாறும். மூன்றாவது நாற்கரத்தில் ஒரு ஹைபர்போலாவுடன் புள்ளி M நகரும் போது இதே சூழ்நிலை ஏற்படும் (தோற்றம் O உடன் சமச்சீர் காரணமாக).

இறுதியாக, ஓய் அச்சுடன் தொடர்புடைய ஹைப்பர்போலாவின் சமச்சீர்மையின் காரணமாக, நேர்கோட்டுடன் சமச்சீராக அமைந்திருக்கும் இரண்டாவது நேர்கோட்டைப் பெறுவோம், அது ஹைப்பர்போலாவோடு நகர்ந்து முடிவிலிக்கு நகரும்போது M காலவரையின்றி அணுகும். இரண்டாவது மற்றும் நான்காவது quadrants).

இந்த இரண்டு நேர்க்கோடுகள் ஹைப்பர்போலாவின் அசிம்ப்டோட்கள் என்று அழைக்கப்படுகின்றன, மேலும் நாம் பார்த்தபடி, அவை சமன்பாடுகளைக் கொண்டுள்ளன:

வெளிப்படையாக, ஹைப்பர்போலாவின் அறிகுறிகள் ஒரு செவ்வகத்தின் மூலைவிட்டங்களில் அமைந்துள்ளன, அதன் ஒரு பக்கம் எருது அச்சுக்கு இணையாகவும் 2a க்கு சமமாகவும் உள்ளது, மற்றொன்று Oy அச்சுக்கு இணையாக உள்ளது மற்றும் மையமானது ஒருங்கிணைப்புகளின் தோற்றம் (படம் 51 ஐப் பார்க்கவும்).

அதன் சமன்பாட்டைப் பயன்படுத்தி ஒரு ஹைபர்போலாவை வரையும்போது, ​​முதலில் அதன் அறிகுறிகளை உருவாக்க பரிந்துரைக்கப்படுகிறது.

சமபக்க ஹைபர்போலா. ஒரு ஹைபர்போலா விஷயத்தில் அது சமபக்கமாக அழைக்கப்படுகிறது; அதன் சமன்பாடு (3) இலிருந்து பெறப்பட்டது மற்றும் வடிவம் உள்ளது:

வெளிப்படையாக, ஒரு சமபக்க அதிபரவளைவுக்கான அறிகுறிகளின் கோணக் குணகங்கள் அதன் விளைவாக இருக்கும், சமபக்க ஹைப்பர்போலாவின் அறிகுறிகள் ஒன்றுக்கொன்று செங்குத்தாக இருக்கும் மற்றும் அதன் சமச்சீர் அச்சுகளுக்கு இடையே உள்ள கோணங்களை இரண்டாகப் பிரிக்கின்றன.

y = f(x) செயல்பாட்டின் வரைபடத்தின் அறிகுறி ஒரு நேர் கோடு ஆகும், இது புள்ளியில் இருந்து (x, f(x)) இந்த நேர்கோட்டிற்கான தூரம் பூஜ்ஜியமாக மாறும் பண்புகளைக் கொண்டுள்ளது. தோற்றம்.

படம் 3.10 இல். செங்குத்து, கிடைமட்ட மற்றும் சாய்ந்த அறிகுறிகளின் வரைகலை எடுத்துக்காட்டுகள் கொடுக்கப்பட்டுள்ளன.

வரைபடத்தின் அறிகுறிகளைக் கண்டறிவது பின்வரும் மூன்று கோட்பாடுகளை அடிப்படையாகக் கொண்டது.

செங்குத்து அசிம்டோட் தேற்றம். y = f(x) சார்பு x 0 புள்ளியின் ஒரு குறிப்பிட்ட சுற்றுப்புறத்தில் வரையறுக்கப்படட்டும் (இந்தப் புள்ளியைத் தவிர்த்து இருக்கலாம்) மேலும் செயல்பாட்டின் ஒருபக்க வரம்புகளில் குறைந்தபட்சம் ஒன்று முடிவிலிக்கு சமமாக இருக்கும், அதாவது. பின்னர் நேர்கோடு x = x 0 என்பது y = f(x) செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறியாகும்.

வெளிப்படையாக, x 0 புள்ளியில் செயல்பாடு தொடர்ச்சியாக இருந்தால், நேர் கோடு x = x 0 செங்குத்து அறிகுறியாக இருக்க முடியாது. . இதன் விளைவாக, செயல்பாட்டின் இடைநிறுத்தப் புள்ளிகளிலோ அல்லது அதன் வரையறையின் முனைகளிலோ செங்குத்து அறிகுறிகளை தேட வேண்டும்.

கிடைமட்ட அசிம்ப்டோட் தேற்றம். y = f(x) சார்பு போதுமான அளவு பெரிய x க்கு வரையறுக்கப்படட்டும் மற்றும் செயல்பாட்டின் வரையறுக்கப்பட்ட வரம்பு உள்ளது. பின்னர் வரி y = b என்பது செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

கருத்து. வரம்புகளில் ஒன்று மட்டுமே வரையறுக்கப்பட்டதாக இருந்தால், செயல்பாடு முறையே இடது பக்க அல்லது வலது பக்க கிடைமட்ட அறிகுறியைக் கொண்டுள்ளது.

அந்த நிகழ்வில், செயல்பாடு ஒரு சாய்ந்த அறிகுறியைக் கொண்டிருக்கலாம்.

சாய்ந்த அசிம்ப்டோட் தேற்றம். y = f(x) சார்பு போதுமான அளவு பெரிய x க்கு வரையறுக்கப்பட்டு வரையறுக்கப்பட்ட வரம்புகள் இருக்கட்டும் . பின்னர் நேர்கோடு y = kx + b என்பது செயல்பாட்டின் வரைபடத்தின் சாய்ந்த அறிகுறியாகும்.

ஆதாரம் இல்லை.

ஒரு கிடைமட்ட அறிகுறியைப் போலவே சாய்ந்த அறிகுறியும் வலது அல்லது இடது கையாக இருக்கலாம், தொடர்புடைய வரம்புகளின் அடிப்படையானது ஒரு குறிப்பிட்ட அடையாளத்தின் முடிவிலியாக இருந்தால்.

செயல்பாடுகளைப் படிப்பது மற்றும் அவற்றின் வரைபடங்களை உருவாக்குவது பொதுவாக பின்வரும் படிகளை உள்ளடக்கியது:

1. செயல்பாட்டின் வரையறையின் டொமைனைக் கண்டறியவும்.

2. சம-ஒற்றின்மைக்கான செயல்பாட்டை ஆராயவும்.

3. வரையறையின் களத்தின் எல்லையில் உள்ள இடைநிறுத்தப் புள்ளிகள் மற்றும் செயல்பாட்டின் நடத்தை ஆகியவற்றை ஆய்வு செய்வதன் மூலம் செங்குத்து அறிகுறிகளைக் கண்டறியவும், அவை வரையறுக்கப்பட்டதாக இருந்தால்.

4. முடிவிலியில் செயல்பாட்டின் நடத்தையை ஆராய்வதன் மூலம் கிடைமட்ட அல்லது சாய்ந்த அறிகுறிகளைக் கண்டறியவும்.

ஒரு அசிம்டோட்டின் பேய் நீண்ட காலமாக தளத்தில் சுற்றித் திரிந்து, இறுதியாக ஒரு தனி கட்டுரையில் வெளிவருகிறது மற்றும் செயல்பாட்டைப் பற்றிய முழுமையான ஆய்வு மூலம் குழப்பமடைந்த வாசகர்களுக்கு குறிப்பிட்ட மகிழ்ச்சியைத் தருகிறது. வரைபடத்தின் அறிகுறிகளைக் கண்டறிவது, குறிப்பிட்ட பணியின் சில பகுதிகளில் ஒன்றாகும், இது பள்ளி பாடத்திட்டத்தில் மேலோட்டப் பார்வையில் மட்டுமே உள்ளது, ஏனெனில் நிகழ்வுகள் செயல்பாடுகளின் வரம்புகளைக் கணக்கிடுவதைச் சுற்றி வருகின்றன, மேலும் அவை இன்னும் உயர் கணிதத்துடன் தொடர்புடையவை. கணிதப் பகுப்பாய்வைப் பற்றி அதிகம் புரியாத பார்வையாளர்களுக்கு, குறிப்பு தெளிவாக இருப்பதாக நான் நினைக்கிறேன் ;-) ...நிறுத்து, நிறுத்து, எங்கே போகிறாய்? வரம்புகள் எளிதானது!

ஆரம்ப செயல்பாடுகளின் வரைபடங்கள் பற்றிய முதல் பாடத்தில் அறிகுறிகளின் எடுத்துக்காட்டுகள் உடனடியாகக் காணப்பட்டன, இப்போது தலைப்பு விரிவான பரிசீலனையைப் பெறுகிறது.

கற்பனை செய்து பாருங்கள் மாறி புள்ளி, இது செயல்பாட்டின் வரைபடத்தில் "பயணம்" செய்கிறது. அசிம்டோட் என்பது ஒரு நேர் கோடு காலவரையின்றி நெருக்கமாகஒரு செயல்பாட்டின் வரைபடம் அதன் மாறி புள்ளி முடிவிலிக்கு நகரும் போது நெருங்குகிறது.

குறிப்பு : குறியீட்டில் உருவாக்கம் தேவைப்பட்டால் வரையறை அர்த்தமுள்ளதாக இருக்கும் கணித பகுப்பாய்வு, டுடோரியலைப் பார்க்கவும்.

விமானத்தில், அறிகுறிகள் அவற்றின் இயற்கையான இருப்பிடத்தின் படி வகைப்படுத்தப்படுகின்றன:

1) படிவத்தின் சமன்பாட்டின் மூலம் கொடுக்கப்படும் செங்குத்து அசிம்ப்டோட்கள், "ஆல்ஃபா" என்பது ஒரு உண்மையான எண்ணாகும். ஒரு பிரபலமான பிரதிநிதி ஆர்டினேட் அச்சையே வரையறுக்கிறார்,
ஒரு சிறிய குமட்டல் உணர்வுடன் நாம் மிகைப்படுத்தலை நினைவில் கொள்கிறோம்.

2) சாய்ந்த அசிம்டோட்கள் பாரம்பரியமாக கோணக் குணகத்துடன் ஒரு நேர் கோட்டின் சமன்பாட்டால் எழுதப்படுகின்றன. சில நேரங்களில் ஒரு தனி குழு அடையாளம் காணப்படுகிறது சிறப்பு வழக்கு- கிடைமட்ட அறிகுறிகள். எடுத்துக்காட்டாக, அறிகுறியற்ற அதே ஹைப்பர்போலா.

விரைவாகச் செல்வோம், இயந்திரத் துப்பாக்கிச் சூட்டின் ஒரு சிறிய வெடிப்புடன் தலைப்பைத் தாக்குவோம்:

ஒன்று, ஒன்று, இரண்டு, மூன்று,... அல்லது எண்ணற்ற பல. எடுத்துக்காட்டுகளுக்கு நாங்கள் வெகுதூரம் செல்ல மாட்டோம், அடிப்படை செயல்பாடுகளை நினைவில் கொள்வோம். ஒரு பரவளையம், ஒரு கன பரவளையம் மற்றும் ஒரு சைன் அலை ஆகியவை அறிகுறிகளைக் கொண்டிருக்கவில்லை. அதிவேக வரைபடம், மடக்கை செயல்பாடுஒரு தனித்துவமான அறிகுறி உள்ளது. ஆர்க்டேன்ஜென்ட் மற்றும் ஆர்க்கோடேன்ஜென்ட் ஆகியவற்றில் இரண்டு உள்ளன, மேலும் டேன்ஜென்ட் மற்றும் கோடேன்ஜென்ட் ஆகியவை எண்ணற்ற பலவைக் கொண்டுள்ளன. ஒரு வரைபடமானது கிடைமட்ட மற்றும் செங்குத்து அறிகுறிகளைக் கொண்டிருப்பது அசாதாரணமானது அல்ல. ஹைப்பர்போல், எப்போதும் உன்னை நேசிப்பேன்.

ஒரு செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறிகள் வரைபடத்தின் செங்குத்து அசிம்ப்டோட், ஒரு விதியாக, செயல்பாட்டின் எல்லையற்ற இடைநிறுத்தத்தின் புள்ளியில் அமைந்துள்ளது. இது எளிமையானது: ஒரு செயல்பாட்டில் ஒரு புள்ளியில் முடிவிலா இடைநிறுத்தம் இருந்தால், நேர் கோடுசமன்பாடு மூலம் கொடுக்கப்பட்டது

குறிப்பு : உள்ளீடு இரண்டு முற்றிலும் மாறுபட்ட கருத்துகளைக் குறிக்கப் பயன்படுகிறது என்பதை நினைவில் கொள்க. ஒரு புள்ளி குறிக்கப்படுகிறதா அல்லது ஒரு கோட்டின் சமன்பாடு சூழலைப் பொறுத்தது.

எனவே, ஒரு கட்டத்தில் ஒரு செங்குத்து அறிகுறியின் இருப்பை நிறுவ, குறைந்தபட்சம் ஒரு பக்க வரம்புகளைக் காட்டினால் போதும். எல்லையற்ற. பெரும்பாலும் இது செயல்பாட்டின் வகுத்தல் பூஜ்ஜியமாக இருக்கும் புள்ளியாகும். அடிப்படையில், ஒரு செயல்பாட்டின் தொடர்ச்சி குறித்த பாடத்தின் கடைசி எடுத்துக்காட்டுகளில் செங்குத்து அறிகுறிகளை நாங்கள் ஏற்கனவே கண்டறிந்துள்ளோம். ஆனால் சில சந்தர்ப்பங்களில் ஒரே ஒரு பக்க வரம்பு உள்ளது, அது எல்லையற்றதாக இருந்தால், மீண்டும் - அன்பு மற்றும் செங்குத்து அறிகுறிகளை ஆதரிக்கவும். எளிமையான விளக்கம்: மற்றும் ஆர்டினேட் அச்சு (எலிமெண்டரி செயல்பாடுகளின் வரைபடங்கள் மற்றும் பண்புகளைப் பார்க்கவும்).

மேலே இருந்து, ஒரு வெளிப்படையான உண்மையும் பின்வருமாறு: செயல்பாடு தொடர்ந்து இருந்தால், செங்குத்து அறிகுறிகள் எதுவும் இல்லை. சில காரணங்களால் ஒரு பரவளைய நினைவு வந்தது. உண்மையில், நீங்கள் இங்கே ஒரு நேர்கோட்டை எங்கே "ஒட்டு" முடியும்? ...ஆமாம்... எனக்குப் புரிகிறது... மாமா ஃப்ராய்டைப் பின்பற்றுபவர்கள் வெறிபிடித்தார்கள் =)

உரையாடல் அறிக்கை பொதுவாக தவறானது: எடுத்துக்காட்டாக, செயல்பாடு முழு எண் கோட்டில் வரையறுக்கப்படவில்லை, ஆனால் முற்றிலும் அறிகுறியற்றது.

செயல்பாட்டின் வாதம் “பிளஸ் இன்ஃபினிட்டி” அல்லது “மைனஸ் இன்ஃபினிட்டி” என இருந்தால் சாய்ந்த (சிறப்பு நிகழ்வாக - கிடைமட்டமாக) அறிகுறிகளை வரையலாம். எனவே, ஒரு செயல்பாட்டின் வரைபடம் இரண்டுக்கு மேல் சாய்ந்த அறிகுறிகளைக் கொண்டிருக்க முடியாது. எடுத்துக்காட்டாக, ஒரு அதிவேகச் செயல்பாட்டின் வரைபடம், இல் ஒரு கிடைமட்ட அசிம்ப்டோட்டைக் கொண்டுள்ளது, மேலும் ஆர்க்டேன்ஜெண்டின் வரைபடம் இரண்டு அசிம்ப்டோட்களைக் கொண்டுள்ளது, மேலும் அதில் வேறுபட்டவை.

இரண்டு இடங்களிலும் உள்ள வரைபடம் ஒரு ஒற்றை சாய்ந்த அறிகுறியை அணுகும் போது, ​​"முடிவிலிகள்" பொதுவாக ஒரு நுழைவின் கீழ் இணைக்கப்படும். உதாரணமாக, ...நீங்கள் சரியாக யூகித்தீர்கள்: .

பொது கட்டைவிரல் விதி :

இரண்டு இருந்தால் இறுதிவரம்பு , பின்னர் நேர் கோடு என்பது செயல்பாட்டின் வரைபடத்தின் சாய்ந்த அறிகுறியாகும். பட்டியலிடப்பட்ட வரம்புகளில் குறைந்தபட்சம் ஒன்று எல்லையற்றதாக இருந்தால், சாய்ந்த அறிகுறி இல்லை.

குறிப்பு : "x" ஆனது "பிளஸ் இன்ஃபினிட்டி" அல்லது "மைனஸ் இன்ஃபினிட்டி" என்று மட்டும் இருந்தால் சூத்திரங்கள் செல்லுபடியாகும்.

பரவளையத்திற்கு சாய்வான அறிகுறிகள் இல்லை என்பதைக் காட்டுவோம்:

வரம்பு எல்லையற்றது, அதாவது சாய்ந்த அறிகுறி இல்லை. வரம்பை கண்டுபிடிப்பதில் கவனிக்கவும் பதில் ஏற்கனவே பெறப்பட்டதால் தேவை மறைந்துவிட்டது.

குறிப்பு : பிளஸ்-மைனஸ், மைனஸ்-பிளஸ் அறிகுறிகளைப் புரிந்துகொள்வதில் உங்களுக்கு (அல்லது இருந்தால்) சிரமங்கள் இருந்தால், பாடத்தின் தொடக்கத்தில் உள்ள உதவியைப் பார்க்கவும்.
எல்லையற்ற செயல்பாடுகளைப் பற்றி, இந்த அறிகுறிகளை எவ்வாறு சரியாக விளக்குவது என்பது பற்றி நான் பேசினேன்.

வெளிப்படையாக, எந்த இருபடிக்கும், கன செயல்பாடு, பல்லுறுப்புக்கோவை 4வது மற்றும் உயர் பட்டங்கள்சாய்ந்த அறிகுறிகளும் இல்லை.

இப்போது வரைபடத்தில் சாய்ந்த அறிகுறி இல்லை என்பதை உறுதி செய்வோம். நிச்சயமற்ற தன்மையை வெளிப்படுத்த, L'Hopital's விதியைப் பயன்படுத்துகிறோம்:
, இது சரிபார்க்கப்பட வேண்டியிருந்தது.

செயல்பாடு காலவரையின்றி வளரும் போது, ​​ஆனால் அதன் வரைபடம் அணுகும் நேர்கோடு இல்லை எல்லையற்ற நெருக்கமான.

பாடத்தின் நடைமுறை பகுதிக்கு செல்லலாம்:

வழக்கமான பணி எவ்வாறு வடிவமைக்கப்பட்டுள்ளது, மேலும் இது வரைபடத்தின் அனைத்து அறிகுறிகளையும் (செங்குத்து, சாய்ந்த / கிடைமட்ட) கண்டறிவதை உள்ளடக்கியது. இருப்பினும், கேள்வியை முன்வைப்பதில் மிகவும் துல்லியமாக இருக்க, நாங்கள் அறிகுறிகளின் இருப்புக்கான ஆராய்ச்சியைப் பற்றி பேசுகிறோம் (எல்லாவற்றிற்கும் மேலாக, எதுவும் இல்லை). எளிமையான ஒன்றைத் தொடங்குவோம்:

எடுத்துக்காட்டு 1

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

தீர்வு வசதியாக இரண்டு புள்ளிகளாக பிரிக்கலாம்:

1) முதலில் செங்குத்து அசிம்ப்டோட்கள் உள்ளதா என்பதைச் சரிபார்க்கிறோம். வகுத்தல் பூஜ்ஜியத்திற்கு செல்கிறது, இந்த கட்டத்தில் செயல்பாடு ஒரு முடிவிலா இடைநிறுத்தத்தை அனுபவிக்கிறது என்பது உடனடியாக தெளிவாகிறது, மேலும் சமன்பாட்டால் குறிப்பிடப்பட்ட நேர்கோடு செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறியாகும். ஆனால், அத்தகைய முடிவை எடுப்பதற்கு முன், ஒருதலைப்பட்ச வரம்புகளைக் கண்டறிவது அவசியம்:

ஒரு செயல்பாட்டின் தொடர்ச்சி கட்டுரையில் நான் இதேபோல் கவனம் செலுத்திய கணக்கீட்டு நுட்பத்தை உங்களுக்கு நினைவூட்டுகிறேன். முறிவு புள்ளிகள். வரம்பு அடையாளத்தின் கீழ் உள்ள வெளிப்பாட்டில் நாம் மாற்றியமைக்கிறோம். எண்ணிக்கையில் சுவாரஸ்யமான எதுவும் இல்லை:
.

ஆனால் வகுப்பில் அது மாறிவிடும் எல்லையற்ற எதிர்மறை எண் :
, இது வரம்பின் விதியை தீர்மானிக்கிறது.

இடது கை வரம்பு எல்லையற்றது, மேலும், கொள்கையளவில், செங்குத்து அசிம்ப்டோட் இருப்பதைப் பற்றி ஏற்கனவே தீர்ப்பளிக்க முடியும். ஆனால் ஒரு பக்க வரம்புகள் இதற்கு மட்டுமல்ல - அவை ஒரு செயல்பாட்டின் வரைபடம் எவ்வாறு அமைந்துள்ளது என்பதைப் புரிந்துகொள்வதற்கும் அதைச் சரியாகக் கட்டமைப்பதற்கும் உதவுகின்றன. எனவே, நாம் வலது கை வரம்பையும் கணக்கிட வேண்டும்:

முடிவு: ஒரு பக்க வரம்புகள் எல்லையற்றவை, அதாவது நேராக கோடு என்பது செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறியாகும்.

முதல் வரம்பு வரையறுக்கப்பட்ட, அதாவது "உரையாடலைத் தொடர" மற்றும் இரண்டாவது வரம்பைக் கண்டறிவது அவசியம்:

இரண்டாவது வரம்பும் கூட வரையறுக்கப்பட்ட.

எனவே, எங்கள் அறிகுறி:

முடிவு: சமன்பாட்டால் குறிப்பிடப்பட்ட நேர்கோடு, செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

இருந்தால் வரையறுக்கப்பட்டவரம்பு, பின்னர் நேர் கோடு என்பது செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

செயல்பாட்டின் எண் மற்றும் வகுத்தல் வளர்ச்சியின் ஒரே வரிசையில் இருப்பதைக் கவனிப்பது எளிது, அதாவது தேடப்பட்ட வரம்பு வரையறுக்கப்பட்டதாக இருக்கும்:

பதில்:

நிபந்தனையின் படி, ஒரு வரைபடத்தை உருவாக்க வேண்டிய அவசியமில்லை, ஆனால் நாம் ஒரு செயல்பாட்டை ஆராய்ச்சி செய்வதில் இருந்தால், உடனடியாக வரைவில் ஒரு ஓவியத்தை உருவாக்குகிறோம்:

கண்டுபிடிக்கப்பட்ட மூன்று வரம்புகளின் அடிப்படையில், செயல்பாட்டின் வரைபடம் எவ்வாறு அமைந்திருக்கும் என்பதை நீங்களே கண்டுபிடிக்க முயற்சிக்கவும். இது மிகவும் கடினமானதா? 5-6-7-8 புள்ளிகளைக் கண்டறிந்து அவற்றை வரைபடத்தில் குறிக்கவும். இருப்பினும், இந்த செயல்பாட்டின் வரைபடம் ஒரு அடிப்படை செயல்பாட்டின் வரைபடத்தின் மாற்றங்களைப் பயன்படுத்தி கட்டமைக்கப்பட்டுள்ளது, மேலும் மேலே உள்ள கட்டுரையின் எடுத்துக்காட்டு 21 ஐ கவனமாக ஆய்வு செய்த வாசகர்கள் இது என்ன வகையான வளைவு என்பதை எளிதாக யூகிக்க முடியும்.

எடுத்துக்காட்டு 2

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

என்பதற்கு இது ஒரு உதாரணம் சுதந்திரமான முடிவு. செயல்முறையை இரண்டு புள்ளிகளாகப் பிரிப்பது வசதியானது என்பதை நான் உங்களுக்கு நினைவூட்டுகிறேன் - செங்குத்து அறிகுறிகளும் சாய்ந்த அறிகுறிகளும். மாதிரி கரைசலில், கிடைமட்ட அசிம்ப்டோட் ஒரு எளிமையான திட்டத்தைப் பயன்படுத்தி காணப்படுகிறது.

நடைமுறையில், பகுதியளவு-பகுத்தறிவு செயல்பாடுகள் பெரும்பாலும் சந்திக்கப்படுகின்றன, மேலும் ஹைபர்போலாக்களைப் பற்றிய பயிற்சிக்குப் பிறகு, பணியை சிக்கலாக்குவோம்:

எடுத்துக்காட்டு 3

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

தீர்வு: ஒன்று, இரண்டு மற்றும் முடிந்தது:

1) செங்குத்து அசிம்டோட்கள் முடிவிலா இடைநிறுத்தத்தின் புள்ளிகளில் உள்ளன, எனவே வகுத்தல் பூஜ்ஜியத்திற்கு செல்கிறதா என்பதை நீங்கள் சரிபார்க்க வேண்டும். இருபடிச் சமன்பாட்டைத் தீர்ப்போம்:

பாகுபாடு நேர்மறையாக உள்ளது, எனவே சமன்பாடு இரண்டு உண்மையான வேர்களைக் கொண்டுள்ளது, மேலும் வேலை கணிசமாக அதிகரிக்கிறது =)

ஒரு பக்க வரம்புகளை மேலும் கண்டறிய, சதுர முக்கோணத்தை காரணியாக்குவது வசதியானது:
(சிறிய குறிப்பிற்கு, "கழித்தல்" முதல் அடைப்புக்குறிக்குள் சேர்க்கப்பட்டுள்ளது). பாதுகாப்பான பக்கத்தில் இருக்க, அடைப்புக்குறிகளை மனரீதியாக அல்லது வரைவில் திறப்பதன் மூலம் சரிபார்க்கலாம்.

படிவத்தில் செயல்பாட்டை மீண்டும் எழுதுவோம்

புள்ளியில் ஒருபக்க வரம்புகளைக் கண்டுபிடிப்போம்:

மற்றும் புள்ளியில்:

எனவே, நேர்கோடுகள் கேள்விக்குரிய செயல்பாட்டின் வரைபடத்தின் செங்குத்து அறிகுறிகளாகும்.

2) நீங்கள் செயல்பாட்டைப் பார்த்தால் , பின்னர் வரம்பு வரையறுக்கப்பட்டதாக இருக்கும் என்பதும், எங்களிடம் கிடைமட்ட அறிகுறி இருப்பதும் மிகவும் தெளிவாக உள்ளது. அதன் இருப்பைக் குறுகிய வழியில் காண்பிப்போம்:

எனவே, நேர்கோடு (abscissa axis) என்பது இந்த செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

பதில்:

கண்டறியப்பட்ட வரம்புகள் மற்றும் அறிகுறிகள் செயல்பாட்டின் வரைபடத்தைப் பற்றிய பல தகவல்களை வழங்குகின்றன. பின்வரும் உண்மைகளை கணக்கில் எடுத்துக்கொண்டு வரைபடத்தை மனதளவில் கற்பனை செய்ய முயற்சிக்கவும்:

வரைபடத்தின் உங்கள் பதிப்பை உங்கள் வரைவில் வரையவும்.

நிச்சயமாக, கண்டுபிடிக்கப்பட்ட வரம்புகள் வரைபடத்தின் தோற்றத்தை தெளிவாகத் தீர்மானிக்கவில்லை, மேலும் நீங்கள் தவறு செய்யலாம், ஆனால் செயல்பாட்டின் முழுமையான ஆய்வின் போது உடற்பயிற்சியே விலைமதிப்பற்ற உதவியை வழங்கும். சரியான படம் பாடத்தின் முடிவில் உள்ளது.

எடுத்துக்காட்டு 4

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

எடுத்துக்காட்டு 5

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

இவை சுயாதீன தீர்வுக்கான பணிகள். இரண்டு வரைபடங்களும் மீண்டும் கிடைமட்ட அறிகுறிகளைக் கொண்டுள்ளன, அவை பின்வரும் அம்சங்களால் உடனடியாகக் கண்டறியப்படுகின்றன: எடுத்துக்காட்டு 4 இல், வகுப்பின் வளர்ச்சியின் வரிசை மேலும், எண்ணின் வளர்ச்சியின் வரிசையை விட, மற்றும் எடுத்துக்காட்டு 5 இல் எண் மற்றும் வகுப்பின் வளர்ச்சியின் அதே வரிசையில் உள்ளன. மாதிரி தீர்வு, முதல் செயல்பாடு முழுமையாக சாய்ந்த அறிகுறிகளின் முன்னிலையில் ஆய்வு செய்யப்படுகிறது, மற்றும் இரண்டாவது - வரம்பு வழியாக.

கிடைமட்ட அறிகுறிகள், எனது அகநிலை உணர்வில், "உண்மையில் சாய்ந்தவை" என்பதை விட மிகவும் பொதுவானவை. நீண்டகாலமாக எதிர்பார்க்கப்பட்ட பொது வழக்கு:

எடுத்துக்காட்டு 6

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

தீர்வு: வகையின் கிளாசிக்:

1) வகுத்தல் நேர்மறையாக இருப்பதால், செயல்பாடு முழு எண் கோட்டிலும் தொடர்ச்சியாக இருக்கும், மேலும் செங்குத்து அறிகுறிகளும் இல்லை. ...இது நல்லதா? சரியான வார்த்தை இல்லை - சிறந்தது! புள்ளி எண் 1 மூடப்பட்டுள்ளது.

2) சாய்ந்த அறிகுறிகளின் இருப்பை சரிபார்க்கவும்:

முதல் வரம்பு வரையறுக்கப்பட்ட, எனவே தொடரலாம். "முடிவிலி கழித்தல் முடிவிலி" என்ற நிச்சயமற்ற நிலையை அகற்ற இரண்டாவது வரம்பைக் கணக்கிடும்போது, ​​வெளிப்பாட்டை ஒரு பொதுவான வகுப்பிற்குக் குறைக்கிறோம்:

இரண்டாவது வரம்பும் கூட வரையறுக்கப்பட்ட, எனவே, கேள்விக்குரிய செயல்பாட்டின் வரைபடம் ஒரு சாய்ந்த அறிகுறியைக் கொண்டுள்ளது:

முடிவு:

இவ்வாறு, செயல்பாட்டின் வரைபடம் போது எல்லையற்ற நெருக்கமானநேர்கோட்டை நெருங்குகிறது:

இது தோற்றத்தில் அதன் சாய்ந்த அறிகுறிகளை வெட்டுகிறது என்பதை நினைவில் கொள்க, மேலும் அத்தகைய குறுக்குவெட்டு புள்ளிகள் மிகவும் ஏற்றுக்கொள்ளத்தக்கவை - முடிவிலியில் "எல்லாம் இயல்பானது" என்பது முக்கியம் (உண்மையில், நாம் அறிகுறிகளைப் பற்றி பேசுகிறோம்).

எடுத்துக்காட்டு 7

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

தீர்வு: கருத்துத் தெரிவிக்க சிறப்பு எதுவும் இல்லை, எனவே இறுதி தீர்வின் தோராயமான உதாரணத்தை நான் வரைகிறேன்:

1) செங்குத்து அறிகுறிகள். புள்ளியை ஆராய்வோம்.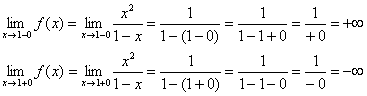

நேராக கோடு என்பது வரைபடத்திற்கான செங்குத்து அறிகுறியாகும்.

2) சாய்ந்த அறிகுறிகள்:

நேர்கோடு என்பது வரைபடத்திற்கான சாய்வான அறிகுறியாகும்.

பதில்:

கண்டுபிடிக்கப்பட்ட ஒரு பக்க வரம்புகள் மற்றும் அறிகுறிகள் இந்த செயல்பாட்டின் வரைபடம் எப்படி இருக்கும் என்பதை அதிக நம்பிக்கையுடன் கணிக்க அனுமதிக்கிறது. பாடத்தின் முடிவில் சரியான வரைதல்.

எடுத்துக்காட்டு 8

ஒரு செயல்பாட்டின் வரைபடத்தின் அறிகுறிகளைக் கண்டறியவும்

சில வரம்புகளைக் கணக்கிடுவதற்கான வசதிக்காக இது ஒரு சுயாதீனமான தீர்வுக்கான உதாரணம், நீங்கள் காலத்தின்படி வகுத்தல் காலத்தால் வகுக்க முடியும். மீண்டும், உங்கள் முடிவுகளை பகுப்பாய்வு செய்யும் போது, ​​இந்த செயல்பாட்டின் வரைபடத்தை வரைய முயற்சிக்கவும்.

வெளிப்படையாக, "உண்மையான" சாய்ந்த அறிகுறிகளின் உரிமையாளர்கள் அவற்றின் வரைபடங்கள். பகுதியளவு பகுத்தறிவு செயல்பாடுகள், இதில் எண்ணின் உயர்ந்த பட்டம் வகுப்பின் மிக உயர்ந்த பட்டத்தை விட ஒன்று அதிகமாகும். அது அதிகமாக இருந்தால், சாய்ந்த அறிகுறி இருக்காது (உதாரணமாக, ).

ஆனால் வாழ்க்கையில் மற்ற அற்புதங்கள் நடக்கின்றன:

எடுத்துக்காட்டு 9

எடுத்துக்காட்டு 11

அறிகுறிகளின் இருப்புக்கான செயல்பாட்டின் வரைபடத்தை ஆராயவும்

தீர்வு: வெளிப்படையாக , எனவே செயல்பாட்டின் வரைபடம் இருக்கும் சரியான அரை-தளத்தை மட்டுமே நாங்கள் கருதுகிறோம்.

எனவே, நேர்கோடு (ஆர்டினேட் அச்சு) என்பது செயல்பாட்டின் வரைபடத்திற்கான செங்குத்து அறிகுறியாகும்.

2) சாய்ந்த அறிகுறியற்ற தன்மை பற்றிய ஆய்வு முழு திட்டத்தின் படி மேற்கொள்ளப்படலாம், ஆனால் L'Hopital's Rules என்ற கட்டுரையில் நாங்கள் கண்டறிந்தோம் நேரியல் செயல்பாடுமடக்கையை விட அதிக வளர்ச்சி வரிசை, எனவே: (அதே பாடத்தின் எடுத்துக்காட்டு 1 ஐப் பார்க்கவும்).

முடிவு: x-அச்சு என்பது செயல்பாட்டின் வரைபடத்தின் கிடைமட்ட அறிகுறியாகும்.

பதில்:
, என்றால்;
, என்றால்.

தெளிவுக்காக வரைதல்:

வெளித்தோற்றத்தில் ஒரே மாதிரியான செயல்பாட்டிற்கு எந்த அறிகுறிகளும் இல்லை என்பது சுவாரஸ்யமானது (விரும்புபவர்கள் இதை சரிபார்க்கலாம்).

சுய ஆய்வுக்கான இரண்டு இறுதி எடுத்துக்காட்டுகள்:

எடுத்துக்காட்டு 12

அறிகுறிகளின் இருப்புக்கான செயல்பாட்டின் வரைபடத்தை ஆராயவும்