Мода случайной величины формула. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
Мода - значение во множестве наблюдений, которое встречается наиболее часто
Мо = X Mо + h Мо * (f Мо - f Мо-1) : ((f Мо - f Мо-1) + (f Мо - f Мо+1)),
здесь X Mо - левая граница модального интервала, h Мо - длина модального интервала, f Мо-1 - частота премодального интервала, f Мо - частота модального интервала, f Мо+1 - частота послемодального интервала.
Модой абсолютно непрерывного распределения называют любую точку локального максимума плотности распределения. Для дискретных распределений модой считают любое значение a i , вероятность которого p i больше, чем вероятности соседних значений
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме , т.е.
М е =(n+1) /2 Р(Х < Ме) = Р(X > Ме )
Равномерно распределенная НСВ
Равномерное распределение. Непрерывная случайная величина называется равномерно распределенной на отрезке (), если ее функция плотности распределения (рис. 1.6,а ) имеет вид :
Обозначение: – СВ распределена равномерно на .
Соответственно функция распределения на отрезке (рис. 1.6, б ):
![]()
Рис. 1.6. Функции случайной величины, распределенной равномерно на [a ,b ]: а – плотности вероятностей f (x ); б – распределения F (x )
Математическое ожидание и дисперсия данной СВ определяются выражениями:
В силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет
Пример 4. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.
27.Нормальный закон распределения вероятностей
Непрерывная случайная величина x имеет нормальльное распределение с параметрами: m,s > 0, если плотность распределения вероятностей имеет вид:
где: m – математическое ожидание, s– среднеквадратическое отклонение.
Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса . Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, , обозначают так: N (m,s), где: m=a=M[X];
Достаточно часто в формулах математическое ожидание обозначают через а . Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:
График плотности нормального распределения, который называют нормальной кривой или кривой Гаусса, изображен на рис.5.4.
Рис. 5.4. Плотность нормального распределения
свойства случайной величины, имеющей нормальный закон распределения.
1. Если , то для нахождения вероятности попадания этой величины в заданный интервал (х 1 ;х 2 ) используется формула:
2. Вероятность того, что отклонение случайной величины от ее математического ожидания не превысит величину (по абсолютной величине), равна.
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):
 (6б
)
(6б
)
Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
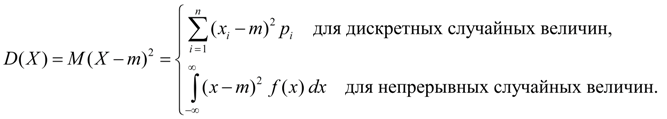 (9)
(9)
Здесь m = М (Х ).
Свойства дисперсии:
Среднее квадратичное отклонение:
![]() (11)
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:
![]() (12)
(12)
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
![]() (13)
(13)
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
![]() (14)
(14)
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С
ее центр распределения сдвигается на то же значение С
, а отклонение от центра не меняется: Х
– m
= (Х
– С
) – (m
– С
).
Теперь очевидно, что дисперсия
– это центральный момент второго порядка
:
Асимметрия. Центральный момент третьего порядка:
![]() (17)
(17)
служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :
 (18)
(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
![]() (19)
(19)
служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:
 (20)
(20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода
дискретной
случайной величины – это ее наиболее вероятное значение. Модой
непрерывной
случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным
. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным
. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными
. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального
, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.
Мода () непрерывной случайной величины – это такое ее значение, которому соответствует максимальное значение ее плотности вероятности.
Медианой () непрерывной случайной величины называется такое ее значение, которое определяется равенством:
В15. Биномиальный закон распределения и его числовые характеристики . Биномиальное распределение описывает повторяющиеся независимые опыты. Этот закон определяет появление события раз при независимых испытаниях, если вероятность появления события в каждом из этих опытов не изменяется от опыта к опыту. Вероятность:
![]() ,
,
где: – известная вероятность появления события в опыте, не изменяющаяся от опыта к опыту;
– вероятность непоявления события в опыте;
![]() – заданное число появления события в опытах;
– заданное число появления события в опытах;
![]() – число сочетаний из элементов по .
– число сочетаний из элементов по .
В15. Равномерный закон распределения, графики функции и плотности распределения, числовые характеристики . Непрерывная случайная величина считается равномерно распределенной , если ее плотность вероятности имеет вид:

Математическое ожидание случайной величины, имеющей равномерное распределение:
Дисперсия может быть вычислена следующим образом:
Среднее квадратичное отклонение будет иметь вид:
![]() .
.
В17. Показательный закон распределения, графики функции и плотности распределения, числовые характеристики . Показательным распределением непрерывной случайной величины называется такое распределение, которое описывается следующим выражением для плотности вероятности:
 ,
,
где – постоянная положительная величина.
Функция распределения вероятности в этом случае имеет вид:
![]()
Математическое ожидание случайной величины, имеющей экспоненциальное распределение, получаем на основании общей формулы с учетом того, что при :
![]() .
.
Интегрируя это выражение по частям, находим: .
Дисперсию для экспоненциального распределения можно получить, используя выражение:
![]() .
.
Подставляя выражение для плотности вероятности, находим:
![]()
Вычисляя интеграл по частям, получаем: .
В16. Нормальный закон распределения, графики функции и плотности распределения. Стандартное нормальное распределение. Функция отраженного нормального распределения . Нормальным называется такое распределение случайной величины , плотность вероятности которого описывается функцией Гаусса:

где – среднее квадратичное отклонение;
– математическое ожидание случайной величины.
 |
График плотности нормального распределения называют нормальной кривой Гаусса.
В18. Неравенство Маркова. Обобщенное неравенство Чебышева
. Если для случайной величины X
существует , то для любого справедливо неравенство Маркова
![]() .
.
Оно вытекает из обобщенного неравенства Чебышева
: Пусть функция монотонно возрастает и неотрицательна на . Если для случайной величины X
существует , то для любого справедливо неравенство ![]() .
.
В19. Закон больших чисел в форме Чебышева. Его смысл. Следствие закона больших чисел в форме Чебышева. Закон больших чисел в форме Бернулли . Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт асимптотического приближения среднего значения большого числа опытных данных к математическому ожиданию случайной величины. В основе доказательств этих теорем лежит неравенство Чебышева. Это неравенство можно получить, рассматривая дискретную случайную величину, имеющую возможных значений .
Теорема. Пусть имеется конечная последовательность ![]() независимых случайных величин, с одним и тем же математическим ожиданием и дисперсиями, ограниченными одной и той же постоянной :
независимых случайных величин, с одним и тем же математическим ожиданием и дисперсиями, ограниченными одной и той же постоянной :
Тогда, каково бы ни было число , вероятность события
![]()
стремится к единице при .
Теорема Чебышева устанавливает связь между теорией вероятностей, которая рассматривает средние характеристики всего множества значений случайной величины, и математической статистикой, оперирующей ограниченным множеством значений этой величины. Она показывает, что при достаточно большом числе измерений некоторой случайной величины среднее арифметическое значений этих измерений приближается к математическому ожиданию.
В20. Предмет и задачи математической статистики. Генеральная и выборочная совокупности. Способ отбора . Математическая статистика – наука о математических методах систематизации и использования статистических данных для научных и практических выводов, опирающаяся на теорию вероятностей.
Объектами изучения математической статистики являются случайные события, величины и функции, которые характеризуют рассматриваемое случайное явление. Случайными являются следующие события: выигрыш на один билет денежной лотереи, соответствие контролируемого продукта установленным требованиям, безотказная работа автомобиля в течение первого месяца его эксплуатации, выполнение подрядчиком суточного графика работ.
Выборочной совокупностью называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
В21. Способы отбора.
Способы отбора: 1 Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся а) простой случайный бесповторный отбор и б) простой случайный повторный отбор. 2) Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся а) типический отбор, б) механический отбор и в) серийный отбор.
Простым случайным называют отбор, при котором объекты извлекаются по одному из генеральной совокупности.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части.
Механическим называют отбор, при котором генеральная совокупность механически делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы выбирается один объект.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.
В22. Статистический и вариационный ряд. Эмпирическая функция распределения и ее свойства . Вариационный ряд для дискретных и непрерывных случайных величин. Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра наблюдалось раз, - раз и т.д. При этом объем выборки. Наблюдаемые значения называют вариантами , а последовательность вариант, записанных в возрастающем порядке – вариационным рядом . Числа наблюдений называют частотами , а их отношения к объему выборки - относительными частотами . Вариационный ряд можно представить таблицей вида:
| X | ….. | |||
| n | …. |
Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:
| X | ….. | |||
| w | …. |
где относительные частоты .
Эмпирической функцией распределения
называют функцию , определяющую для каждого значения x относительную частоту события X Среди числовых
характеристик случайных величин нужно, прежде всего, отметить те, которые
характеризуют положение случайной
величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное
значение, около которого группируются все возможные значения случайной
величины. Среднее
значение случайной величины есть некоторое число, являющееся как бы её
«представителем» и заменяющее её при грубо ориентировочных расчетах. Когда мы
говорим: «среднее время работы лампы равно 100 часам» или «средняя точка
попадания смещена относительно цели на 2 м вправо», мы этим указываем определенную числовую характеристику случайной величины, описывающую её местоположение
на числовой оси, т.е. «характеристику положения». Из
характеристик положения в теории вероятностей важнейшую роль играет математическое
ожидание случайной величины, которое иногда называют просто средним
значением случайной величины. Рассмотрим дискретную
случайную величину ,
имеющую возможные значения с вероятностями . Нам требуется охарактеризовать
каким-то числом положение значений случайной величины на оси абсцисс с учетом
того, что эти значения имеют различные вероятности. Для этой цели естественно
воспользоваться так называемым «средним взвешенным» из значений , причем каждое
значение при
осреднении должно учитываться с «весом», пропорциональным вероятности этого
значения. Таким образом, мы вычислим среднее случайной величины , которое мы обозначим : или, учитывая, что , Это среднее
взвешенное значение и называется математическим ожиданием случайной величины.
Таким образом, мы ввели в рассмотрении одно из важнейших понятий теории
вероятностей – понятие математического ожидания. Математическим
ожиданием случайной величины называется сумма произведений всех возможных
значений случайной величины на вероятности этих значений. Заметим, что в
вышеприведенной формулировке определение математического ожидания справедливо,
строго говоря, только для дискретных случайных величин; ниже будет дано
обобщение этого понятия на случай непрерывных величин. Для того,
чтобы сделать понятие математического ожидания более наглядным, обратимся к
механической интерпретации распределения дискретной случайной величины. Пусть
на оси абсцисс расположены точки с абсциссами , в которых сосредоточены соответственно
массы ,
причем .
Тогда, очевидно, математическое ожидание , определяемое формулой (5.6.1), есть не
что иное, как абсцисса центра тяжести данной системы материальных точек. Математическое
ожидание случайной величины связано своеобразной зависимостью со средним арифметическим наблюденных значений
случайной величины при большом числе опытов. Эта зависимость того же типа, как
зависимость между частотой и вероятностью, а именно: при большом числе опытов
среднее арифметическое наблюденных значений случайной величины приближается
(сходится по вероятности) к ее математическому ожиданию. Из наличия связи между
частотой и вероятностью можно вывести как следствие наличие подобной же связи
между средним арифметическим и математическим ожидание. Действительно,
рассмотрим дискретную случайную величину , характеризуемую рядом распределения: где Пусть
производится независимых
опытов, в каждом из которых величина принимает определенное значение.
Предположим, что значение появилось раз, значение появилось раз, вообще значение появилось раз. Очевидно, Вычислим
среднее арифметическое наблюденных значений величины , которое, в отличие от
математического ожидания мы обозначим : Но есть не что иное, как частота (или статистическая вероятность)
события ; эту
частоту можно обозначить . Тогда т.е. среднее арифметическое
наблюденных значений случайной величины равно сумме произведений всех возможных
значений случайной величины на частоты этих значений. При увеличении
числа опытов частоты
будут
приближаться (сходиться по вероятности) к соответствующим вероятностям . Следовательно, и
среднее арифметическое наблюденных значений случайной величины при увеличении числа
опытов будет приближаться (сходится по вероятности) к её математическому
ожиданию . Сформулированная
выше связь между средним арифметическим и математическим ожиданием составляет
содержание одной из форм закона больших чисел. Строгое доказательство этого
закона будет дано нами в главе 13. Мы уже знаем,
что все формы закона больших чисел констатируют факт устойчивости некоторых
средних при большом числе опытов. Здесь речь идет об устойчивости среднего
арифметического из ряда наблюдений одной и той же величины. При небольшом числе
опытов среднее арифметическое их результатов случайно; при достаточном
увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь,
приближается к постоянной величине – математическому ожиданию. Свойство
устойчивости средних при большом числе опытов легко проверить экспериментально.
Например, взвешивая какое-либо тело в лаборатории на точных весах, мы в
результате взвешивания получаем каждый раз новое значение; чтобы уменьшить
ошибку наблюдения, мы взвешиваем тело несколько раз и пользуемся средним
арифметическим полученных значений. Легко убедиться, что при дальнейшем
увеличении числа опытов (взвешиваний) среднее арифметическое реагирует на это
увеличение все меньше и меньше и при достаточно большом числе опытов
практически перестает меняться. Формула
(5.6.1) для математического ожидания соответствует случаю дискретной случайной
величины. Для непрерывной величины математическое ожидание, естественно,
выражается уже не суммой, а интегралом: где - плотность распределения величины . Формула
(5.6.2) получается из формулы (5.6.1), если в ней заменить отдельные значения непрерывно
изменяющимся параметром х, соответствующие вероятности - элементом
вероятности ,
конечную сумму – интегралом. В дальнейшем мы часто будем пользоваться таким
способом распространения формул, выведенных для прерывных величин, на случай
непрерывных величин. В механической
интерпретации математическое ожидание непрерывной случайной величины сохраняет
тот же смысл – абсцисса центра тяжести в случае, когда масса распределена по
оси абсцисс непрерывно, с плотностью . Эта интерпретация часто позволяет найти
математическое ожидание без вычисления интеграла (5.6.2), из простых
механических соображений. Выше мы ввели
обозначение для
математического ожидания величины . В ряде случаев, когда величина входит в формулы как
определенное число, её удобнее обозначать одной буквой. В этих случаях мы будем
обозначать математическое ожидание величины через : Обозначения и для математического ожидания будут в
дальнейшем применяться параллельно в зависимости от удобства той или иной
записи формул. Условимся также в случае надобности сокращать слова
«математическое ожидание» буквами м.о. Следует
заметить, что важнейшая характеристика положения – математическое ожидание –
существует не для всех случайных величин. Можно составить примеры таких
случайных величин, для которых математического ожидания не существует, так как
соответствующая сумма или интеграл расходятся. Рассмотрим,
например, прерывную случайную величину с рядом распределения: Нетрудно
убедится в том, что ,
т.е. ряд распределения имеет смысл; однако сумма в данном случае расходится и,
следовательно, математического ожидания величины не существует. Однако для практики такие
случаи существенного интереса не представляют. Обычно случайные величины, с
которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно,
обладают математическим ожиданием. Выше мы дали
формулы (5.6.1) и (5.6.2), выражающие математическое ожидание соответственно
для прерывной и непрерывной случайной величины . Если величина принадлежит к
величинам смешанного типа, то её математическое ожидание выражается формулой
вида: где сумма распространяется на все
точки , в
которых функция распределения терпит разрыв, а интеграл – на все участки, на
которых функция распределения непрерывна. Кроме
важнейшей из характеристик положения – математического ожидания, - на практике
иногда применяются и другие характеристики положения, в частности, мода
и медиана случайной величины. Модой
случайной величины называется её наиболее вероятное значение. Термин «наиболее
вероятное значение», строго говоря, применим только к прерывным величинам; для
непрерывной величины модой является то значение, в котором плотность
вероятности максимальна. Условимся обозначать моду буквой . На рис. 5.6.1 и 5.6.2 показана
мода соответственно для прерывной и непрерывной случайных величин. Если
многоугольник распределения (кривая распределения) имеет более одного
максимума, распределение называется «полимодальным» (рис. 5.6.3 и 5.6.4). Иногда
встречаются распределения, обладающие посередине не максимумом, а минимумом
(рис. 5.6.5 и 5.6.6). Такие распределения называют «антимодальными». Примером
антимодального распределения может служить распределение, полученное в примере
5, n° 5.1. В общем случае
мода и математическое ожидание случайной величины не совпадают. В частном
случае, когда распределение является симметричным и модальным (т.е. имеет моду)
и существует математическое ожидание, то оно совпадает с модой и центром
симметрии распределения. Часто
применяется еще одна характеристика положения – так называемая медиана
случайной величины. Этой характеристикой пользуются обычно только для непрерывных
случайных величин, хотя формально можно её определить и для прерывной величины. Медианой
случайной величины называется такое её значение , для которого т.е. одинаково вероятно, окажется
ли случайная величина меньше или больше . Геометрически медиана – это абсцисса
точки, в которой площадь, ограниченная кривой распределения, делится пополам
(рис. 5.6.7).
 . (5.6.1)
. (5.6.1)
![]() .
. ,
, , (5.6.2)
, (5.6.2)
 , (5.6.3)
, (5.6.3)





